CLINS

Posted on Edited on In Waline:

关于论文 CLINS：Continuous-Time Trajectory Estimation for LiDAR-Inertial System (IROS 2021) 的阅读总结。

CLINS

0 论文简介

  • 标题：CLINS：Continuous-Time Trajectory Estimation for LiDAR-Inertial System
  • 作者：Jiajun Lv，Kewei Hu，Jinhong Xu，Yong Liu，Xiushui Ma，Xingxing Zuo
  • 会议：IROS 2021
  • 源码：https://github.com/APRIL-ZJU/clins

1 介绍

基于 discrete-time 的方法通过差值的方法将 LiDAR 点去畸变为扫描的起始时刻。IMU 数据被差值和融合来形成两个离散 scan 的相对位姿约束。但是这种方法存在一下的缺陷：

  • 在实际中，传感器之间不是以相同的频率获取测量数据，这将产生不可忽视的误差。
  • 直接使用原始 LiDAR 测量数据和 IMU 数据是困难的。原始 LiDAR 点数据需要被去畸变至特定时刻以产生 LiDAR scan，而原始 IMU 数据则用于生成相对位姿。

这些问题是由于难以处理高频传感器产生的原始数据而形成的，直接使用这些数据需要大量的位姿变量。上述问题可被归纳为离散的位姿表达无法满足系统的高分辨率要求。

目前出现了 continuous-time 的方法，通过将轨迹建模为时间的函数并支持查询任何时间戳下的位姿，解决了集成异步和高频数据的问题。CLINS 提出了一种 LiDAR 惯性系统的完全基于 continuous-time 轨迹估计框架，主要贡献如下：

  • 提出了 continuous-time 轨迹估计子（estimator），可以支持 3D LiDAR 点和惯性数据的融合，并且能容易地拓展以融合其他不同频率的异步传感器产生的数据。
  • 提出了一种两阶段的 continuous-time 轨迹修正方法来高效解决回环检测问题。

2 连续时间轨迹的表达方式

定义 6-DoF 刚性变换 ABT∈SE(3)∈R4×4{}_A^B \pmb{T} \in SE(3) \in \mathbb{R}^{4 \times 4}，将帧 {A}\{ A\} 中的点 Ap∈R3{}^A \pmb{p} \in \mathbb{R}^3 变换到帧 {B}\{ B\} 中。变换矩阵为：

ABT=[ABRBpAA01]{}_A^B \pmb{T} = \left[ \begin{matrix} {}_A^B \pmb{R} &{}^B \pmb{p}_A \\ {}^A \pmb{0} &1 \end{matrix} \right]

其中旋转部分 ABR∈SO(3){}_A^B \pmb{R} \in SO(3)，平移部分 BpA∈R3{}^B \pmb{p}_A \in \mathbb{R}^3。为简化，将变换过程写为其次方程：

Bp=ABTAp{}^B \pmb{p} = {}_A^B \pmb{T} {}^A \pmb{p}

Exp(⋅)Exp(\cdot) 函数将 R3\mathbb{R}^3 中的向量映射到李群 SO(3)SO(3)，Log(⋅)Log(\cdot) 为此映射的反过程，(⋅)∨(\cdot)_{\vee} 将李代数中的元素映射到向量。

B 样条曲线（B-spline）是光滑且局部连续的，其具有封闭形式的解析导数，使得很容易与 IMU 测量数据匹配。为此，CLINS 使用了两个分离的 B-spline 群来参数化 3D 平移和 3D 旋转，p(t)∈R3\pmb{p}(t) \in \mathbb{R}^3 和 R(t)∈SO(3)\pmb{R}(t) \in SO(3)。均匀 B 样条曲线的总结如下表：

Uniform B-Spline Basics
Order kk
Knot distance Δt\Delta t
Coeff. Vec. (1) ϕ(u)=M(k)u\phi(u) = \pmb{M}^{(k)} \pmb{u}
Cumul. Coeff. Vec. (1,2) λ(u)=M~(k)u\pmb{\lambda}(u) = \tilde{\pmb{M}}^{(k)} \pmb{u}
Position in Cumulative Form
Control point Φp=pi∈R3, i∈[0,n]\pmb{\Phi}_p = {\pmb{p}_i} \in \mathbb{R}^3,\ i \in [0,n]
Distance dji=pi+j−pi+j−1∈R3d_j^i = \pmb{p}_{i+j} - \pmb{p}_{i + j - 1} \in \mathbb{R}^3
Position p(u)=pi+∑j=1k−1λj⋅dji\pmb{p}(u) = \pmb{p}_i + \sum_{j=1}^{k-1} \lambda_j \cdot \pmb{d}_j^i
Velocity v(u)=∑j=1k−1λ˙j(u)⋅dji\pmb{v}(u) = \sum_{j=1}^{k-1} \dot{\lambda}_j(u) \cdot \pmb{d}_j^i
Acceleration a(u)=∑j=1k−1λ¨j(u)⋅dji\pmb{a}(u) = \sum_{j=1}^{k-1} \ddot{\lambda}_j(u) \cdot \pmb{d}_j^i
Orientation in Cumulative Form
Control point ΦR=Ri∈SO(3), i∈[0,n]\pmb{\Phi}_R = {\pmb{R}_i} \in SO(3),\ i \in [0,n]
Distance dji=Log(Ri+j−1−1Ri+j)∈R3d_j^i = Log(\pmb{R}_{i+j-1}^{-1} \pmb{R}_{i+j}) \in \mathbb{R}^3
Position R(u)=Ri⋅∏j=1k−1Exp(λj(u)⋅dji)\pmb{R}(u) = \pmb{R}_i \cdot \prod_{j=1}^{k-1} Exp(\lambda_j(u) \cdot \pmb{d}_j^i)
Velocity ω(u)=(R⊤R˙)∨\pmb{\omega}(u) = (\pmb{R}^\top \dot{\pmb{R}})_{\vee}

其中：

  • (1) t∈[ti,ti+1), u(t)=s(t)−i,s(t)=(t−t0)/Δtt \in [t_i, t_{i+1}),\ u(t) = s(t) - i, s(t) = (t - t_0) / \Delta t
  • (2) 注意 λ0(u)≡1\lambda_0(u) \equiv 1

特别的，样条矩阵 M(k)M^{(k)} 和累积矩阵 M~(k)\tilde{M}^{(k)} 对于 B 样条曲线来说是常量。对于 Rn\mathbb{R}^n 中的平移轨迹，B 样条曲线的基本形式和累积形式是等价可相互转换的，而在非欧氏空间 SO(3)SO(3) 中这是不成立的。旋转轨迹可以使用累积形式表示，上表列出了 R3\mathbb{R}^3 和 SO(3)SO(3) 中的累积形式。取样条曲线对时间的倒数，可以得到速度和加速度。上表中的线速度 v(t)\pmb{v}(t) 和线加速度 a(t)\pmb{a}(t) 是在全局坐标系中的，而角速度 ω(t)\pmb{\omega}(t) 则在局部坐标系。

全局坐标系 {G}\{G\} 下 IMU 的 continuous-time 轨迹变换为：

IGT(t)=[R(t)p(t)01]{}_I^G \pmb{T}(t) = \left[ \begin{matrix} \pmb{R}(t) &\pmb{p}(t) \\ \pmb{0} &1 \end{matrix} \right]

由于已知 IMU 和 LiDAR 之间的变换（外参）LIT{}_L^I \pmb{T}，因此 LiDAR 的轨迹变换为：

LGT(t)=IGT(t)LIT{}_L^G \pmb{T}(t) = {}_I^G \pmb{T}(t) {}_L^I \pmb{T}

由于 B 样条曲线的局部性，对于 t∈[ti,ti+1)t \in [t_i, t_{i+1})，IGT{}_I^G \pmb{T} 只受到 {ti,ti+1,⋯ ,ti+k−1}\{ t_i, t_{i+1}, \cdots, t_{i+k-1} \} 的 knots 及与其相关的 control points 集 Φ(ti,ti+1)\pmb{\Phi}(t_i, t_{i+1}) 的控制，其中：

Φ(ti,ti+1)=ΦR(ti,ti+1)∪Φp(ti,ti+1)={Ri,⋯ ,Ri+k−1}∪{pi,⋯ ,pi+k−1}\begin{aligned} \pmb{\Phi}(t_i, t_{i+1}) &= \pmb{\Phi}_R (t_i, t_{i+1}) \cup \pmb{\Phi}_p (t_i, t_{i+1}) \\ &= \{ \pmb{R}_i, \cdots, \pmb{R}_{i+k-1} \} \cup \{ \pmb{p}_i, \cdots, \pmb{p}_{i+k-1} \} \end{aligned}

3 方法

如图是所提出的 LiDAR 惯性系统 continuous-time 轨迹估计所涉及的定义。根据当前 LiDAR 扫描数据的采集时间间隔来定义 active segments。Active segments 对应的控制点序列 Φactive\pmb{\Phi}_{active} 记为活动控制点（active control points，蓝点和红点）。对应于 Φactive\pmb{\Phi}_{active} 的基函数子集表示为活动基函数（蓝色曲线和红色曲线）。Active 轨迹（蓝色和红色）是由局部区域的活动控制点决定。此外，除了 active segments 的时间，与活动基函数有关的时间段被标记为 static segments。据此定义了静态控制点 Φstatic\pmb{\Phi}_{static}（static control points，绿色点）和静态基函数（绿色曲线）。

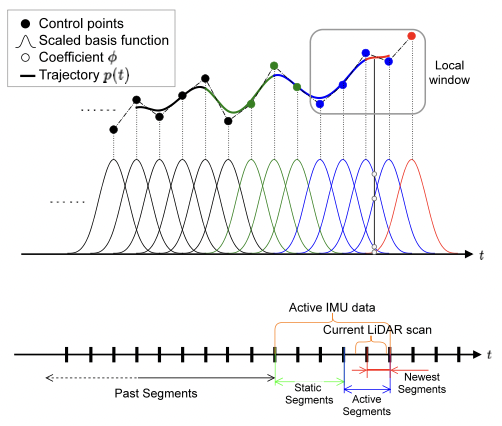
图-1 系统框架

该系统在一次新的 LiDAR 扫描后，在状态向量中加入新的控制点（红点），对扩展轨迹进行参数化。利用集成的 IMU 姿态来初始化这些新的控制点。随后，从当前扫描帧中提取边缘点和平面点等 LOAM 特征与局部子地图进行数据关联。最后，给定原始 IMU 测量在局部窗口和相关的 LiDAR 特征，使用批量优化的方式估计 continuous-time 轨迹。状态估计问题可以表述为最大后验概率（MAP）问题。基于传感器测量数据存在独立高斯噪声的假设，可以通过求解非线性最小二乘（NLLS）问题来估计 continuous-time 轨迹。

3.1 初始化

当新的 LiDAR 帧到达后，新的 control points 被加入以扩展现有的轨迹。融合离散的 IMU 数据来获取时间 tmt_m 的高频的旋转 RIm\pmb{R}_{I_m}、平移 pIm\pmb{p}_{I_m} 和线速度 vIm\pmb{v}_{I_m} 估计。可以最小化一下损失函数来初始化新加入的 control points Φnew\pmb{\Phi}_{new}：

argmin⁡Φnew∑(∣∣Log(RIm⊤)R(tm)∣∣+∣∣p(tm)−pIm∣∣+∣∣v(tm)−vIm∣∣)\underset{\pmb{\Phi}_{new}}{\operatorname{argmin}} \sum (|| Log(\pmb{R}_{I_m}^{\top}) \pmb{R}(t_m) || + || \pmb{p}(t_m) - \pmb{p}_{I_m} || + || \pmb{v}(t_m) - \pmb{v}_{I_m} ||)

3.2 局部窗口的非网格注册

对于新到来的帧 SkS_k，其在时间间隔 [tk,tk+ΔT][t_k, t_k + \Delta T]（tkt_k 为 SkS_k 中第一个点的时间戳，ΔT\Delta T 为完成一次 LiDAR 扫描的周期）收集得到，如果在扫描过程中传感器存在外部移动，那么 SkS_k 中的非网格点云就十分重要。因此传统计算两个网格点云的相对变换的注册算法，将不适用于这种点云。为解决这个问题，此处提出了一个非网格注册的方法。

特别地，SkS_k 中的每一个点变换到一个统一的坐标系 {Lk}\{ L_k \} 中：

Lkxkj=LGT(tk)⊤LGT(tk+τj)Lkjxkj{}^{L_k} \pmb{x}_{kj} = {}^G_L T(t_k)^\top {}^G_LT(t_k + \tau_j) {}^{L_{kj}} \pmb{x}_{kj}

τj\tau_j 为点 Lkjxkj{}^{L_{kj}} \pmb{x}_{kj} 相对当前帧起始时间点时间戳。为使计算易处理，通过计算曲率从原始点云中提取出面特征（planar features）和边特征（edge features）。

考虑到 LiDAR 数据在一些非结构化的环境中会退化，同时高频的 IMU 数据不受影响，因此将 IMU 测量同 LiDAR 特征紧耦合以约束轨迹。于是非网格注册问题可以被定义为：给定当前帧 active segment 和 static segment 对应的 LiDAR 特征和惯性数据，估计轨迹的活动控制点 Φ(tk,tk+ΔT)\pmb{\Phi} (t_k, t_k + \Delta T) 和 IMU 的偏差。具体地，可以通过求解下目标函数来解决这个问题：

argname⁡X∑∣∣rL∣∣ΣL+∣∣ra∣∣Σa+∣∣rw∣∣Σw\underset{\mathcal{X}}{\operatorname{argname}} \sum ||\pmb{r}_{\mathcal{L}}||_{\pmb{\Sigma}_{\mathcal{L}}} + ||\pmb{r}_a||_{\pmb{\Sigma}_{\mathcal{a}}} + ||\pmb{r}_w||_{\pmb{\Sigma}_{\mathcal{w}}}

其中 X={Φ(tk,tk+ΔT),ba,bg}\mathcal{X} = \{ \pmb{\Phi}(t_k, t_k + \Delta T), \pmb{b}_a, \pmb{b}_g \}，ba,bg\pmb{b}_a,\pmb{b}_{g} 分别表示加速度计和陀螺仪的偏差，rL,ra,rw\pmb{r}_{\mathcal{L}}, \pmb{r}_a, \pmb{r}_w 表示 LiDAR 特征和 IMU 测量的残差，ΣL,Σa,Σw\pmb{\Sigma}_{\mathcal{L}}, \pmb{\Sigma}_a, \pmb{\Sigma}_w 为响应的协方差矩阵。残差的定义如下：

rL=π(LGT(tk+τj)Lkjxkj)ra=LGR⊤(tm)(a(tm)−Gg)−am+barw=ω(tm)−ωm+bw\begin{aligned} \pmb{r}_{\mathcal{L}} &= \pi ({}^G_L T(t_k + \tau_j) {}^{L_{kj}}\pmb{x}_{kj}) \\ \pmb{r}_a &= {}_L^G \pmb{R}^\top (t_m) (\pmb{a}(t_m) - {}^G \pmb{g}) - \pmb{a}_m + \pmb{b}_a \\ \pmb{r}_w &= \pmb{\omega} (t_m) - \pmb{\omega}_m + \pmb{b}_w \end{aligned}

其中投影函数 π(⋅)\pi(\cdot) 对面特征进行点到平面投影，对边特征进行点到线投影。am,ωm\pmb{a}_m,\pmb{\omega}_m 为时间 tmt_m 的惯性测量数据。注意到静态控制点被包含在优化过程中，但在优化过程中保持不变。使用 Ceres 中的 LM 法求解上述非线性最小二乘问题。

3.3 轨迹修正

里程系统的累积漂移误差是无法避免的，本文在出现回环时进行修正以减缓累积误差。考虑到在有许多 knot 的连续轨迹上使用全局优化是费时的，因此此处提出了一个两阶段的轨迹优化方法降低时间复杂度和计算开销：

  • 第一阶段，当检测到回环时，在关键帧的离散位姿上进行位姿图优化来限制累积误差。
  • 第二阶段，使用更新过的关键帧的位姿尝试更新控制点。这个过程可以被理解为将连续的轨迹投影到某些锚位姿上并保留轨迹的局部形状。

一般来说，局部的惯导估计是准确的，因此在某一确切时刻的原始 continuous-time 轨迹上计算局部线速度和角速度。因此，第二阶段的问题可以被形式化为求解如下函数：

argname⁡Φupdate∑(∣∣Log(R^k⊤R(tk))∣∣+∣∣p(tk)−p^k∣∣)+∑(∣∣R(tj)⊤v(tj)−v^j∣∣+∣∣ω(tj)−ω^j∣∣)\underset{\pmb{\Phi}_{update}}{\operatorname{argname}} \sum (||Log(\hat{\pmb{R}}_k^\top \pmb{R}(t_k))|| + ||\pmb{p}(t_k) - \hat{\pmb{p}}_k||) + \sum (||\pmb{R}(t_j)^\top \pmb{v}(t_j) - \hat{\pmb{v}}_j|| + ||\pmb{\omega}(t_j) - \hat{\pmb{\omega}}_j||)

其中 R^k,p^k\hat{\pmb{R}}_k, \hat{\pmb{p}}_k 表示位姿优化后时间 tkt_k 更新后的关键帧的位姿，v^j,ω^j\hat{\pmb{v}}_j, \hat{\pmb{\omega}}_j 为修正前时间 tjt_j 的线速度和角速度。下Í图为两阶段方法的示意图：

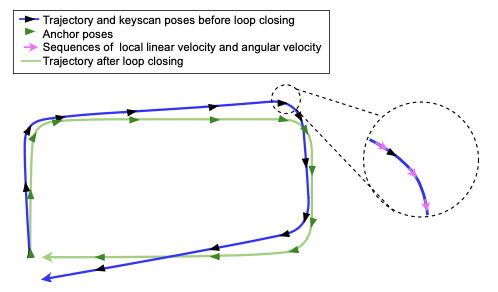
图-2 两阶段修正

4 试验结果

4.1 数据集

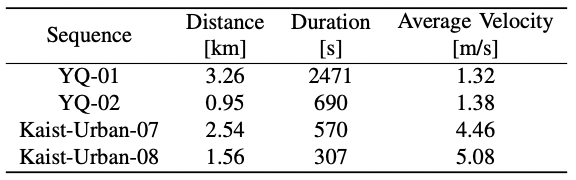
图-3 数据集

4.2 RMSE

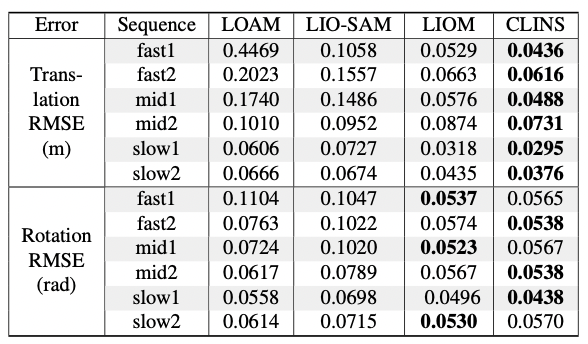
图-4 平移和旋转的 RMSE

4.3 与其他模型的对比

其中 LIO-SAM(odom) 和 CLINS(odom) 表示去除回环修正：

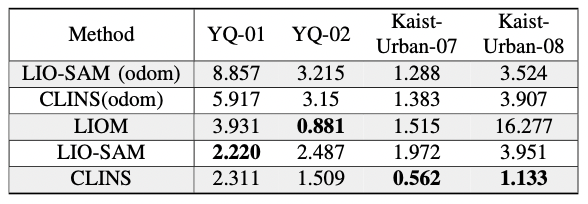
图-5 与其他模型的对比

4.4 可视化结果

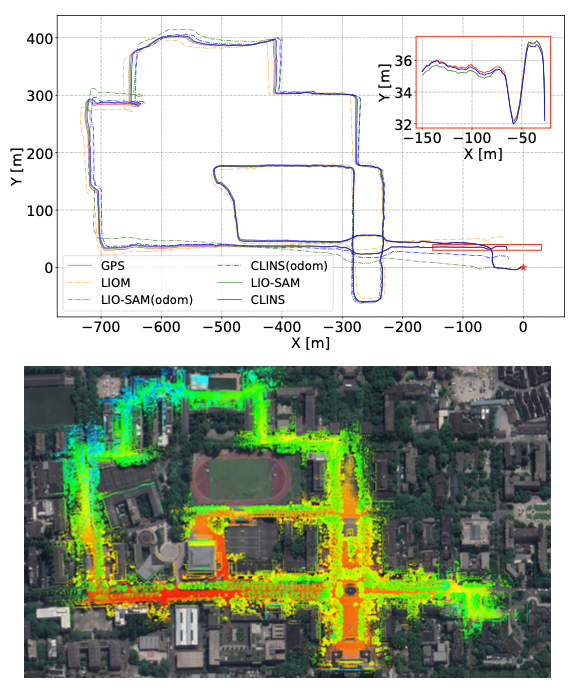
图-6 结果可视化

5 B 样条曲线

5.1 参考