关于论文 DP-SLAM: A visual SLAM with moving probability towards dynamic environments (Information Sciences, 2021) 的阅读总结。
DP-SLAM
论文情况
- 标题:DP-SLAM: A visual SLAM with moving probability towards dynamic environments
- 作者:Ao Li, Jikai Wang, Meng Xu, Zonghai Chen
- 期刊:Information Sciences, 2021
- 源码:未开源
1 Introduction
动态物体对传统静态假设的 SLAM 系统的影响:
- 运动物体容易使系统得到错误的数据关联结果,破坏视觉里程测量;
- 动态物体可能导致错误的位置识别,回环检测的性能也会下降。
前端引入目标检测能力产生的问题:
- RANSAC 用于在前端拒绝 outliers,但当移动物体占据图像的大部分时,算法往往会失败;
- 引入 CNN 进行检测,但由于训练一般是基于公共数据集,所以检测能力有限,可能会将动态点误分类为静态。
本文提出了一种将几何模型和深度学习算法相结合的动态关键点的移动概率传播模型,将运动关键点拒绝定义为运动去除(motion removal)。主要贡献为:
- 提出了一种新的运动移除方法,实时传播每个关键点的运动概率,克服了几何约束和语义信息的偏差;
- 对背景进行静态信息填充,得到无动态内容的合成 RGB 帧及对应的深度帧,有利于 VR 应用;
- 使用 TUM 数据集和 ORB-SLAM2 进行对比。
2 DP-SLAM
2.1 The Approach Overview
Fig.1 为算法的流程图,在预处理阶段,过滤掉移动对象的相关数据,从而减少 SLAM 前端不正确数据的关联。
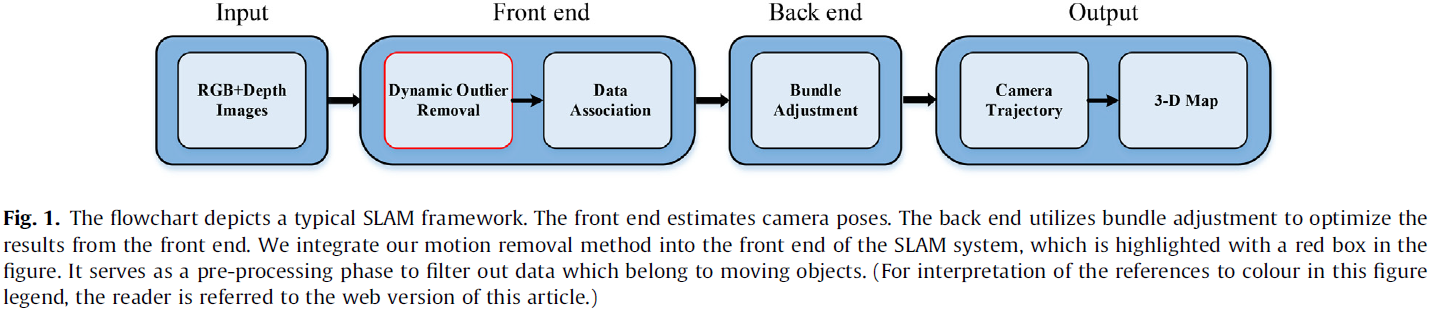
如 Fig.2,本文的方法结合几何模型和语义分割来去除运动,其结果转化为观测概率。前一帧关键点的移动概率作为先验概率,基于贝叶斯定理,可以根据观测概率和先验概率更新各个关键点的移动概率。然后剔除移动概率高(>0.5)的关键点。
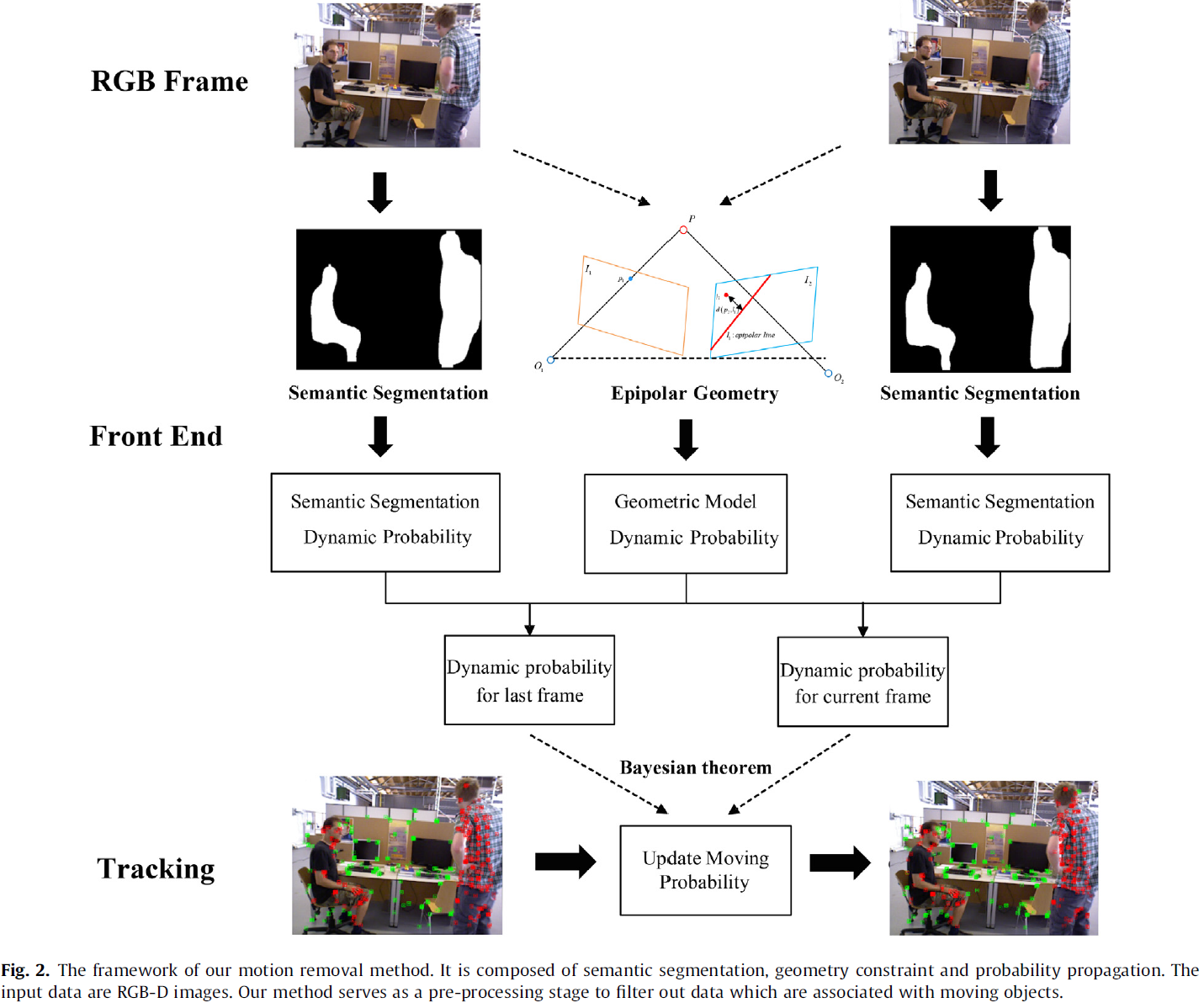
2.2 Semantic Segmentation
为实现动态物体的检测,使用 Mask R-CNN[1] 进行目标分割以及像素级的语义分割。使用 Mask R-CNN 识别的动态物体包括人、自行车、汽车、摩托车等,如果需要识别其他物体可以添加训练数据进行模型调整。Mask R-CNN 输入原始 RGB 帧,输出原始帧中每个对象的二进制掩码。
CNN 可能没有精确的分割动态对象(尤其在对象边缘),导致掩码覆盖了静态区域。为此,使用二项逻辑回归计算每个关键点的动态概率,如 Fig.3,掩码中动态概率异常(<0.75)的关键点则认为可能位于静态背景上。
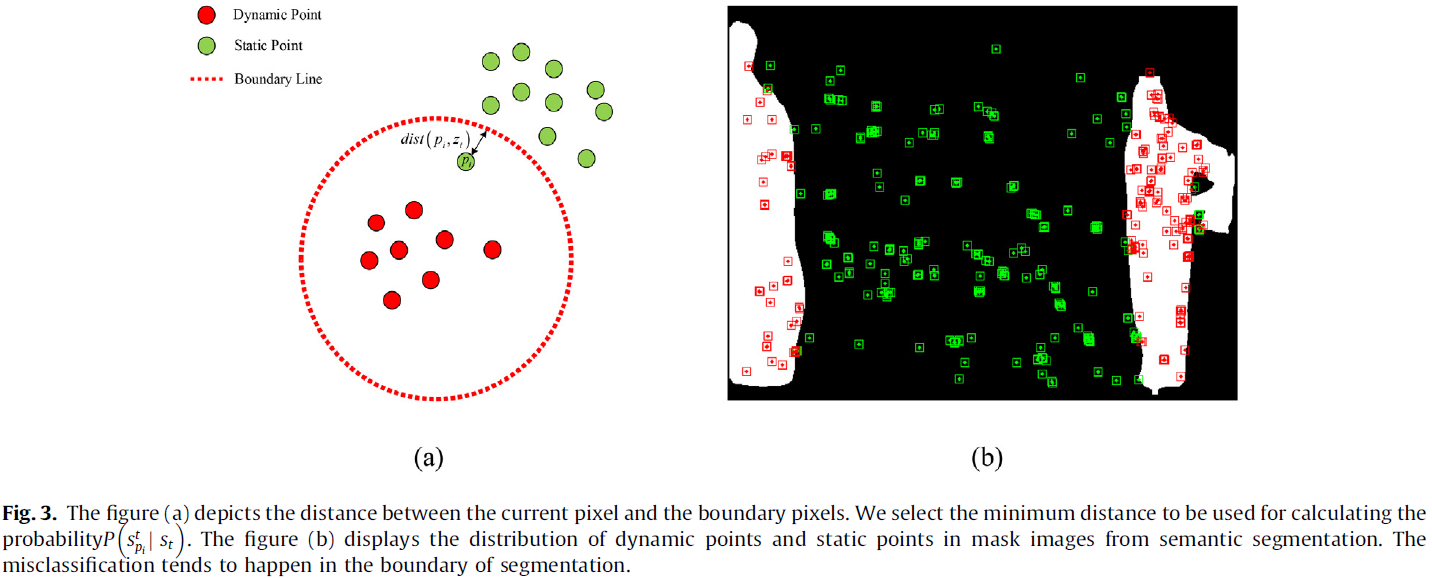
具体地,取 spit 为关键点 pi 在时间 t 由语义分割得到的标签,定义为:
spit={1,0,if pi is determined as dynamicotherwise(1)
取 st 为关键点标签的集合(n 为关键点的数量):
st={sp1t,sp2t,...,spnt}(2)
t 时刻的边界像素为:
zt={b1t,b2t,...,bmt}(3)
bmt 表示动态物体分割区域的边界点,m 为边界点的数量。所有的边界点都包含在 zt 中。
关键点 pi 和分割区域的边界的距离定义为:
dist(pi,zt)=bjt∈ztmin∥pi−bjt∥2(4)
二项逻辑回归模型用于估计 pi 的动态概率(α(=0.1) 为平滑因子):
P(spit∣st)=exp(−α⋅dist(pi,zt))+11(5)
动态概率是指被分割掩码中的关键点与边界边缘的距离越近,误分类的概率越高。因此,如果掩码中的 pi 具有异常的低概率(<0.75),则它更有可能是一个静态关键点,尽管它位于掩码内。
2.3 Epipolar Geometry Constraint
由于 Mask R-CNN 是使用 COCO 数据集训练的,只能确定大约 80 个类别的对象,因此仍然存在一些无法通过语义分割检测到的移动对象。为了解决这一问题,在两个连续帧之间使用对极几何约束来进一步确定动态关键点:
- 运动物体的匹配关键点不满足对极几何约束,因为这些关键点并不严格地位于相应的极线上。因此,计算匹配关键点到极线的距离,如果距离大于某一阈值,则将匹配点定义为异常值。
Fig.4 表示前一帧 I1 和当前帧 I2 之间的对极几何约束:
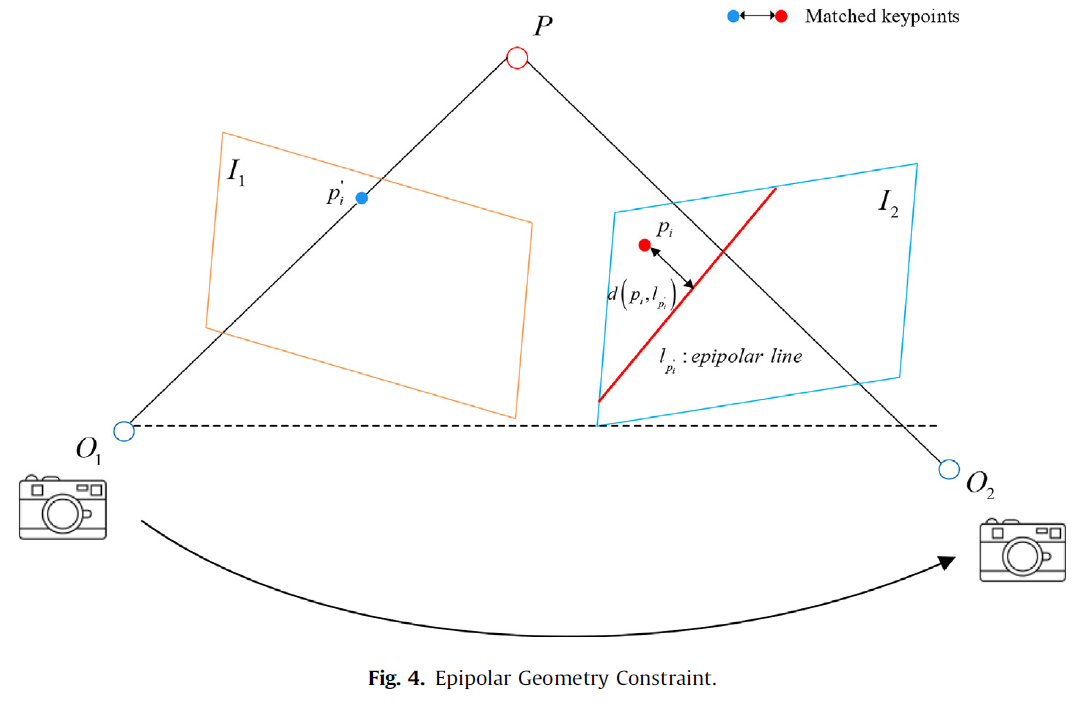
设 pi′ 和 pi 分别表示前一帧和当前帧中匹配的关键点对(x,y 为匹配关键点的像素坐标):
pi′=[xpi′,ypi′,1],pi=[xpi,ypi,1](6)
极线 lpi 定义为(X,Y,Z 表示极线向量,F 为基础矩阵):
lpi=⎣⎡Xpi′Ypi′Zpi′⎦⎤=F(pi′)T=F⎣⎡xpi′ypi′1⎦⎤(7)
从匹配点 pi 到极线 lpi 的距离定义为:
d(pi,lpi)=∥Xpi′∥2+∥Ypi′∥2∣piFpi′∣(8)
拒绝动态 outliers 的步骤如下:
- 通过计算当前帧的光流金字塔得到匹配关键点。如果匹配点太接近图像的边缘,或者以匹配点为中心的 3×3 图像块的像素差太大,则删除匹配的关键点对。
- 使用 RANSAC 算法求得基础矩阵,再计算匹配点到极线的距离,当距离大于一定阈值时(>0.75),将匹配点视为 outliers。
- 通过几何方法确定了动态关键点。
算法如下:

取 cpit 为 t 时刻几何方法确定的关键点 pi 的标签,S 为动态点集:
cpit={1,0,if pi∈Sotherwise(9)
同样,取 ct 为 t 时刻的关键点标签集,n 为关键点数:
ct={cp1t,cp2t,...,cpnt}(10)
由于运动物体的存在,图像中的每个关键点没有严格约束在其对应的极线上:
因此, 假定匹配关键点到对应极线的距离满足高斯分布,使用正态分布概率密度函数来计算关键点的动态概率:
P(cpit∣ct)=2πδ1exp(−2δ2d(pi,lpi)2)(11)
δ(=1) 为标准差,且分布的期望值为 0。
2.4 Iteratively Moving Probability Update
传统的几何或语义 VIO 只是在单一帧中消除动态点。但是,跟踪动态对象可以大大提高定位性能。本文的方法考虑的视觉里程计的动态离群值拒绝问题远不止一帧:
- 本文提出了一种动态概率传播算法,该算法结合了几何模型和基于深度学习的算法来去除图像中的动态目标。基于贝叶斯定理,利用过去和当前的信息来评估和消除动态关键点。
定义匹配点 pi 在时刻 t 的真实状态为 Dt(pi):
- 如果 pi 在动态物体的区域内,则定义该点为动态点,即有 Dt(pi)=1;否则 Dt(pi)=0。
由几何模型得到的动态概率 P(Dt(pi)∣cpit) 和由语义分割得到的动态概率 P(Dt(pi)∣spit) 可以联合为:
P(Dt(pi)=1∣cpit,spit)=ωP(Dt(pi)=1∣cpit)+(1−ω)P(Dt(pi)=1∣spit)(12)
P(Dt(pi)=0∣cpit,spit)=ωP(Dt(pi)=0∣cpit)+(1−ω)P(Dt(pi)=0∣spit)(13)
ω 定义为:
ω=Nc+NsNc(14)
Nc 为当前帧被几何模型所拒绝的 outliers 的数量,Ns 为当前帧被语义分割拒绝的 outliers 的数量(可以将 outliers 理解为相应方法产生的动态关键点)。
假设动态概率的传播具有马尔可夫性,基于贝叶斯理论,关键点的动态概率传播模型可以定义为:
P(Dt(pi)∣cpit,spit)=ηP(cpit,spit∣Dt(pi))⋅∫P(Dt(pi)∣Dt−1(pi))⋅P(Dt−1(pi))dDt−1(pi)(15)
关键点在前一帧中的动态概率被视为先验概率,η 为规范化影响因子。观测概率 P(cpit,spit∣Dt(pi)) 表述为:
P(cpit,spit∣Dt(pi))=P(Dt(pi)=1)⋅P(cpit,spit∣Dt(pi)=1)+P(Dt(pi)=0)⋅P(cpit,spit∣Dt(pi)=0)(16)
其中有:
P(cpit,spit∣Dt(pi)=0)=P(Dt(pi)=0)P(cpit,spit,Dt(pi)=0)=P(Dt(pi)=0)P(cpit,spit)P(Dt(pi)=0∣cpit,spit)(17)
P(cpit,spit∣Dt(pi)=1)=P(Dt(pi)=1)P(cpit,spit,Dt(pi)=1)=P(Dt(pi)=1)P(cpit,spit)P(Dt(pi)=1∣cpit,spit)(18)
整个算法如下,由算法 2 所确定的 U 里的每一个关键点都认为是 outliers,需要从当前帧中移除:

根据 (5) 和 (11),可以获得语义分割动态概率 P(spit∣st) 和几何模型动态概率 P(cpit∣ct),从而使用 (12-13) 和 (16-18) 可以求得观测概率 P(cpit,spit∣Dt(pi))。再由 (15) 可以更新动态概率 P(Dt(pi)∣cpit,spit)。
- 文中没有明确说明,按照各符号的含义及表达式,认为:
ηP(cpit,spit)P(Dt(pi)=1∣cpit)P(Dt(pi)=0∣cpit)P(Dt(pi)=1∣spit)P(Dt(pi)=0∣spit)P(Dt−1(pi))=1/P(cpit,spit)=P(cpit∣ct)⋅P(spit∣st)=P(cpit∣ct)=1−P(cpit∣ct)=P(spit∣st)=1−P(spit∣st)=P(Dt−1(pi)∣cpit−1,spit−1)(批注)
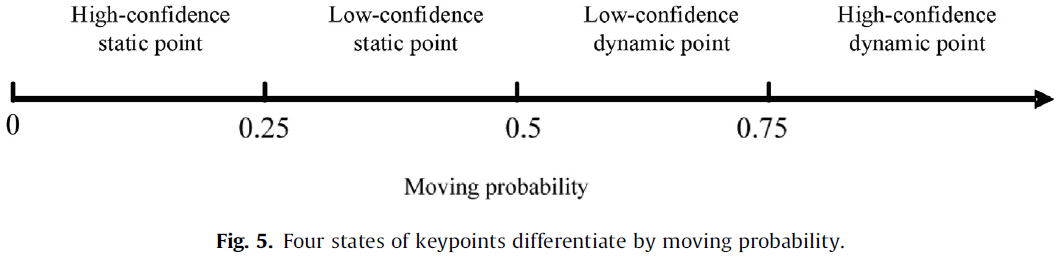
如 Fig.5,根据动态概率将关键点分为四个状态。当动态概率满足 P(Dt(pi)∣cpit,spit)>0.5 时认为关键点为动态 outlier。
2.5 Background Inpainting
移除动态物体后,根据之前的静态观察,重绘被动态物体遮挡的背景。合成一个没有动态内容的真实图像,这有助于回环检测和建图,使 SLAM 满足在静态环境假设下工作。
由于之前帧和当前帧是已知的,从所有之前的关键帧(实验中取当前帧的前 20 帧)投影到当前帧的 RGB 图和深度图的动态区域。合成帧中可能有一些区域是空白的,这是由于这些区域可能目前为止未出现,或者在之前被过滤掉了。
Fig.6 为 TUM 数据集的合成图像:

3 Experimental Results and Analysis
3.1 Experimental Setup
- 实验数据集:TUM RGB-D
- 低动态数据序列:sitting static,sitting halfsphere
- 高动态数据序列:walking
- 设备:Intel i5-8265U 3.7GHz,16GB RAM,NVIDIA GeForce MX150
- baseline:ORB-SLAM2
3.2 Experimental Results
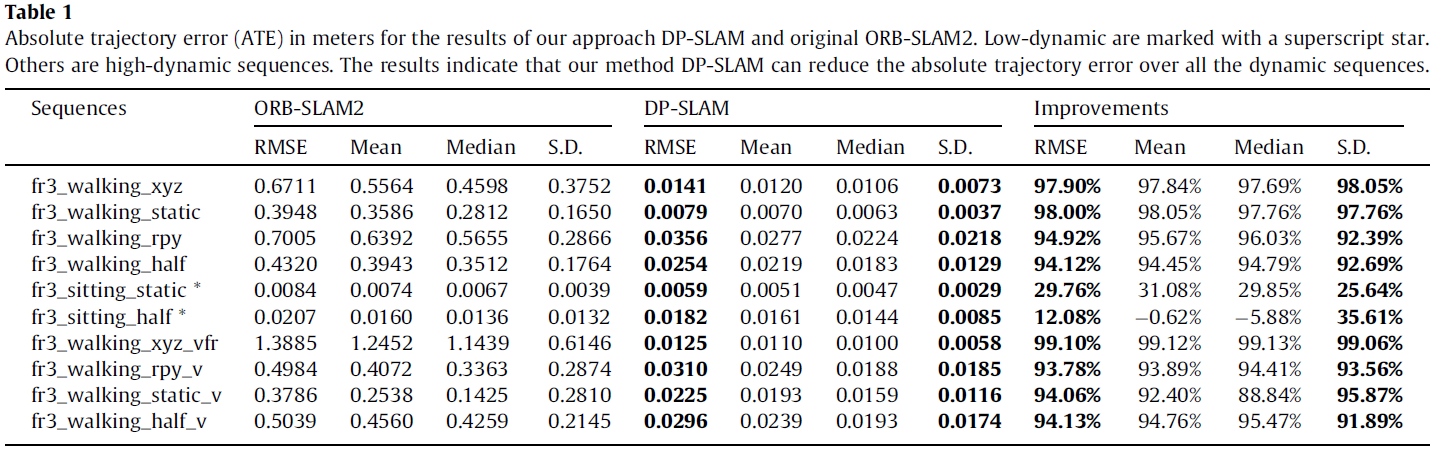
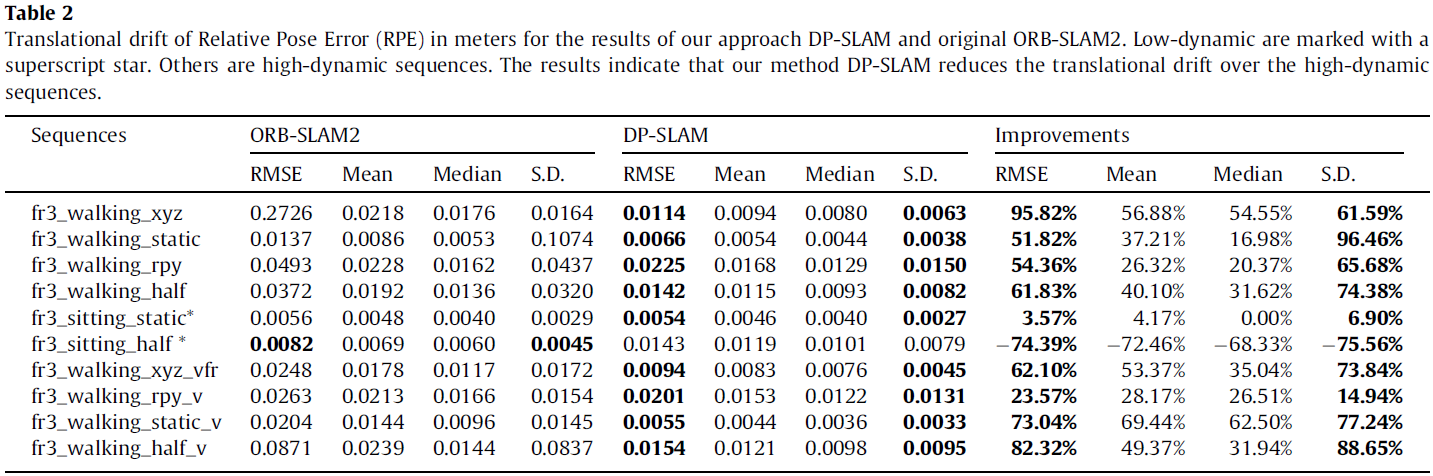
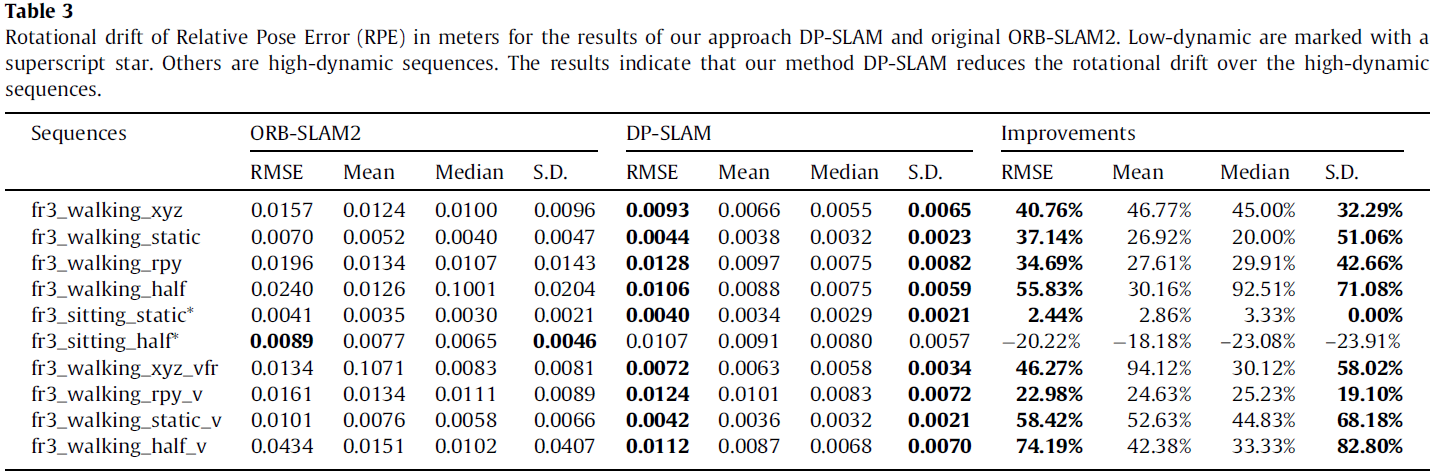
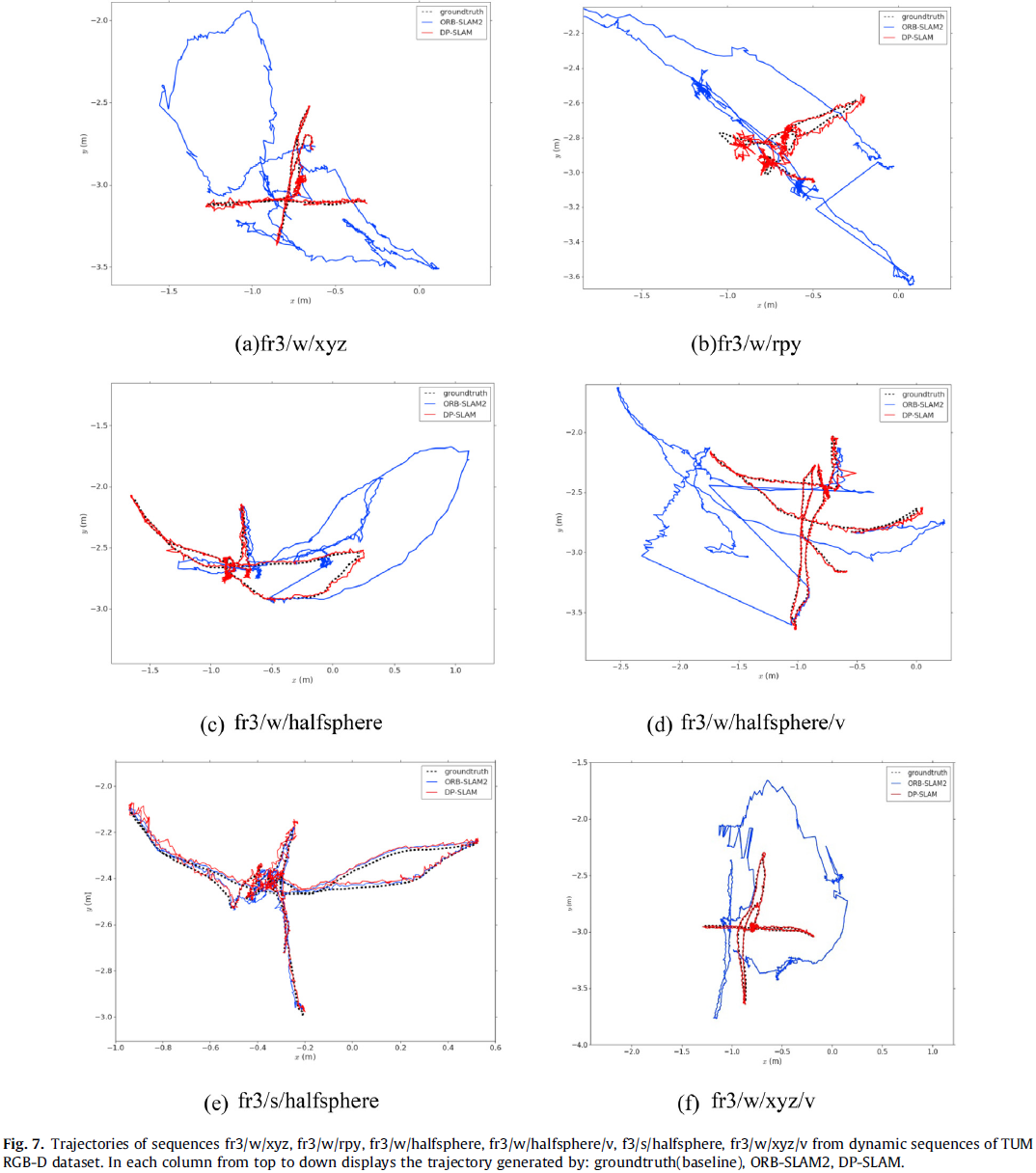
对于 improvements 的定义:
Γ=(1−αβ)×100%(19)
α 为 baseline 的结果,β 为 DP-SLAM 的结果。
语义分割和动态关键点提取效果(数据集和真实世界):


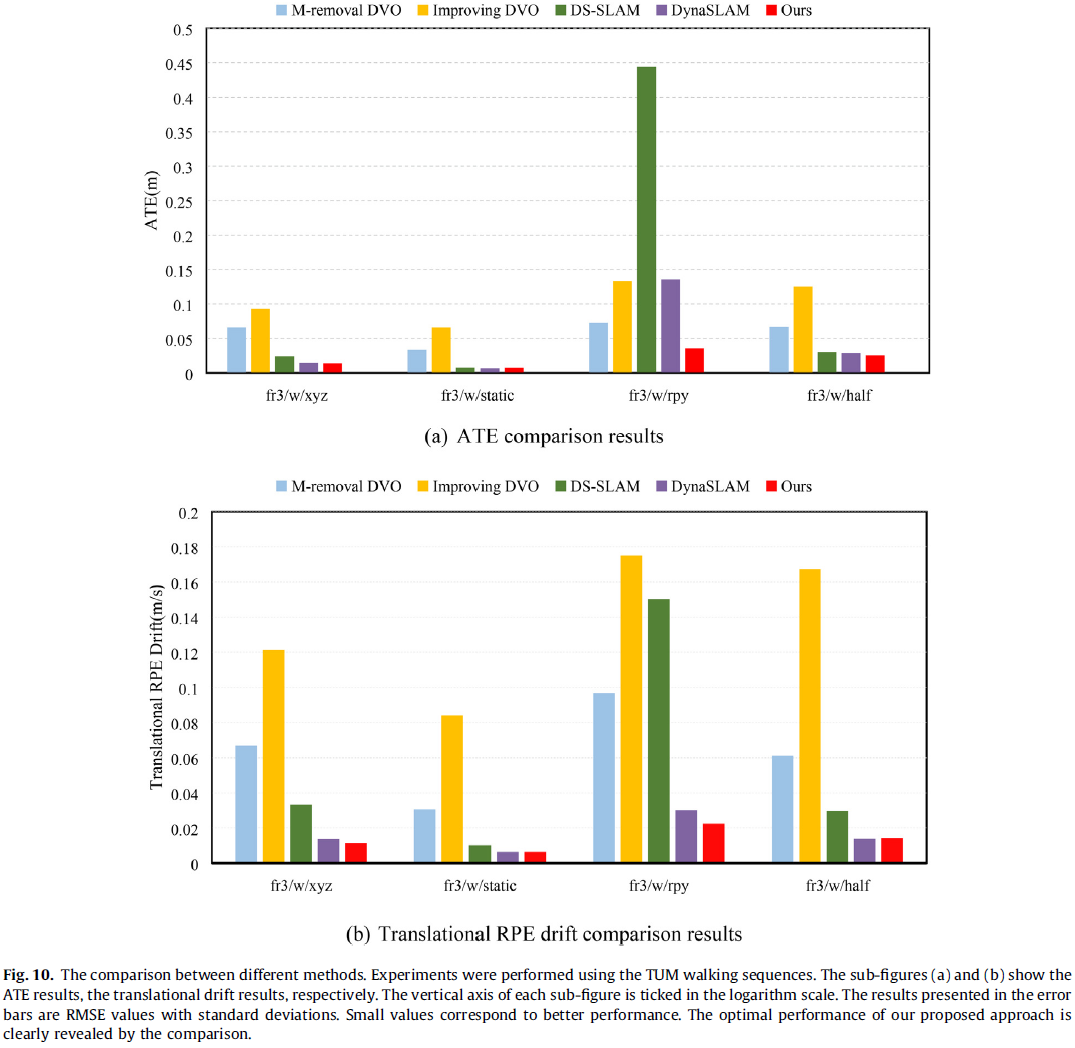
3.3 Method Comparison
参考
- [1] K. He, G. Gkioxari, P. Dollar, R. Girshick, Mask R-CNN, IEEE Trans. Pattern Anal. Mach. Intell. 42 (2) (2020) 386–397.














