关于论文 DRG-SLAM: A Semantic RGB-D SLAM using Geometric Features for Indoor Dynamic Scene (IROS, 2022) 的阅读总结。
DRG-SLAM
标题:DRG-SLAM: A Semantic RGB-D SLAM using Geometric Features for Indoor Dynamic Scene
作者:Yanan Wang, Kun Xu, Yaobin Tian, Xilun Ding
会议:IROS, 2022
源码:未开源
在 SLAM 中使用深度学习来识别动态物体,然而由于仅点特征被使用,在结构不清的室内环境中 SLAM 的鲁棒性将会受限。当动态物体占据大部分图像时,移除这些区域的点将会使剩余用于定位的特征点减少。
本文提出动态 RGB-D 几何 SLAM —— DRG-SLAM,在点特征的基础上加入线特征和面特征,用于识别环境中的几何结构。利用极线约束和深度学习对动态对象进行特征检测和剔除。然后,利用多视图约束对未被语义分割的动态对象进行特征细化;最后构建点、线、面组成的静态地图。
文章贡献:
提出了一种结合语义分割和对极约束的动态特征剔除方法,先剔除识别到的动态对象上的特征,再通过多视图约束剔除未识别到的动态对象上的动态特征。
添加线、平面特征作为,提高在结构不清晰和动态环境下 SLAM 的鲁棒性,并构建包含这些几何特征的静态地图。
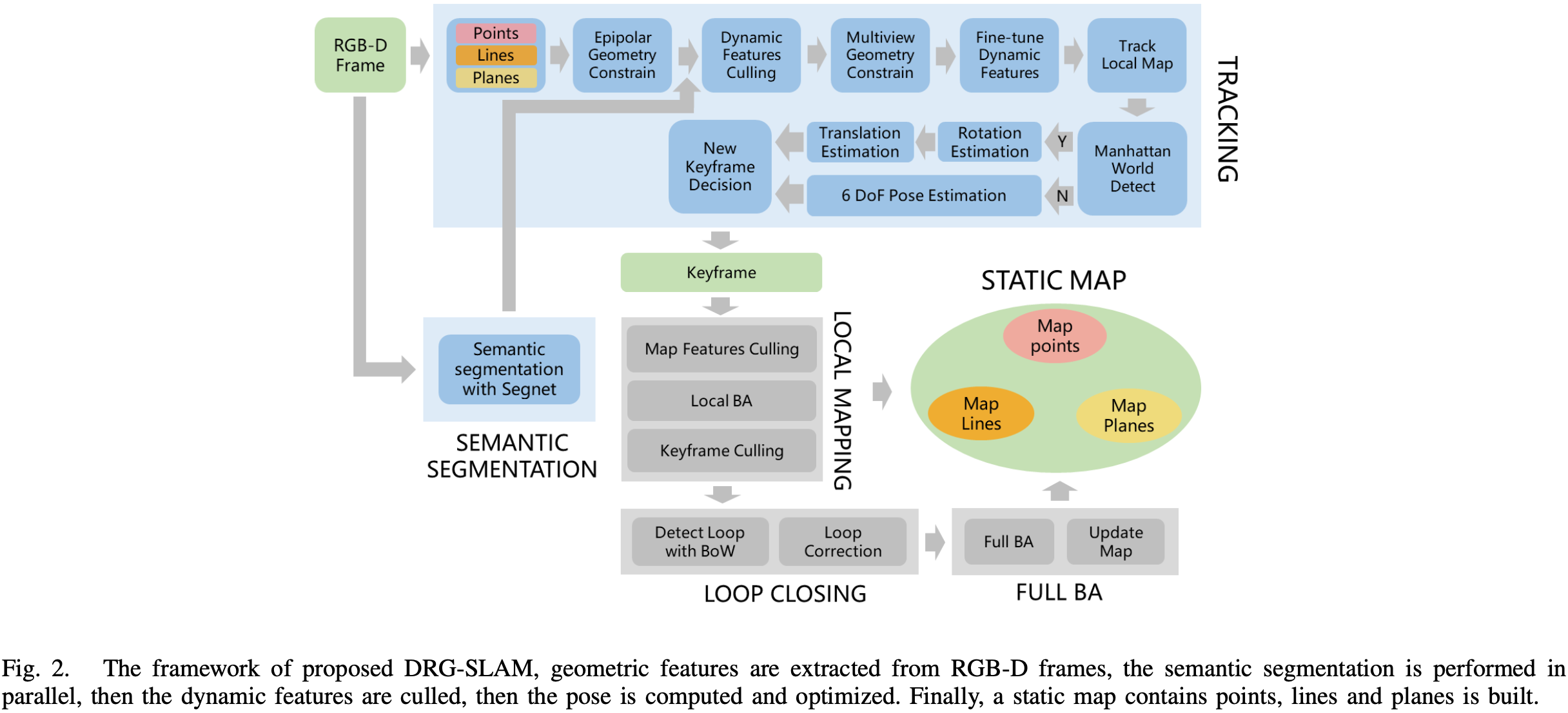
系统总体框架框如图-2,包含语义分割、跟踪、局部建图、回环检测、全束平差和建图。
首先,在新 RGB 图和深度图到达后,跟踪线程提取点、线和平面特征,并通过对极约束识别出潜在的几何特征动态点,包括特征点、线端点、平面上的点;
同时,语义分割线程使用深度学习网络对输入图像进行语义分割并将结果传递给跟踪线程;
然后,跟踪线程根据语义信息,检测对极几何初始筛选得到的潜在动态点是否落在动态物体上,如果落在这些物体上的潜在动态点达到一定数量,则认为该物体是动态的,并去除其上的所有特征;
然而,语义分割只能检测特定数量的训练对象。因此,后续对多视图进行约束以进一步去除动态特征,之后对剩余的静态特征进行跟踪、构建地图等操作。
点是视觉 SLAM 中最常用的特征,但在室内环境中存在墙壁、走廊等无纹理的场景,且存在动态物体的遮挡,因此很难提取足够数量的点特征,在高动态场景中甚至会丢失跟踪,因此添加线、面特征以提高鲁棒性。
**(1)点特征:**使用 ORB 作为点特征。记 3D 空间的点为 P w = ( X , Y , Z ) T \mathbf{P}_w = (X, Y, Z)^T P w = ( X , Y , Z ) T p c = ( u , v ) T \mathbf{p}_c = (u, v)^T p c = ( u , v ) T
**(2)线特征:**LSD 法[1] 和基于外表的 LBD 描述子[2] 用于提取和匹配线特征。将线特征用两个端点表示,3D 空间中的线特征为 L = ( S L , E L ) \mathbf{L} = (\mathbf{S}_L, \mathbf{E}_L) L = ( S L , E L ) l = ( s l , e l ) \mathbf{l} = (\mathbf{s}_l, \mathbf{e}_l) l = ( s l , e l )
**(3)面特征:**使用 Agglomerative Hierarchical Clustering 法[3] 提取面特征,其能够从有序点云中提取平面特征。为了便于平面特征的表示,使用 Hesse 范式来描述空间平面:
n 0 ⋅ r − d = 0 (1) \mathbf{n}_0 \cdot \mathbf{r} - d = 0
\tag{1}
n 0 ⋅ r − d = 0 ( 1 )
n 0 = ( n x , n y , n z ) T \mathbf{n}_0 = (n_x, n_y, n_z)^T n 0 = ( n x , n y , n z ) T r \mathbf{r} r d d d
2.2 中的特征提取是对所有对象进行。在动态场景下,当提取的特征在运动物体上时,定位精度可能会降低。为了解决这个问题,应该删除动态对象上的特性。
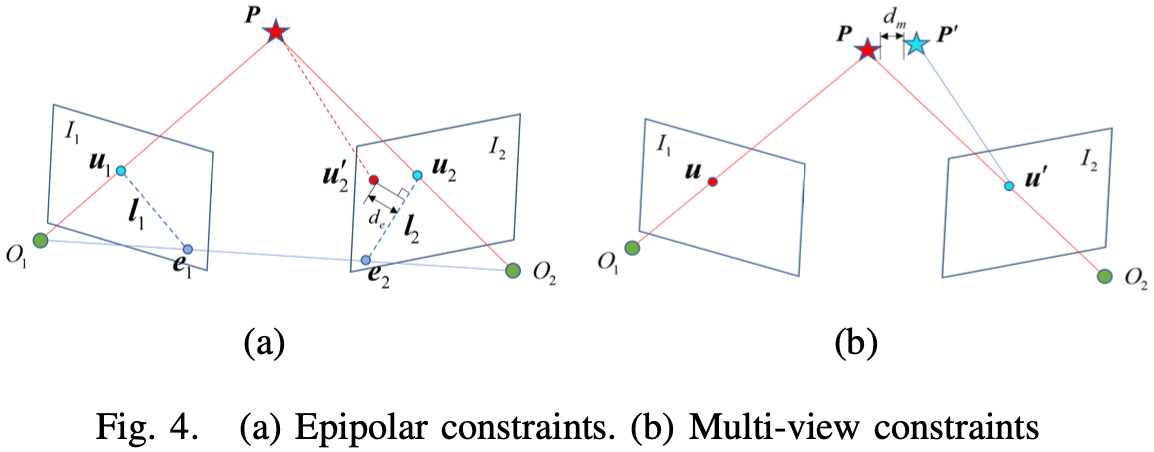
**(1)对极约束:**检测潜在的动态点,包括特征点、线的端点和平面上的点。对于两帧 I 1 , I 2 I_1, I_2 I 1 , I 2 O 1 , O 2 O_1, O_2 O 1 , O 2 u 1 \mathbf{u}_1 u 1 I 1 I_1 I 1 u 2 \mathbf{u}_2 u 2
若特征匹配正确,O 1 u 1 O_1 \mathbf{u}_1 O 1 u 1 O 2 u 2 O_2 \mathbf{u}_2 O 2 u 2 P \mathbf{P} P
u 2 T K − T t ∧ K − 1 u 1 = u 2 T F u 1 = 0 (2) \mathbf{u}_2^T \mathbf{K}^{-T} \mathbf{t}^{\wedge} \mathbf{K}^{-1} \mathbf{u}_1 = \mathbf{u}_2^T \mathbf{F} \mathbf{u}_1 = 0
\tag{2}
u 2 T K − T t ∧ K − 1 u 1 = u 2 T F u 1 = 0 ( 2 )
l 2 = F u 2 = ( a , b , c ) T (3) \mathbf{l}_2 = \mathbf{Fu}_2 = (a, b, c)^T
\tag{3}
l 2 = F u 2 = ( a , b , c ) T ( 3 )
F \mathbf{F} F u 2 ′ \mathbf{u}_2^{\prime} u 2 ′ d e d_e d e u 2 ′ \mathbf{u}_2^{\prime} u 2 ′
d e = ∣ u 2 T F u 1 ∣ a 2 + b 2 (4) d_e = \frac{| \mathbf{u}_2^T \mathbf{F} \mathbf{u}_1 |}{\sqrt{a^2 + b^2}}
\tag{4}
d e = a 2 + b 2 ∣ u 2 T F u 1 ∣ ( 4 )
若 d e d_e d e d e t h d_{eth} d e t h u 2 ′ \mathbf{u}_2^{\prime} u 2 ′
**(2)语义分割:**在几何特征提取时,并行地运行语义分割线程。SegNet 基于 Caffe 框架对输入的图像帧进行语义分割。该模型在 Pascal VOC 数据集上进行训练,能够识别包括人、椅子、显示器等 20 种物体。
**(3)动态特征提取:**RGB 帧未经过动态特征剔除的所有特征如图-3 (a) 所示,大量的特征落在人身上。动态物体的语义掩码中的所有特征都应该被移除。
深度学习方法只能识别特定种类的物体,无法检测到一些训练数据集中未预定义的动态物体,如人手握的气球(图-3 (b)),需要进一步细化以剔除这些动态对象上的特征。采用多视角约束(图-4 (b))进一步去除这些动态特征。图-3 © 展示了全动态特征剔除的结果。
定义第一个相机坐标系为世界坐标系 w w w T w n , T w i ∈ S E ( 3 ) \mathbf{T}_{wn}, \mathbf{T}_{wi} \in SE(3) T w n , T w i ∈ S E ( 3 ) n n n i i i u \mathbf{u} u n ( = 3 ) n (=3) n ( = 3 ) z z z P \mathbf{P} P π \pi π
P = T w n π − 1 ( u , z ) (5) \mathbf{P} = \mathbf{T}_{wn} \pi^{-1} (\mathbf{u}, z)
\tag{5}
P = T w n π − 1 ( u , z ) ( 5 )
将 P \mathbf{P} P i i i
u ′ = π ( T w i − 1 P ) (6) \mathbf{u}^{\prime} = \pi (\mathbf{T}_{wi}^{-1} \mathbf{P})
\tag{6}
u ′ = π ( T w i − 1 P ) ( 6 )
将 u ′ \mathbf{u}^{\prime} u ′ z ′ z^{\prime} z ′ P ′ \mathbf{P}^{\prime} P ′
P ′ = T w i π − 1 ( u ′ , z ′ ) (7) \mathbf{P}^{\prime} = \mathbf{T}_{wi} \pi^{-1} (\mathbf{u}^{\prime}, z^{\prime})
\tag{7}
P ′ = T w i π − 1 ( u ′ , z ′ ) ( 7 )
如果特征点是静态的,点 P \mathbf{P} P P ′ \mathbf{P}^{\prime} P ′ d m t h d_{mth} d m t h
在跟踪阶段,检查环境是否满足 Manhattan World 假设,即环境中是否存在三个相互垂直的平面。实际上,只需要检测两个相互垂直的平面法向量,通过它们的叉乘即可得到另一个平面的法向量。如果检测到 Manhattan 世界,则分别估计相机位姿的旋转和平移以减少漂移,否则同时估计旋转和平移。
**(1)曼哈顿世界位姿估计:**如果环境满足曼哈顿世界假设,则先估计旋转。设 R w m , R m i ∈ S O ( 3 ) \mathbf{R}_{wm}, \mathbf{R}_{mi} \in SO(3) R w m , R m i ∈ S O ( 3 ) m m m i i i R w i = R w m R m i \mathbf{R}_{wi} = \mathbf{R}_{wm} \mathbf{R}_{mi} R w i = R w m R m i R w m , R m i \mathbf{R}_{wm}, \mathbf{R}_{mi} R w m , R m i R w i \mathbf{R}_{wi} R w i t w i \mathbf{t}_{wi} t w i
地图点记作 P w j = ( x j , y j , z j ) T \mathbf{P}_{wj} = (x_j, y_j, z_j)^T P w j = ( x j , y j , z j ) T i i i u i j = ( u i j , v i j ) T \mathbf{u}_{ij} = (u_{ij}, v_{ij})^T u i j = ( u i j , v i j ) T
r p o i n t i j = u i j − π ( R w i T P w j − R w i T t w i ) = u i j − π ( T w i − 1 P w j ) (8) \mathbf{r}_{\mathrm{point}_{ij}} = \mathbf{u}_{ij} - \pi(\mathbf{R}_{wi}^T \mathbf{P}_{wj} - \mathbf{R}_{wi}^T \mathbf{t}_{wi}) = \mathbf{u}_{ij} - \pi(\mathbf{T}_{wi}^{-1} \mathbf{P}_{wj})
\tag{8}
r p o i n t i j = u i j − π ( R w i T P w j − R w i T t w i ) = u i j − π ( T w i − 1 P w j ) ( 8 )
对于线特征,点到线的距离作为误差函数。记第 k k k S w k = ( x s k , y s k , z s k ) \mathbf{S}_{wk} = (x_{sk}, y_{sk}, z_{sk}) S w k = ( x s k , y s k , z s k ) E w k = ( x e k , y e k , z e k ) \mathbf{E}_{wk} = (x_{ek}, y_{ek}, z_{ek}) E w k = ( x e k , y e k , z e k ) i i i
l i k : a k x + b k y + c k = 0 (9) \mathbf{l}_{ik}: a_k x + b_k y + c_k = 0
\tag{9}
l i k : a k x + b k y + c k = 0 ( 9 )
取其端点的齐次坐标 s i k = ( u s k , v s k , 1 ) , e i k = ( u e k , v e k , 1 ) \mathbf{s}_{ik} = (u_{sk}, v_{sk}, 1), \mathbf{e}_{ik} = (u_{ek}, v_{ek}, 1) s i k = ( u s k , v s k , 1 ) , e i k = ( u e k , v e k , 1 )
l i k = ( a k , b k , c k ) T = s i k × e i k (10) \mathbf{l}_{ik} = (a_k, b_k, c_k)^T = \mathbf{s}_{ik} \times \mathbf{e}_{ik}
\tag{10}
l i k = ( a k , b k , c k ) T = s i k × e i k ( 1 0 )
第 k k k m w k = ( S w k + E w k ) / 2 \mathbf{m}_{wk} = (\mathbf{S}_{wk} + \mathbf{E}_{wk}) / 2 m w k = ( S w k + E w k ) / 2
r l i n e i k = l i k T π ( R w i T m w k − R w i T t w i ) a k 2 + b k 2 (11) \mathbf{r}_{\mathrm{line}_{ik}} = \frac{\mathbf{l}_{ik}^T \pi(\mathbf{R}_{wi}^T \mathbf{m}_{wk} - \mathbf{R}_{wi}^T \mathbf{t}_{wi})}{\sqrt{a_k^2 + b_k^2}}
\tag{11}
r l i n e i k = a k 2 + b k 2 l i k T π ( R w i T m w k − R w i T t w i ) ( 1 1 )
对于面特征,法向量间的角度差和面到原点的距离差用于误差函数。设面特征表示为 π = ( n 0 , d ) T \pi = (\mathbf{n}_0, d)^T π = ( n 0 , d ) T n 0 \mathbf{n}_0 n 0 n 0 s = ( r , θ , φ ) T \mathbf{n}_{0s} = (r, \theta, \varphi)^T n 0 s = ( r , θ , φ ) T r r r θ \theta θ φ \varphi φ
{ r = n 0 x 2 + n 0 y 2 + n 0 z 2 = 1 θ = arccos ( n 0 z / r ) = arccos ( n 0 z ) φ = arctan ( n 0 y / n 0 x ) (12) \begin{cases}
r = \sqrt{n_{0x}^2 + n_{0y}^2 + n_{0z}^2} = 1 \\
\theta = \arccos (n_{0z} / r) = \arccos (n_{0z}) \\
\varphi = \arctan (n_{0y} / n_{0x})
\end{cases}
\tag{12}
⎩ ⎪ ⎪ ⎨ ⎪ ⎪ ⎧ r = n 0 x 2 + n 0 y 2 + n 0 z 2 = 1 θ = arccos ( n 0 z / r ) = arccos ( n 0 z ) φ = arctan ( n 0 y / n 0 x ) ( 1 2 )
由于 r r r s ( π ) = ( θ , φ , d ) T , θ , φ ∈ ( − π , π ] s(\pi) = (\theta, \varphi, d)^T, \theta, \varphi \in (-\pi, \pi] s ( π ) = ( θ , φ , d ) T , θ , φ ∈ ( − π , π ] l l l π w l \pi_{wl} π w l i i i π i l \pi_{il} π i l
r p l a n e i l = s ( π i l ) − s ( T w i − 1 π w l ) (13) \mathbf{r}_{\mathrm{plane}_{il}} = s(\pi_{il}) - s(\mathbf{T}_{wi}^{-1} \pi_{wl})
\tag{13}
r p l a n e i l = s ( π i l ) − s ( T w i − 1 π w l ) ( 1 3 )
在结构化环境中,存在平行平面和垂直平面,将这些约束加入到平面特征的误差函数中。平行平面和垂直平面的误差为:
r p a r − p l a n e i l = s ( n i l ) − s ( R w i − 1 n w l ) (14) \mathbf{r}_{\mathrm{par-plane}_{il}} = s(\mathbf{n}_{il}) - s(\mathbf{R}_{wi}^{-1} \mathbf{n}_{wl})
\tag{14}
r p a r − p l a n e i l = s ( n i l ) − s ( R w i − 1 n w l ) ( 1 4 )
r p e r − p l a n e i l = s ( R ⊥ n i l ) − s ( R w i − 1 n w l ) (15) \mathbf{r}_{\mathrm{per-plane}_{il}} = s(\mathbf{R}_{\perp} \mathbf{n}_{il}) - s(\mathbf{R}_{wi}^{-1} \mathbf{n}_{wl})
\tag{15}
r p e r − p l a n e i l = s ( R ⊥ n i l ) − s ( R w i − 1 n w l ) ( 1 5 )
R ⊥ \mathbf{R}_{\perp} R ⊥
r π i l = r p l a n e i l + r p a r − p l a n e i l + r p e r − p l a n e i l (16) \mathbf{r}_{\pi_{il}} = \mathbf{r}_{\mathrm{plane}_{il}} + \mathbf{r}_{\mathrm{par-plane}_{il}} + \mathbf{r}_{\mathrm{per-plane}_{il}}
\tag{16}
r π i l = r p l a n e i l + r p a r − p l a n e i l + r p e r − p l a n e i l ( 1 6 )
由于 R w i \mathbf{R}_{wi} R w i t w i \mathbf{t}_{wi} t w i
t w i ∗ = arg min t w i ∑ j ∈ P ρ h ( r p o i n t i j T Σ p o i n t i j − 1 r p o i n t i j ) + ∑ k ∈ L ρ h ( r l i n e i k T Σ l i n e i k − 1 r l i n e i k ) + ∑ l ∈ Π ρ h ( r π i l T Σ π i l − 1 r π i l ) (17) \begin{aligned}
\mathbf{t}_{wi}^{*} &= \arg \min_{\mathbf{t}_{wi}} \sum_{j \in \mathcal{P}} \rho_h \left( \mathbf{r}_{\mathrm{point}_{ij}}^T \Sigma_{\mathrm{point}_{ij}}^{-1} \mathbf{r}_{\mathrm{point}_{ij}} \right) \\
&+ \sum_{k \in \mathcal{L}} \rho_h \left( \mathbf{r}_{\mathrm{line}_{ik}}^T \Sigma_{\mathrm{line}_{ik}}^{-1} \mathbf{r}_{\mathrm{line}_{ik}} \right) \\
&+ \sum_{l \in \Pi} \rho_h \left( \mathbf{r}_{\pi_{il}}^T \Sigma_{\pi_{il}}^{-1} \mathbf{r}_{\pi_{il}} \right)
\end{aligned}
\tag{17}
t w i ∗ = arg t w i min j ∈ P ∑ ρ h ( r p o i n t i j T Σ p o i n t i j − 1 r p o i n t i j ) + k ∈ L ∑ ρ h ( r l i n e i k T Σ l i n e i k − 1 r l i n e i k ) + l ∈ Π ∑ ρ h ( r π i l T Σ π i l − 1 r π i l ) ( 1 7 )
ρ h \rho_h ρ h
**(2)非曼哈顿世界位姿估计:**如果环境中没有检测到曼哈顿世界帧,则同时估计旋转和平移,且每个几何特征的误差函数与曼哈顿世界的误差函数相同,而非曼哈顿世界的优化为:
R w i ∗ , t w i ∗ = arg min R w i , t w i ∑ j ∈ P ρ h ( r p o i n t i j T Σ p o i n t i j − 1 r p o i n t i j ) + ∑ k ∈ L ρ h ( r l i n e i k T Σ l i n e i k − 1 r l i n e i k ) + ∑ l ∈ Π ρ h ( r π i l T Σ π i l − 1 r π i l ) (18) \begin{aligned}
\mathbf{R}_{wi}^{*}, \mathbf{t}_{wi}^{*} &= \arg \min_{\mathbf{R}_{wi}, \mathbf{t}_{wi}} \sum_{j \in \mathcal{P}} \rho_h \left( \mathbf{r}_{\mathrm{point}_{ij}}^T \Sigma_{\mathrm{point}_{ij}}^{-1} \mathbf{r}_{\mathrm{point}_{ij}} \right) \\
&+ \sum_{k \in \mathcal{L}} \rho_h \left( \mathbf{r}_{\mathrm{line}_{ik}}^T \Sigma_{\mathrm{line}_{ik}}^{-1} \mathbf{r}_{\mathrm{line}_{ik}} \right) \\
&+ \sum_{l \in \Pi} \rho_h \left( \mathbf{r}_{\pi_{il}}^T \Sigma_{\pi_{il}}^{-1} \mathbf{r}_{\pi_{il}} \right)
\end{aligned}
\tag{18}
R w i ∗ , t w i ∗ = arg R w i , t w i min j ∈ P ∑ ρ h ( r p o i n t i j T Σ p o i n t i j − 1 r p o i n t i j ) + k ∈ L ∑ ρ h ( r l i n e i k T Σ l i n e i k − 1 r l i n e i k ) + l ∈ Π ∑ ρ h ( r π i l T Σ π i l − 1 r π i l ) ( 1 8 )
**(3)静态建图:**地图构建模块构建包含静态点特征、线特征和面特征的地图。每当新的关键帧出现时,提取关键帧的几何特征,进行动态特征剔除,然后根据深度图提供的深度信息将静态特征添加到图中。
点特征和线特征使用类似 ORB-SLAM2 的方法,平面特征使用类似 Planar-SLAM 的方法,即检测当前面特征与地图中的面特征是否有足够的匹配,如果有足够的匹配,则更新地图中对应平面上的点,如果没有找到匹配平面,则将该平面添加到地图中。
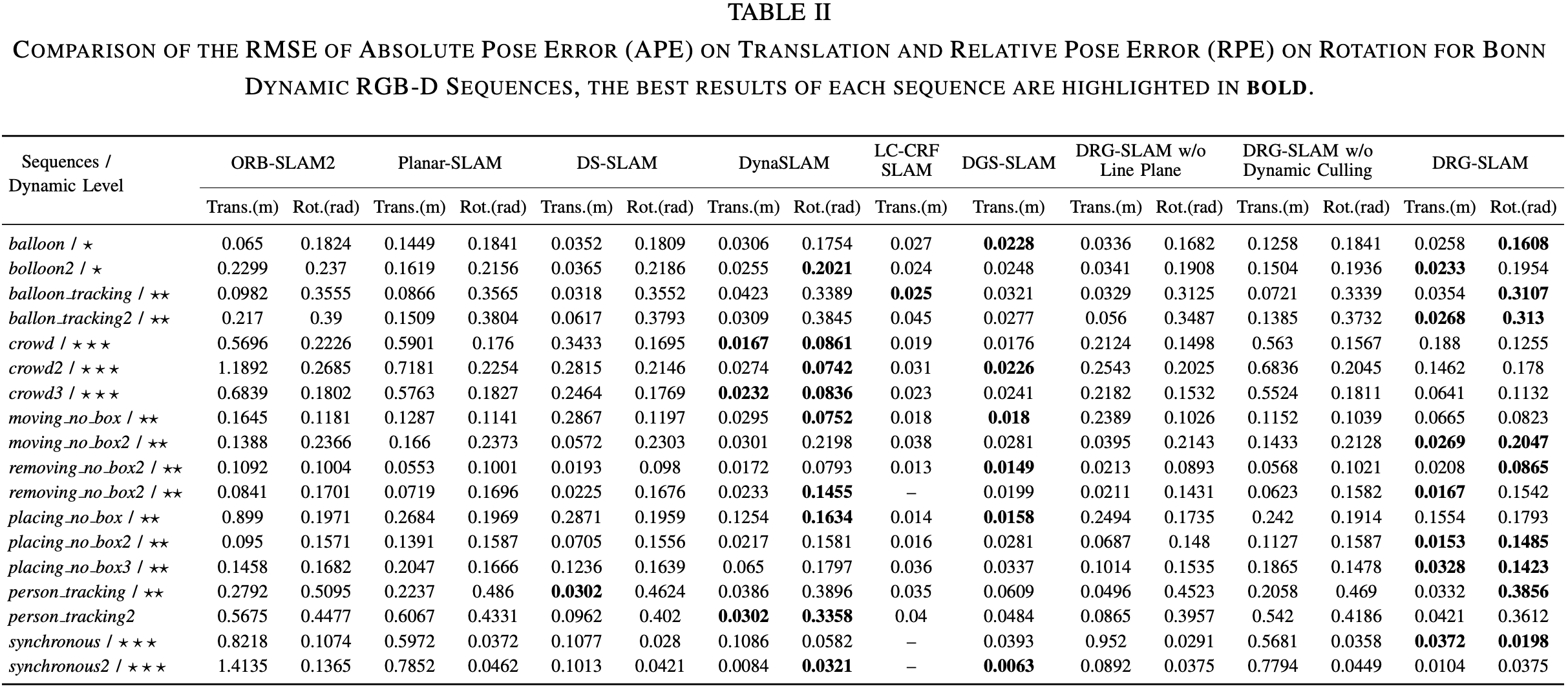
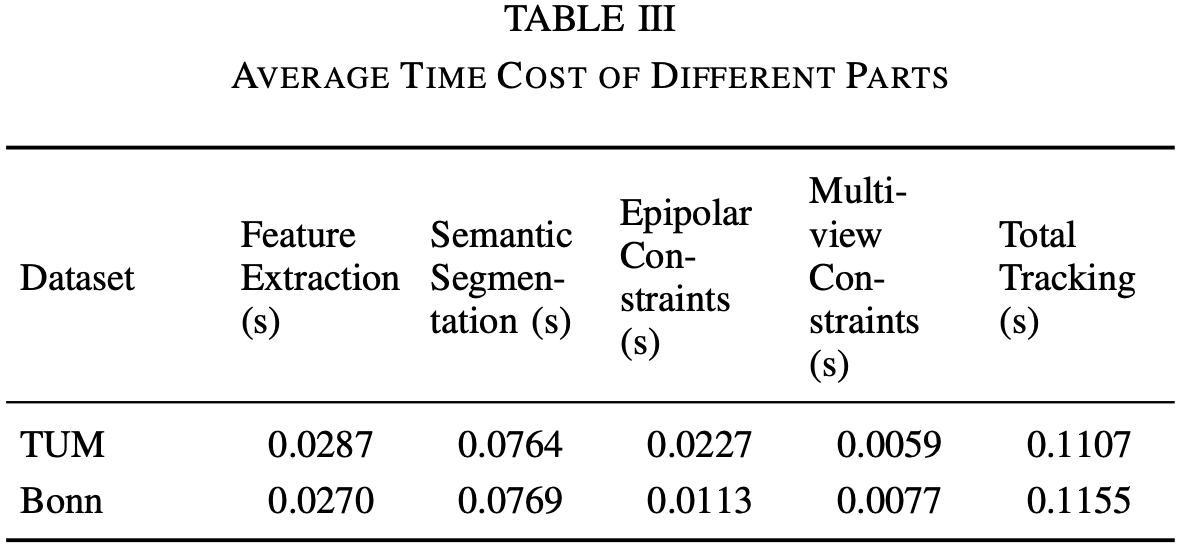
数据集:TUM RGB-D,Bonn RGB-D
硬件:i7-10750H @ 2.6GHz * 12,RTX 2060,16GB RAM
DRG-SLAM 基于 ORB-SLAM2 开发
考虑引入其他传感器数据,如 IMU;
动态物体被用于追踪而不是直接剔除;
创建环境的语义图。
[1] R. Grompone von Gioi, J. Jakubowicz, J.-M. Morel, and G. Randall, “LSD: A Fast Line Segment Detector with a False Detection Control,” IEEE Transactions on Pattern Analysis and Machine Intelligence , vol. 32, no. 4, pp. 722–732, Apr. 2010.
[2] L. Zhang and R. Koch,“An efficient and robust line segment matching approach based on LBD descriptor and pairwise geometric consistency,” Journal of Visual Communication and Image Representation , vol. 24, no. 7, pp. 794–805, Oct. 2013.
[3] C. Feng, Y. Taguchi, and V. R. Kamat, “Fast plane extraction in organized point clouds using agglomerative hierarchical clustering,” in 2014 IEEE International Conference on Robotics and Automation (ICRA) . IEEE, 2014, pp. 6218–6225.
[4] V. Badrinarayanan, A. Kendall, and R. Cipolla, “SegNet: A Deep Convolutional Encoder-Decoder Architecture for Image Segmentation,” IEEE Transactions on Pattern Analysis and Machine Intelligence , vol. 39, no. 12, pp. 2481–2495, Dec. 2017.
[5] Y. Zhou, L. Kneip, C. Rodriguez, and H. Li, “Divide and Conquer: Efficient Density-Based Tracking of 3D Sensors in Manhattan Worlds,” in Computer Vision – ACCV 2016 , S.-H. Lai, V. Lepetit, K. Nishino, and Y. Sato, Eds. Cham: Springer International Publishing, 2017, vol. 10115, pp. 3–19.