Dynamic SLAM-The Need For Speed

Posted on Edited on In Waline:

关于论文 Dynamic SLAM: The Need For Speed (ICRA, 2020) 的阅读总结。

Dynamic SLAM: The Need For Speed

论文情况

  • 标题：Dynamic SLAM: The Need For Speed
  • 作者：Mina Henein, Jun Zhang, Robert Mahony and Viorela Ila
  • 期刊：ICRA 2020
  • 源码：https://github.com/halajun/VDO_SLAM（与 VDO-SLAM 出自同一个组）

1 Introduction

大量 SLAM 问题基于静态世界假设，这限制了现存算法在包含动态物体的真实世界的精确度。

DL 的发展提供了几乎实时目标检测和分割的可靠算法：

  • 将 DL 融入几何 SLAM，除了检测和分割，还需要 3D 模型是可用的，或者前段显示提供对象的位姿。对 3D 模型的精确度要求限制了潜在的应用领域。
  • 同时，多目标跟踪和 3D 位姿仍然是一大挑战。需要一种算法，可以利用现有 DL 强大的检测和分割能力，而不依赖额外的位姿估计或运动模型先验。

本文提出来一个无模型、目标感知的基于点的动态 SLAM 模型：

  • 利用基于图像的语义信息进行机器人定位、绘制静态结构、估计动态物体的完整 SE(3)SE(3) 位姿变换、构建世界的动态表示。
  • 利用物体的刚体运动来提取场景中物体的速度信息，如 Fig.1。

本文关键创新：

  • 一种新颖的姿态变化表示，用于对给定刚体上点集合的运动进行建模，并将模型集成到 SLAM 优化框架。只要对象的语义检测和分割可以被跟踪，生成的模型与对象的底层 3D 模型无关。
  • 本文是第一个能够估计相机位姿、静态和动态结构、场景中每个刚性物体的完整 SE(3)SE(3) 位姿变化的工作。

2 Accounting for Dynamic Obects in SLAM

问题描述：SLAM 下机器人的感知范围内存在相对较大的动态刚体。SLAM 前端能在不同时刻识别并提取同一物体上的点，这些点共享在一个潜在运动约束上，用于提高 SLAM 性能。

2.1 Problem Formulation

动态物体 SLAM：

  • 使用因子图，获取静态和动态 3D 结构、位姿变换约束。

考虑高斯噪声，问题变为非线性最小二乘问题：

  • 机器人位姿 x={x0,...,xnx},xk∈SE(3),k∈{0,...,nx}\pmb{x} = \{ x_0, ..., x_{n_x} \}, x_k \in SE(3), k \in \{ 0, ..., n_x \}，其中 nxn_x 为时间步数量；
  • 不同时间步环境中的 3D 点特征 l={l01,...,lnxnl},lki∈R3\pmb{l} = \{ l_0^1, ..., l_{n_x}^{n_l} \}, l_k^i \in \mathbb{R}^3，其中i∈{1,...,nl}i \in \{ 1, ..., n_l \} 为 landmark 的唯一索引，nln_l 为检测到的 landmark 的总数。l=ls∪ld\pmb{l} = \pmb{l_s} \cup \pmb{l_d} 包含静态 landmark 集合 ls\pmb{l_s} 和动态 landmark 集合 ld\pmb{l_d}。
  • 一个运动目标在不同时间的同一个点用不同的变量表示，即 lk−1il_{k-1}^i 和 lkil_k^i，即不同时间步的第 ii 个特征点。

2.2 Motion Model of a Point on a Rigid Body

2.2.1 符号设定

符号：

  • 设 {0}\{ 0 \} 为参考坐标系（世界坐标系），{L}\{ L \} 为运动刚体的坐标系。

  • 0Lk∈SE(3){}^0 L_k \in SE(3) 为刚体相对坐标系 {0}\{ 0 \} 的位姿。

  • 对于物体上的特征点，Lli∈R3{}^L l^i \in \mathbb{R}^3 表示点在该物体坐标系的坐标。记 0lki{}^0 l_k^i 为同一个特征点在时间步 kk 相对于坐标系 {0}\{0\} 的坐标。

  • 注意，对运动中对刚体来说，Lli{}^L l^i 是常量，0Lk,0lki{}^0 L_k, {}^0 l_k^i 则是随时间变化的。存在关系：

    Llˉi=0Lk−10lˉki(1){}^L \bar{l}^i = {}^0 L_k^{-1} {}^0\bar{l}_k^i \tag{1}

    其中 lˉ\bar{l} 为齐次坐标。

2.2.2 坐标系变化之间的关系

物体 LL 从 k−1k-1 到 kk 到相对变换表示为 k−1Lk−1Hk∈SE(3){}^{L_{k-1}}_{k-1} H_k \in SE(3)，成为 body-fixed 坐标位姿系变换，且存在关系：

k−1Lk−1Hk=0Lk−1−10Lk(2){}_{k-1}^{L_{k-1}} H_k = {}^0 L_{k-1}^{-1} {}^0 L_k \tag{2}

Fig.2a 表示了三个连续位姿的上述关系：

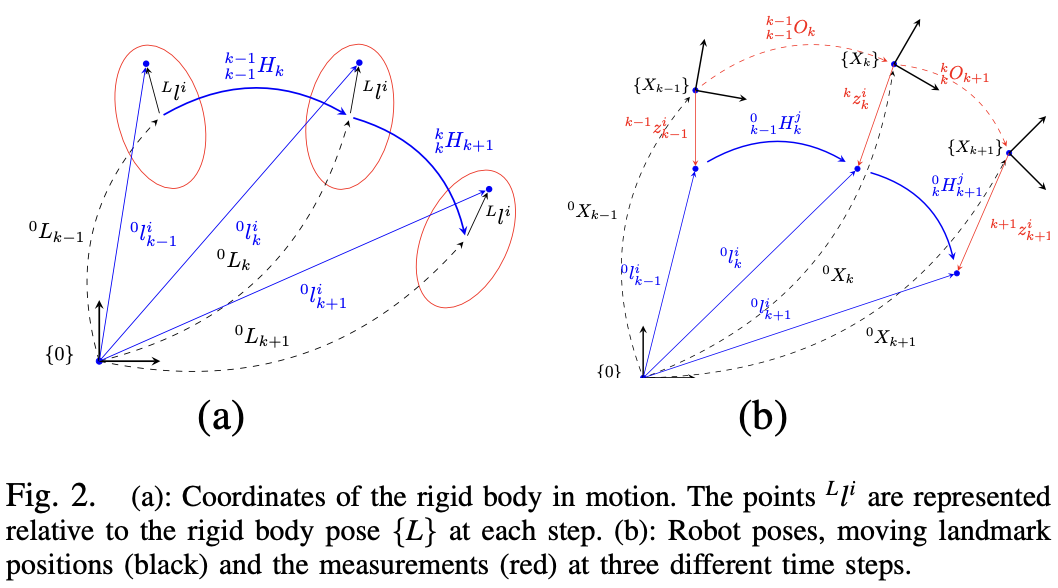
由 (2) 可以得到心得刚体坐标可以写为增量形式：

0Lk=0Lk−1k−1Lk−1Hk(3){}^0 L_k = {}^0 L_{k-1} {}_{k-1}^{L_{k-1}} H_k \tag{3}

考虑物体坐标系 {L}\{ L \} 中的点 Lli{}^L l^i，联合 (1) (3) 可以得到：

0lˉki=0Lk−1k−1Lk−1Hk0Lk−1−10lˉk−1i(4){}^0 \bar{l}_k^i = {}^0 L_{k-1} {}_{k-1}^{L_{k-1}} H_k {}^0 L_{k-1}^{-1} {}^0\bar{l}_{k-1}^i \tag{4}

由 (4) 可以得到 k−10Hk=0Lk−1k−1Lk−1Hk0Lk−1−1∈SE(3){}^0_{k-1}H_k = {}^0 L_{k-1} {}_{k-1}^{L_{k-1}} H_k {}^0 L_{k-1}^{-1} \in SE(3)，表示了位姿变换的坐标系变化，并说明了 (2) 中 body-fixed 坐标系的坐标系变化与参考坐标系的坐标系变化之间的关系。从而有：

0lˉki=k−10Hk0lˉk−1i(5){}^0 \bar{l}_k^i = {}^0_{k-1}H_k {}^0\bar{l}_{k-1}^i \tag{5}

(5) 是本文方法的关键点，其限制了对物体位姿 0Lk{}^0 L_k 估计的必要性，允许直接使用参考坐标系中的点 lˉki\bar{l}_k^i。

2.2.3 线速度提取

给定刚体在惯性坐标系下的位姿变换 k−10Hk{}_{k-1}^0 H_k，刚体的线速度向量为：

v=k−10tk−(I3−k−10Rk)ck−1(6)v = {}_{k-1}^0 t_k - (I_3 - {}_{k-1}^0 R_k) c_{k-1} \tag{6}

其中 k−10Rk∈SO(3){}_{k-1}^0 R_k \in SO(3) 和 k−10tk∈R3{}_{k-1}^0 t_k \in \mathbb{R}^3 表示刚体位姿变换 k−10Hk{}_{k-1}^0 H_k 的旋转和平移，I3I_3 为单位矩阵，ck−1c_{k-1} 为刚体在 k−1k-1 时的质心坐标。

由于算法设计，并没有直接获取物体的质心，而是近似为物体上检测到的特征点的 3D 质心。(6) 的详细推导参考 [1]。

2.3 Motion Factors in Dynamic SLAM

为了估计了相机位姿、静态和动态结构、动态结构的运动，运动因子和从机器人本体传感器获得的里程数，以及 landmark 观测被联合优化：

θ∗=argmin⁡θ{∑k=1mkρh((h(xk,lki)−zki)⊤Σwk−1(h(xk,lki)−zki))+∑i=1miρh((f(xk−1,xk)−ok)⊤Σvk−1(f(xk−1,xk)−ok))+∑i,jmsρh((g(lk−1i,lki,k−10Hkj))⊤Σq−1(g(lk−1i,lki,k−10Hkj))}θ=x∪l∪H\begin{aligned} \boldsymbol{\theta}^*&=\underset{\boldsymbol{\theta}}{\operatorname{argmin}}\left\{\sum_{k=1}^{m_k} \rho_h\left(\left(h\left(x_k, l_k^i\right)-z_k^i\right)^{\top} \Sigma_{w_k}^{-1}\left(h\left(x_k, l_k^i\right)-z_k^i\right)\right)+\right. \\ &\sum_{i=1}^{m_i} \rho_h\left(\left(f\left(x_{k-1}, x_k\right)-o_k\right)^{\top} \Sigma_{v_k}^{-1}\left(f\left(x_{k-1}, x_k\right)-o_k\right)\right)+ \\ &\sum_{i, j}^{m_s} \rho_h\left(\left(g\left(l_{k-1}^i, l_k^i,{ }_{k-1}^0 H_k^j\right)\right)^{\top} \Sigma_q^{-1}\left(g\left(l_{k-1}^i, l_k^i,{ }_{k-1}^0 H_k^j\right)\right)\right\} \\ \pmb{\theta} &= \pmb{x} \cup \pmb{l} \cup \pmb{H} \end{aligned}

H\pmb{H} 表示描述物体运动的变量集合。

其中（参考 Fig.2b 中红线）：

  • ρh\rho_h 为 Huber 函数；

  • h(xk,lki)h(x_k, l_k^i) 为 3D 点测量模型，Σwk\Sigma_{w_k} 为点测量协方差，z={z1,...,zmk},zk∈R3\pmb{z} = \{ z_1, ..., z_{m_k} \}, z_k \in \mathbb{R}^3 表示所有的时间步下的 mkm_k 个 3D 点测量；

  • f(xk−1,xk)f(x_{k-1}, x_k) 为惯导模型，Σvk\Sigma_{v_k} 为惯导协方差，o={o1,...,omi}\pmb{o} = \{ o_1, ..., o_{m_i} \} 表示 mim_i 个惯导测量；

  • g(lk−1i,lki,k−10Hkj)g\left(l_{k-1}^i, l_k^i,{ }_{k-1}^0 H_k^j\right) 表示动态物体上的点点运动模型，Σq\Sigma_q 为运动协方差，msm_s 为所有的运动因子的数量。被检测到的刚体 jj 上的任意点的运动可以使用 (5) 表述为：

    g(lk−1i,lki,k−10Hkj)=0lk−1i−k−10Rkj0lk−1i−k−10tkj+qsj(8)g\left(l_{k-1}^i, l_k^i,{ }_{k-1}^0 H_k^j\right)={ }^0 l_{k-1}^i-{ }_{k-1}^0 R_k^{j 0} l_{k-1}^i-{ }_{k-1}^0 t_k^j+q_{s_j} \tag{8}

    其中 qs∼N(0,Σq)q_s \sim \mathcal{N}(0, \Sigma_q) 为高斯噪声

(8) 中的因子为三元因子（Fig.3 中橙色因子），成为刚体上点的运动模型。

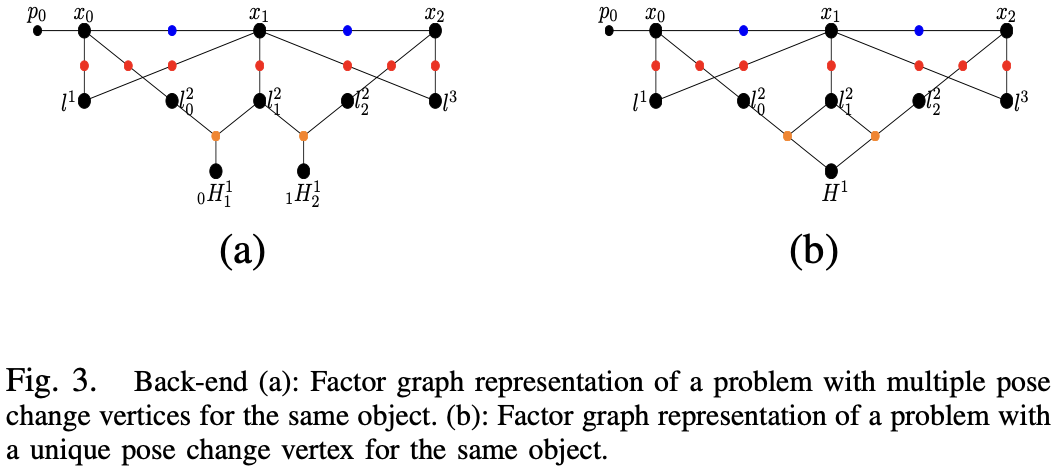
2.4 The Fractor Graph

本文评估了使用/没使用恒定运动（constant motion）模型的场景：

  • 城市场景：当物体的运动受到变化（加速、减速等）的影响时，运动建模是具有挑战性的。因此，允许在每个时间步上估计一个新的位姿变化。Fig.3a 为这种情况的因子图，途中使用两个运动顶点对两个不同的时间过渡估计同一物体的运动。一种约束是最小化这些运动估计之间的变化。
  • 高速公路：每个物体（车辆）保持恒定运动，如 Fig.3b。

进一步，如果 body-fixed 坐标系的位姿变化是恒定的，那么参考坐标系的位姿变化也是恒定的。对于任意 k−1k-1 和 k′−1k'-1，则：

k−1Lk−1Hk=C=k′−1Lk′−1Hk′∈SE(3)(9){}_{k-1}^{L_{k-1}} H_k = C ={}_{k'-1}^{L_{k'-1}} H_{k'} \in SE(3) \tag{9}

用 (9) 替换 (3) 得到 0Lk=0Lk−1C{}^0 L_k = {}^0 L_{k-1} C，且有 k−10Hk=0Lk−1C0Lk−1−1{}^0_{k-1}H_k = {}^0 L_{k-1} C {}^0 L_{k-1}^{-1}，则：

k−10Hk=0LkC0Lk−1=k0Hk+1(10){}^0_{k-1}H_k = {}^0 L_{k} C {}^0 L_{k}^{-1} = {}^0_k H_{k+1} \tag{10}

这说明对于物体 jj 和任意时间 k,k′k, k'，有 k−10Hkj=0Hj=k′0Hk′+1j∈SE(3){}^0_{k-1}H_k^j = {}^0 H^j = {}^0_{k'} H^j_{k'+1} \in SE(3)。

3 System Overview

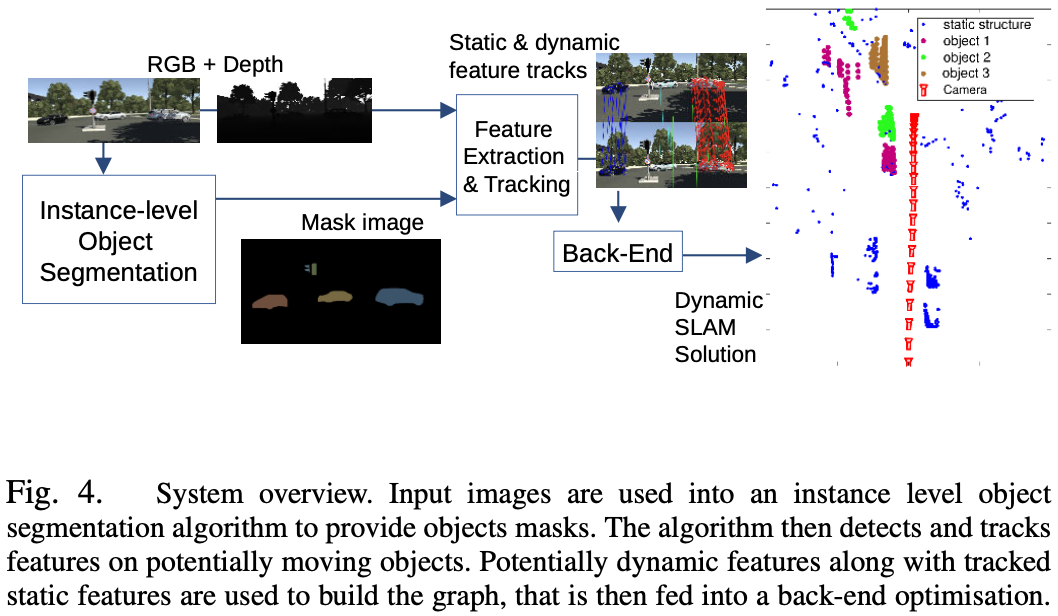
Fig.4 中设机器人携带 RGB-D 相机以及惯性传感器（里程计，IMU）。

为了保证运动物体上的特征被检测到，使用一个实例级的物体分割算法来产生物体掩码。前端利用物体掩码来检测潜在移动物体和静态背景上的特征。SLAM 前端通过目标分割和特征跟踪，识别和关联同一刚体对象上不同时间步的点。这些点共享一个基本的运动模型，利用这个模型来实现同步定位、映射和移动对象跟踪。

静态和动态三维测量以及本体感知传感器的测量被集成到后端，以同时估计摄像机运动、静态和动态结构以及场景中被检测对象的 SE(3) 位姿转换。

4 Experiments and Results

  • 误差度量：
    • 相对平移误差 RTE；
    • 相对旋转误差 RRE；
    • 相对结构误差 RSE（所有静态和动态结构 landmark 在预测和 GT 中的位置误差）；
    • 物体运动平移误差 OMTE，物体运动旋转误差 OMRE，物体运动速度误差 OMSE。
  • 数据集 KITTI 上的评估：只对分割掩码达到一定比例的目标进行估计，确保排除了远处和部分观察到的进入/离开相机视野的物体。对于 vKITTI，阈值设置为 6%，对于 KITTI 设置为2%。

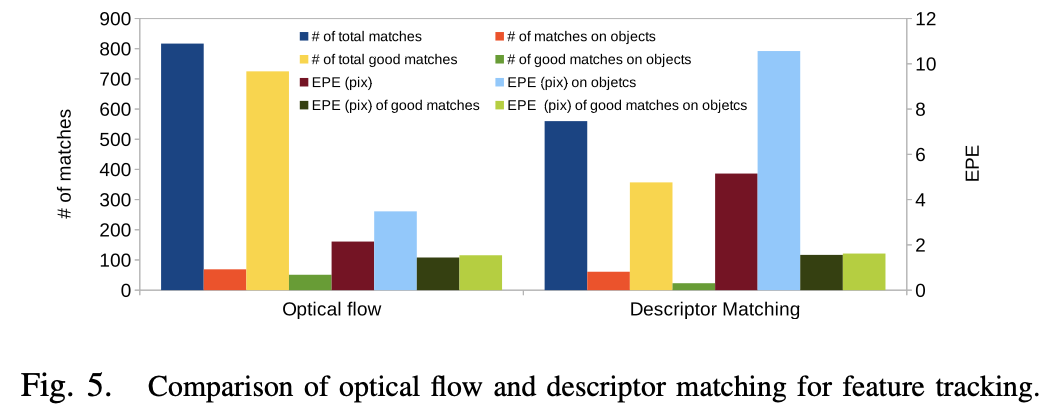
特征跟踪误差如 Fig.5，使用 PWC-Net 和特征描述子匹配，评价标准为 end-point error（EPE）：

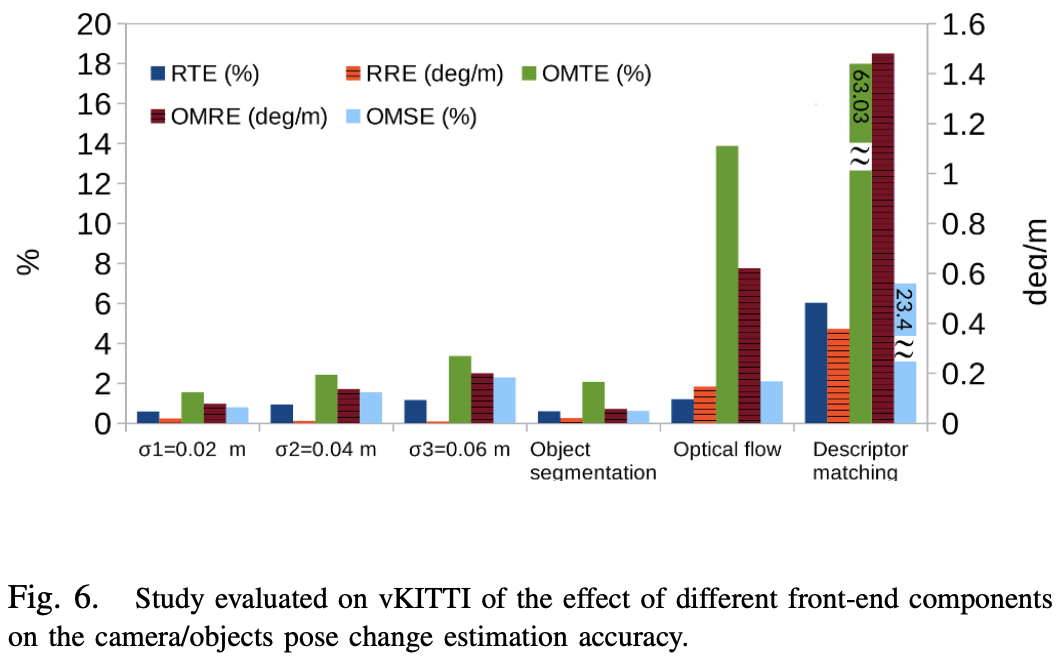
在观测的每个轴上分别添加 0 均值，标准差 σ1=0.02,σ2=0.04,σ3=0.06m\sigma_1 = 0.02, \sigma_2 = 0.04, \sigma_3 = 0.06m 的高斯噪声，不同前端组件对相机位姿变换的预测准确率如 Fig.6：

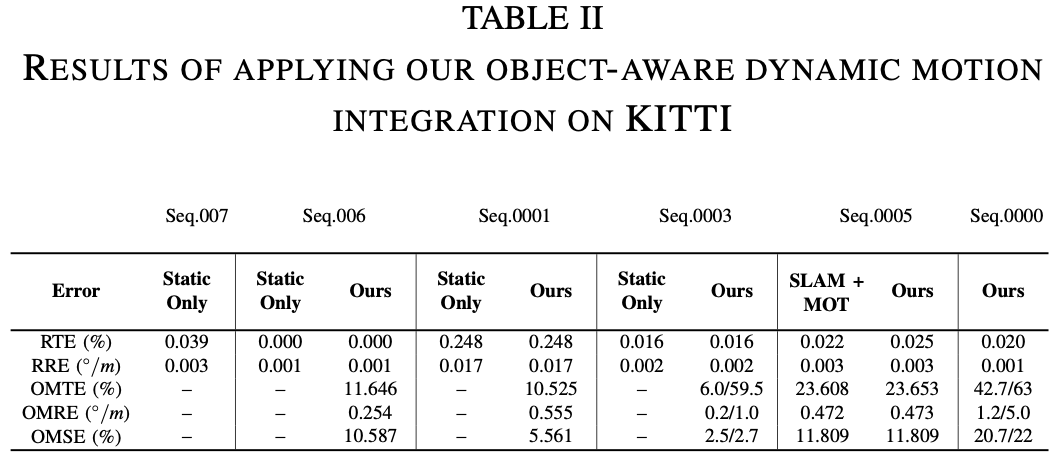
在 KITTI 上的实验结果如 Table II，Static Only 表示不考虑场景中的动态物体：

附录

为证明 (6) 等价于在 {0}\{ 0 \} 处观测到的从时间 k−1k-1 到 kk 物体位姿原点到平移，先进性如下的变换：

k−10Hk=0Lk−1k−1Lk−1Hk0Lk−1−1=0Lk0Lk−1−1(11){}^0_{k-1}H_k = {}^0 L_{k-1} {}_{k-1}^{L_{k-1}} H_k {}^0 L_{k-1}^{-1} = {}^0 L_k {}^0 L_{k-1}^{-1} \tag{11}

设 0RLk−1∈SO(3){}^0 R_{L_{k-1}} \in SO(3) 和 0tLk−1∈R3{}^0 t_{L_{k-1}} \in \mathbb{R}^3 为 0Lk−1{}^0 L_{k-1} 中的旋转和平移，则 k−10Hk{}^0_{k-1}H_k 的平移和旋转可以表示为 0tLk−0RLk0RLk−1⊤0tLk−1{}^0 t_{L_{k}} - {}^0 R_{L_{k}}{}^0 R_{L_{k-1}}^\top {}^0 t_{L_{k-1}} 和 RLk0RLk−1⊤R_{L_{k}}{}^0 R_{L_{k-1}}^\top。将这两个式子带入 (6) 得到：

v=0tLk−0RLk0RLk−1⊤0tLk−1−(I3−0RLk0RLk−1⊤)0tLk−1(12)v = {}^0 t_{L_{k}} - {}^0 R_{L_{k}}{}^0 R_{L_{k-1}}^\top {}^0 t_{L_{k-1}} - (I_3 - {}^0 R_{L_{k}}{}^0 R_{L_{k-1}}^\top) {}^0 t_{L_{k-1}} \tag{12}

最后化简得 v=0tLk−0tLk−1v = {}^0 t_{L_{k}} - {}^0 t_{L_{k-1}}。

参考

  • [1] G. S. Chirikjian, R. Mahony, S. Ruan, and J. Trumpf, “Pose changes from a different point of view,” in Proceedings of the ASME International Design Engineering Technical Conferences (IDETC) 2017. ASME, 2017.