Hungarian Algorithm

Posted on 2022-06-17 Edited on 2022-11-19 In Paper Note Waline:

对论文 IMLS-SLAM: Scan-to-Model Matching Based on 3D Data (ICRA, 2022) 的阅读整理。

IMLS-SLAM

论文情况

题目：IMLS-SLAM: Scan-to-Model Matching Based on 3D Data
期刊/会议：ICRA 2018
作者：Jean-Emmanuel Deschaud

1 预备知识

1.1 一种直接获得法向量的方法

来自论文：Fast and Accurate Computation of Surface Normals from Range Images
论文简述：论文提出一种通过对来自 Spherical Range Image（SRI）的表面求导，直接获得法向量的方法。
研究背景：在之前的研究中，要获得一个点的切平面或者法向量，都是对该点的邻域采用最小二乘法，但是该方法计算代价昂贵。而在研究一个点的切平面或者法向量时，该点一定不是一个孤独的点，附近一定有邻域点。
具体推理流程：
- 定义球面坐标系中一点 $m=(r,\theta,\varphi)^T$ ，其对应着笛卡尔坐标系一点 $p=(x,y,z)^T$
- 某一点的切平面与法向量为：
  - 切平面： $n_x x + n_y y + n_z z + d = 0$ 或 $p^T n +d = 0$
  - 法向量： $n = (n_x, n_y, n_z)^T,\ ||n||_2^2 = 1$
- SRI 定义：是一个函数 $s(\theta,\varphi)$ ，指从坐标系原点出发，沿着 $(\theta,\varphi)$ 方向，深度为 $r(=s(\theta,\varphi))$ 的某一点。
- Fast Approximate Least Squares：
  
  首先，确定球面坐标系与笛卡尔坐标系之间的转换关系（此处 $\varphi$ 为向量与 xOy 平面的夹角）：
  
  $p = \left[ \begin{matrix} x \\ y \\ z \end{matrix} \right] = r \left[ \begin{matrix} \cos \theta \cos \varphi \\ \sin \theta \cos \varphi \\ \sin \varphi \end{matrix} \right] \\ m = \left[ \begin{matrix} r \\ \theta \\ \varphi \end{matrix} \right] = \left[ \begin{matrix} \sqrt{x^2 + y^2 + z^2} \\ \arctan(x/z) \\ \arcsin (y / \sqrt{x^2 + y^2 + z^2}) \end{matrix} \right]$
  
  设 $v=(\cos \theta \cos \varphi, \sin \theta \cos \varphi, \sin \varphi)^T$ ，则上面的式子可以表示为 $p = rv$ 。目标优化的损失函数是尽量使得点都满足平面约束方程，即找到 $n$ 和 $d$ 使得在领域内的点 $p_i$ 满足：
  
  $\min e=\sum_i (p_i^T n - d)^2$
  
  用来自 Unconstrained Least Squares 的思路：
  1. 对目标函数两侧除以 $d^2$ ：
  $\tilde{e} = \sum_i (p_i^T \tilde{n} - 1)^2$
  1. 用 $p=rv$ 替换上式，把 $r_i$ 提出到括号外：
  $\tilde{e} = \sum_i r_i^2 (v_i^T \tilde{n} - r_i^{-1})^2$
  1. 默认同一个邻域内的点深度 $r_i$ 都近似相等，因此可以进一步简化：
  $\tilde{e} = \sum_i (v_i^T \tilde{n} - r_i^{-1})^2$
  1. 使用最小二乘思想或者下式即可求解（上式对 $\tilde{n}$ 求一阶导并取 0 可以得到下面的式子）：
  $\tilde{M} = \sum_i v_i v_i^T, \ \tilde{b} = \sum_i \frac{v_i}{r_i} \\ \tilde{n} = \tilde{M}^{-1} \tilde{b}$
- 使用 SRI 方法：
  1. 设 DEL 算子（Nabla 算子）在笛卡尔坐标系下为下式，其中 $e_x,e_y,e_z$ 分别对应 x，y，z 轴上的单位向量：
  $\nabla = e_x \frac{\partial}{\partial x} + e_y \frac{\partial}{\partial y} + e_z \frac{\partial}{\partial z} = (\frac{\partial}{\partial x}, \frac{\partial}{\partial y}, \frac{\partial}{\partial z})^T$
  1. 由前笛卡尔坐标系和球面坐标系的关系，可以得到 $x = g(r,\theta,\varphi)$ ， $g(\cdot)$ 为一个转换函数，则：
  $\begin{aligned} \frac{\partial}{\partial x} &= \frac{\partial}{\partial r} \frac{\partial r}{\partial x} + \frac{\partial}{\partial \theta} \frac{\partial \theta}{\partial x} + \frac{\partial}{\partial \varphi} \frac{\partial \varphi}{\partial x} \\ &= \frac{2x}{2 \sqrt{x^2 + y^2 + z^2}} \frac{\partial}{\partial r} + \frac{- \frac{y}{x^2}}{1 + (\frac{y}{x})^2} \frac{\partial}{\partial \theta} + \frac{2x}{2 \sqrt{x^2 + y^2} (1 + (\frac{\sqrt{x^2 + y^2}}{z})^2)} \frac{\partial}{\partial \varphi} \\ &= \frac{x}{r} \frac{\partial}{\partial r} + \frac{-y}{x^2 + y^2} \frac{\partial}{\partial \theta} + \frac{xz^2}{\sqrt{x^2 + y^2}(x^2 + y^2 + z^2)} \frac{\partial}{\partial \varphi} \\ &= \cos \theta \cos \varphi \frac{\partial}{\partial r} + \frac{-\sin \theta}{r \cos \varphi} \frac{\partial}{\partial \theta} + \frac{\cos \theta \sin \varphi}{r} \frac{\partial}{\partial \varphi} \end{aligned}$
  
  同理可以计算 $\frac{\partial}{\partial y}$ 和 $\frac{\partial}{\partial z}$ 。
  1. 有了算子 $\nabla$ ，则可以对 $r=s(\theta,\varphi)$ 求导，由 SRI 函数的定义，可知此导数即为所求法向量（类似于梯度）：
  $n = \nabla s(\theta,\varphi)$

1.2 点云局部集合结构具有以下三种性质

来自论文：Dimensionality based Scale Selection in 3D Lidar Point Clouds
对点云点集的协方差矩阵进行 PCA 主成分析，得到 3 个特征值 $a_{1D}, a_{2D}, a_{3D}$ 分别对应下列三种性质：
1. 线性性（linear）：线性性大于其他两个性质。
2. 平面性（planar）：平面性最突出。
3. 空间性（volumetric）：如果形成一个弥合球面，则点云具有空间性。
实现细节：
获取点 $p$ 的邻域点云 $V_p^r$ ，使得：

$||p - p_k|| \le r,\ \mathrm{where}\ p_k \in V_p^r$
1. $r$ 如何选取？
给定一个 $r$ 的上下界，采样边界中的 16 个值，对比发现使得 $V_p^r$ 熵最小化的 $r$ 就是最优半径，此处熵的计算公式为：

$\mathrm{Ef} (V_p^r) = -a_{1D} \ln (a_{1D}) - a_{2D} \ln (a_{2D}) - a_{2D} \ln (a_{2D})$
1. 如何计算 $a_{1D}, a_{2D}, a_{3D}$ ？（利用 PCA 计算）
假设现在获取了一个邻域点云，首先对点去质心得到 $M$ ，即：

$M = (x_1 - \bar{x}, \cdots, x_N - \bar{x})$

计算特征矩阵：

$C = \frac{1}{N} M^T M$

对该矩阵进行特征分解可以得到特征值的开根 $\sigma_1, \sigma_2, \sigma_3\ (\sigma_i = \sqrt{\lambda_i})$ （从小到大排列），从而可以得到：

$\begin{aligned} a_{1D} &= \frac{\sigma_1 - \sigma_2}{\sigma_1} \\ a_{2D} &= \frac{\sigma_2 - \sigma_3}{\sigma_1} \\ a_{3D} &= \frac{\sigma_3}{\sigma_1} \end{aligned}$

注意，最后一定满足 $a_{1D} + a_{2D} + a_{3D} = 1$ 。

2 MLS（移动最小二乘法，Moving Least Squares）

出自论文：Mesh-Independent Surface Interpolation
移动最小二乘法（MLS，Moving Least Squares）是建立大量离散数据拟合曲线的理想方法。当大量离散数据的分布较为杂乱时，使用传统的最小二乘法，往往需要对数据进行分段拟合，此外还要避免相邻分段上的拟合曲线不连续不平滑的问题。而 MLS 在处理相同问题时则不需要上述这些繁琐的步骤，简单易于实现。

在 MLS 法中，需要在一组不同位置的节点（node）附近建立拟合曲线，每个节点都有自己的一组系数 $a_j(x_{node})$ 用于定义该位置附近拟合曲线的形态。因此，在计算某个节点附近的拟合曲线（曲面）时，只需要计算该点的该组系数值 $a_j$ 即可。

此外，每个节点的系数 $a_j$ 取值只考虑其临近采样点，且距离节点越近的采样点贡献越大，对于位置较远的点则不予考虑。

2.1 拟合函数

相比于传统最小二乘法，MLS 法中的拟合函数不是一个多项式，而是一组系数向量函数 $a_j(x)$ 和 $p_j(x)$ ，其中 $x$ 为空间坐标。

某个节点 node 附近的拟合函数为 $u_{node}(x)$ ，具体定义为：

$u_{node}(x) = \sum_{j=1}^m a_j(x_{node}) * p_j(x)$

其中， $x_{node}$ 为节点的空间坐标， $x$ 为节点 node 附近的某一个位置坐标， $a_j$ 即为用于定义节点 node 附近拟合曲线（曲面）的一组系数， $p_j(x)$ 则是一组基函数， $m$ 为基函数个数，常用形式如下：

空间维度	一阶形式	二阶形式
1 维： $\pmb{x} = (x)$	$p_1 = 1,\ p_2 = x$	$p_1 = 1,\ p_2 = x,\ p_3 = x^2$
2 维： $\pmb{x} = (x,y)$	$p_1 = 1,\ p_2 = x,\ p_3 = y$	$p_1 = 1,\ p_2 = x,\ p_3 = y,$ $p_4 = xy,\ p_5 = x^2,\ p_6 = y^2$
3 维： $\pmb{x} = (x,y,z)$	$p_1 = 1,\ p_2 = x,\ p_3 = y,\ p_4 = z$	$p_1 = 1,\ p_2 = x,\ p_3 = y,\ p_4 = z,$ $p_5 = xy,\ p_6 = xz,\ p_7 = yz,$ $p_8 = x^2,\ p_9 = y^2,\ p_{10} = z^2$

MLS 法中，通过调整系数 $a$ ，使得节点 node 附近 $n$ 个采样点取值与拟合函数在采样点之间差的加权平方和最小，由此可以建立最优化模型 $J$ ：

$\begin{aligned} \min J &= \sum_{p=1}^n w(x_{node} - x_p) [u(x_{node}) - u_p]^2 \\ &= \sum_{p=1}^n w(x_{node} - x_p) [\sum_{j=1}^m a_j(x_{node}) * p_j(x) - u_p]^2 \\ &= \sum_{p=1}^n w(x_{node} - x_p) [\sum_{j=1}^m a_j^{node} * p_j(x) - u_p]^2 \end{aligned}$

其中， $x_{node}$ 为节点 node 的空间位置， $p$ 为采样点， $n$ 为采样点个数， $x_p$ 为采样点 $p$ 的空间位置， $u_p$ 为采样点 $p$ 的取值 $u(x_p)$ ，此处 $a_j^{node} = a_j(x_{node})$ 。

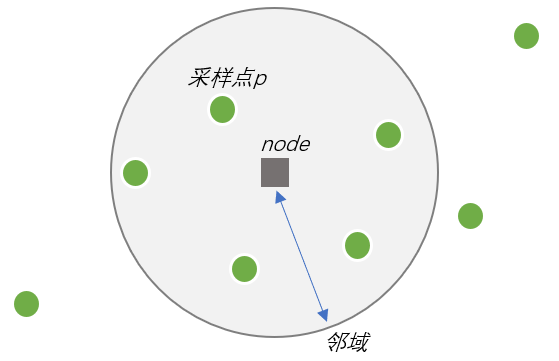图-1 MLS 采样点 p 和 node 的关系
上式中 $w$ 为权函数，保证距离 node 越近的采样点，对函数 $J$ 的贡献越大，常用形式如下（三次样条曲线）：

$w(x) = \operatorname{cubicspline}(x) = \begin{cases} \frac{1}{2} |x|^3 - |x|^2 + \frac{2}{3}, &|x| < 1 \\ \frac{1}{6} (2 - |x|)^3, &1 \le |x| < 2 \\ 0, &\mathrm{else} \end{cases}$

其中， $|x|$ 表示矢量 $x$ 的摸。当采样点 $p$ 与节点 node 的距离大于一定值时（上式中取 2），权重函数衰减为 0。
求解出在问题域上全部节点的系数，即可得到全域上的拟合曲线。

2.2 系数计算

由上述，每个节点 node 都有一组系数 $a_j(x_{node})$ 用于定义该位置附近拟合曲线（曲面）的形态，本部分介绍这个系数的具体求解方法。

已经获得了参数为系数 $a_j^{node}$ 的最优化模型 $J$ ，当 $J$ 取值最小时，则可获得节点 node 附近的拟合曲线（曲面） $u_{node}(x)$ 。
求解最优化模型最直接的方式即为求导：

$\frac{\partial J}{\partial a_i^{node}} = 2 \sum_{p=1}^{n} w(x_{node} - x_p) [\sum_{j=1}^m a_j^{node} * p_j(x) - u_p] p_i(x)$

当上式取 0 时， $J$ 取最小值，因此：

$\sum_{p=1}^n w(x_{node} - x_p) [\sum_{j=1}^m a_j^{node} * p_j(x) - u_p] p_i(x) = 0 \\ \sum_{p=1}^n w(x_{node} - x_p) \sum_{j=1}^m a_j^{node} * p_j(x) = \sum_{p=1}^n w(x_{node} - x_p) * u_p * p_i(x)$

引入下述符号简化表达：

$(p_i, p_j) = \sum_{p=1}^n w(x_{node} - x_p) * p_i(x) * p_j(x) \\ (u_p, p_j) = \sum_{p=1}^n w(x_{node} - x_p) * u_p * p_j(x)$

因此，可以将 $\frac{\partial J}{\partial a_i^{node}} = 0$ 整理为如下线性方程组，也称此方程组为法方程：

$\left[ \begin{matrix} (p_1, p_1) &\cdots &(p_1, p_j) &\cdots &(p_1, p_m) \\ \cdots \\ (p_i, p_1) &\cdots &(p_i, p_j) &\cdots &(p_i, p_m) \\ \cdots \\ (p_m, p_1) &\cdots &(p_m, p_j) &\cdots &(p_m, p_m) \end{matrix} \right] * \left[ \begin{matrix} a_1^{node} \\ \cdots \\ a_j^{node} \\ \cdots \\ a_m^{node} \end{matrix} \right] = \left[ \begin{matrix} (u_p, p_1) \\ \cdots \\ (u_p, p_j) \\ \cdots \\ (u_p, p_m) \end{matrix} \right]$

此方程组写成矩阵形式为 $Ma=b$ ，其中 $M$ 为基函数构成的系数矩阵， $a$ 表示 node 系数（未知数）向量，因此求解也变为 $a = M^{-1} b$ 。解此线性方程组，即可求解系数 $a_j^{node}$ 。
进一步，可以将任意位置上的拟合函数（ $\pmb{x}$ ）写为：

$u(\pmb{x}) = \sum_{j=1}^m a_j(\pmb{x}) * p_j(\pmb{x}) = P \cdot a = P \cdot M^{-1} \cdot b$

因此可以在任意点 $\pmb{x}$ 上计算出拟合函数及其取值。

2.3 拓展

MLS 法其实是一种广义的最小二乘法方法。MLS 法的核心优化模型 $J$ ：

$\begin{aligned} \min J &= \sum_{p=1}^n w [u(\pmb{x}) - u_p]^2 \\ &= \sum_{p=1}^n w(\pmb{x} - \pmb{x}_p) [\sum_{j=1}^m a_j (\pmb{x}) * p_j(\pmb{x}) - u_p]^2 \end{aligned}$

当权重函数 $w=1$ 时，则 MLS 方法退化为标准最小二乘法。对应 SLAM 中 ICP 算法，将 $u_p$ 视为 $\pmb{x}$ 需要对齐的地图上的点， $a_j (\pmb{x}) * p_j(\pmb{x})$ 视为对 $\pmb{x}$ 的位姿变换。
当权重函数为高斯函数或样条曲线时（如下图），则 MLS 退化为固定点最小二乘法（FLS，Fixed Least Squares）。

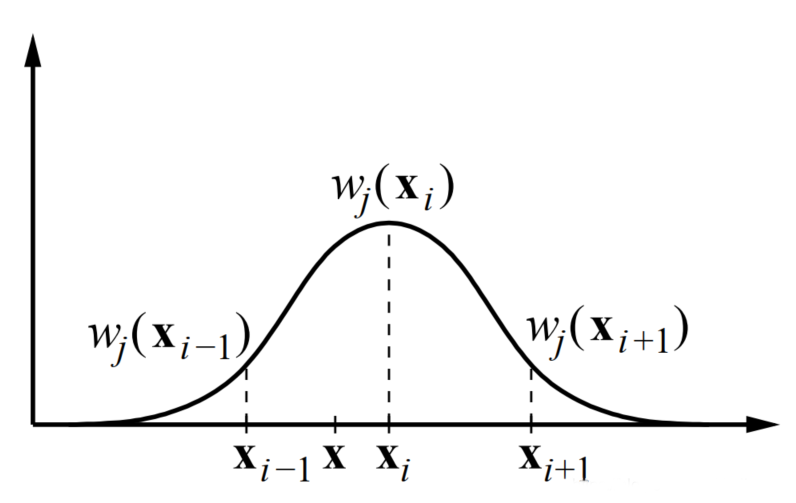图-2 权重函数为高斯函数
当权函数曲线为如下形式时，则 MLS 退化为多固定点最小二乘法（MFLS，Multiple Fixed Least Squares）。

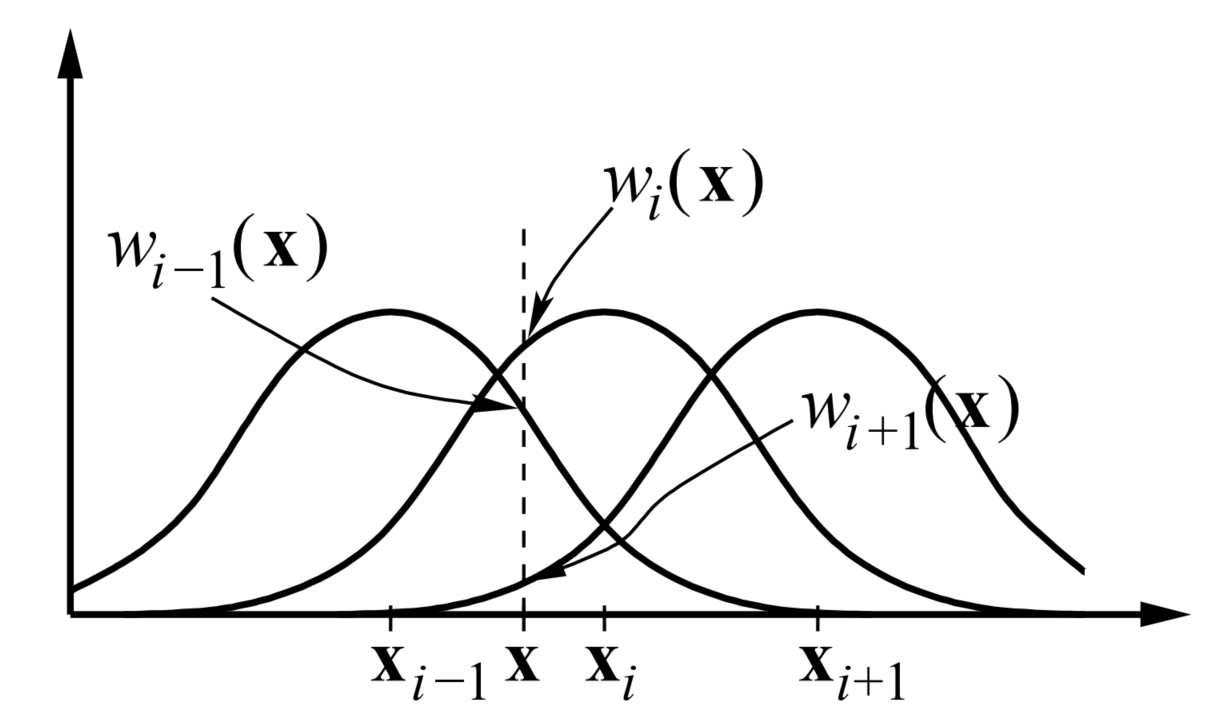图-3 权重函数较为复杂

3 Scan Egomotion and Dynamic Object Removal

3.1 Scan Egomotion

3.1.1 Egomotion

egomotion：The movement of the vehicle during the acquisition time of a scan.
egomotion 是指在获取激光雷达数据的过程中，vehicle 也在运动，这个过程有一个 movement（即 egmotion）需要补偿。

3.1.2 Scan Egomotion

由于数据获取过程中，vehicle 也在移动，因此需要在创建点云时考虑这个问题。
IMLS-SLAM 认为，上一次扫描结束的位姿 $T(t_{k-1})$ 和本次扫描结束的位姿 $T(t_k)$ 是线性关系，能够在 $t_{k-1} < t < t_k$ 这段时间内进行线性插值。
为获取局部无偏点云（Local Deskewed Point Cloud），需要估计当前时间 $t_k$ 的位姿 $\tilde{T}(t_k)$ ，考虑线性关系，假设两次扫描之间的位姿变换是相对相近的（即短时间内 vehicle 的运动是相对平滑且连续的），由于已经知道位姿 $T(t_i),\ i \le k-1$ ，则可以使用如下的求解方式：

$\because T(t_k) T(t_{k-1})^{-1} = T(t_{k-1}) T(t_{k-2})^{-1} = \Delta T \\ \therefore \tilde{T}(t_k) = T(t_{k-1}) T(t_{k-2})^{-1} T(t_{k-1})$

3.1.3 个人理解

如在 LOAM 中，构建局部无偏点云地图可能需要将扫描点云都投影到本次扫描的开始时刻（或结束时刻），此时就会使用到此次扫描开始时刻的位姿（上一次扫描结束的位姿）和此次扫描结束时刻的位姿之间的线性关系，即可能需要使用到此次扫描结束的位姿。
然而由于本轮扫描尚未结束，扫描点无法获取到位姿，因此可以使用 Scan Egomotion 的方式来解决这一问题。

3.2 Dynamic Object Removal

IMLS-SLAM 采用了一种暴力的方式去除存在动态可能性的物体，即认为一个大小为 $14m \times 14m \times 5m$ 的物体一定是动态的，需要去除。
具体去除方法：
1. 首先，使用一个容器存储地面点，并在原点云中去除这些点；
2. 使用聚类思想，只要相邻数据点之间的距离小于 $0.5m$ 就将它们聚集（cluster）在容器，形成一个 bounding box；
3. 如果形成的 bounding box 相对雷达坐标系三个坐标轴（ $X_v,Y_v,Z_v$ ）上的长度小于 $14m,14m,5m$ ，则认为 bounding box 中的物体为人、车等具有动态可能性的物体，因此丢弃此 bounding box 中的点。
4. 处理完所有 cluster 后，把地面点重新加回点云。
经过上面的方法，就除去了动态物体所对应的点。这一思想可能是认为激光雷达获得的数据点很多，因此尽管去除了大量点，也依然可以得到尽可能多的关键点，但是此种去除方法就先对较为暴力。

4 Scan Sampleing Strategy

4.1 提出原因

在之前的一些 ICP 版本中，提取点的特征时往往是先计算协方差矩阵，然后对矩阵计算特征值，根据特征值对特征分类，同时提取主轴方向，根据主轴方向和特征值进行点筛选。
IMLS-SLAM 不太认可这种方式，而是认为主轴方向为雷达的方向，直接把激光雷达的三个主轴作为点云的三个主轴。这样的话，大部分平面会直接被分配到每个轴上，比如地面就相当于沿着 z 轴观测，而一些物体立着的面就相当于沿着 x，y 轴发生移动。
其次，提取点是为了匹配得到位姿，不同的点对位姿精度的贡献不一样，如果能直接提取出对位姿贡献大的点，既可以很大程度上减少点的数量，又可以取得很好的精度。
所以，这个问题就演变成了，怎样去判断哪些点对位姿精度贡献大，对算法来讲，就是设计一些指标，去把这些点筛选出来。

4.2 采样步骤

使用前面的 SRI 求导法计算每一个点的法线，并使用 PCA 分析点云的三个特征值 $a_{1D}, a_{2D}, a_{3D}$ ；
提出了 9 个评价指标，其中前 6 个是点对 rotation 精度的贡献的定量评价，后 3 个是点对 translation 精度的贡献的定量评价：

$a_{2D}^2 (x_i \times n_i) \cdot X_v \\ -a_{2D}^2 (x_i \times n_i) \cdot X_v \\ a_{2D}^2 (x_i \times n_i) \cdot Y_v \\ -a_{2D}^2 (x_i \times n_i) \cdot Y_v \\ a_{2D}^2 (x_i \times n_i) \cdot Z_v \\ -a_{2D}^2 (x_i \times n_i) \cdot Z_v \\ a_{2D}^2 |n_i \cdot X_v| \\ a_{2D}^2 |n_i \cdot Y_v| \\ a_{2D}^2 |n_i \cdot Z_v|$

其中， $X_v, Y_v, Z_v$ 为局部地图下坐标轴的三个方向向量。
对每一个点都计算这 9 个指标，得到 9 个 list，对这 9 个 list 按照降序排序。
取每一个 list 中的第一个值所对应的点 $p_{Li}$ ，在这个点附近找 $s$ 个点，并遵循下列条件，其中 $r$ 为人为设定的参数：

$||p_{Li} - p_k|| < r,\ k = 1, 2, ..., s$
这样便得到 $9s$ 个点，即所寻找的点。

如下图中红色的点，即为经过此方法采样得到的点：

图-4 特征点采样（s = 100）

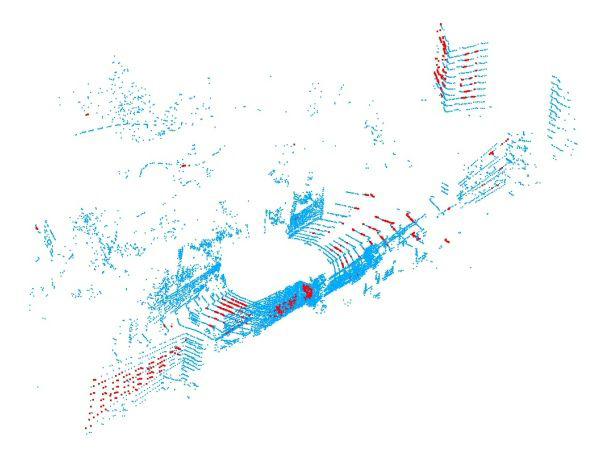
可以看到远离传感器中心的点可以更好地锁定旋转和大部分平面区域上点，以便更好地匹配。

5 Scan-to-Model Matching with IMLS Surface Representation

5.1 IMLS

在进行了数据采样后，就到了优化求解 $R, t$ 的部分，这里用到了 IMLS 方法（Provably Good Moving Least Squares）。
IMLS 起源于 MLS，仿照 MLS 构建了一个隐函数：

$I(x) = \frac{\sum_{s_i \in S} W_i(x) ((x - s_i) \cdot n_i)}{\sum_{s_i \in S} W_i(x)} \\ \mathrm{where}\ \ W_i(x) = \exp (-{\frac{||x - s_i||^2}{h^2}})$
- 其中 $W_i(x)$ 代表权重， $h$ 为 IMLS 模型的参数，与点云采样密度和噪声有关，隐函数 $I(x)$ 能够描述目标点到目标曲面的距离。观察此权重函数会发现，在 $x$ 距离 $s_i$ 较远时，会迅速减小，当距离为 $3h$ 时 $W_i(x) < 0.0002$ ，所以，应用该式时只需要考虑以 $x$ 为中心 $3h$ 为半径的邻域。
- $I(x) = 0$ 的解近似于要估计的目标曲面。

5.2 利用 IMLS 求解 $R$ 和 $t$

从 IMLS-SLAM 的角度，假设现在有一个点 $p$ ，要估计它相邻两个时刻的 $R$ 和 $t$ ，则利用 IMLS 就能很好地解决这个问题：
1. 设 $p_i \in P_k$ ， $P_k$ 是对应到 map 中，以 $p$ 为球心，半径为 $3h$ 的领域内的点。
2. 得到隐函数（可以理解为点到面的距离的变形表示）
  
  $I^{P_k}(p) = \frac{\sum_{p_i \in P_k} W_i(p) ((p - p_i) \cdot n_i)}{\sum_{p_i \in P_k} W_i(p)}$
  
  其中 $n_i$ 是 $p_i$ 的法向量，求法向量的方法即为之前的 SRI 求导法。此隐函数表示的是点 $p$ 到需要对齐的 map 中的曲面上的点 $p_i$ 距离平方的加权平均。
3. 然后，求得每一个变换后的点到曲面的距离，并令这个距离最小：
  
  $\operatorname{argmin} \sum_{x_i \in P_k} |I^{P_k}(R x_i + t)|$
  
  此处则存在一个问题， $I(x)$ 隐函数里有指数函数（ $W_i(x)$ 函数），这个非线性项不允许做线性最小二乘，因此不能直接使用 ICP 点到面的对齐方式优化求解 $R$ 和 $t$ 。

5.3 IMLS-SLAM 提出的求解方法

首先，把点投影到 IMLS 曲面上，投影结果为 $q_i$ （类比向量到平面的投影）：

$q_i = p_i - I^{P_k}(p_i) \tilde{n}_i$

其中， $\tilde{n}_i$ 是 $p_i$ 最近邻点 $p_c$ 的法线。

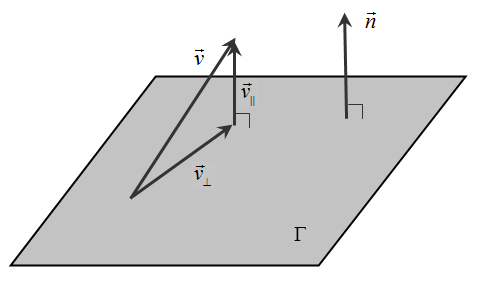图-5 向量到平面的投影
经过变换后的点，应该要落在平面上，因此有：

$\operatorname{argmin} \sum_{p_i \in P_k} |\tilde{n}_i \cdot (R p_i + t - q_i)|^2$
如下图为 ICP 和 IMLS 的对比。蓝点是来自先前 $n$ 次扫描的带有噪声的点云 $P_k$ ，红点是新扫描的点。
- 第一行显示了 ICP 点到面匹配的第一次和最后一次迭代的示例：在每次迭代中，最小化到最近点的距离。
- 第二行显示了第一次和最后一次迭代 IMLS 点到模型的距离示例：黑色虚线是 IMLS 表面，在每次迭代中，最小化到 IMLS 表面的距离之和。
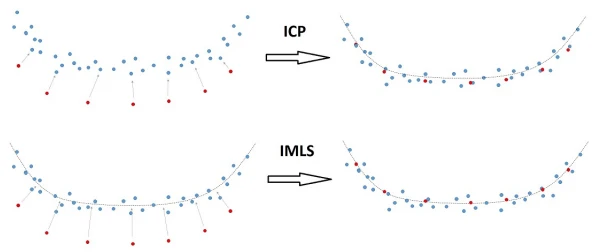图-6 ICP 和 IMLS 对比

5.4 IMLS 的基本思想

选择具有代表性的激光点来进行匹配，既能减少计算量同时又能减少激光点分布不均匀导致的计算结果出现偏移。
点云中隐藏着真实的曲面，最好的做法就是能从参考帧点云中把曲面重建出来。
曲面重建的越准确，对真实世界描述越准确，匹配的精度就越高。