对论文 Lvio-Fusion: A Self-adaptive Multi-sensor Fusion SLAM Framework Using Actor-critic Method (IROS, 2021) 的阅读整理。
Lvio-Fusion
标题:Lvio-Fusion: A Self-adaptive Multi-sensor Fusion SLAM Framework Using Actor-critic Method
作者:Yupeng Jia,Haiyong Luo,Fang Zhao,Guanlin Jiang,Yuhang Li,Jiaquan Yan,Zhuqing Jiang,Zitian Wang
会议:IROS 2021
源码:https://github.com/jypjypjypjyp/lvio_fusion
基于视觉或基于 LiDAR 的 SLAM 方法的缺点:
基于视觉的方法中,单眼相机(monocular camera)或立体相机(stereo camera)的敏感性对初始化、算法过程以及测距等带来不稳定性;
LiDAR 产生的稀疏信息使得深入发掘语义信息变得困难。
LiDAR 和相机会产生累积漂移误差,并且不使用大场景下。
文章提出了一种紧耦合的多传感器融合框架 Lvio-Fusion,其融合了立体相机、LiDAR、IMU 和 GPS。系统从 VIO 中提取关键帧,并基于关键帧结合其他传感器优化因子图。IMU 的运动估计用于视觉惯导和激光点云畸变的估计。在全局位姿图优化阶段,将运动轨迹根据机器人旋转产生的累积误差,分为多个分段,每个分段独立优化。之后,文章还讨论了当系统运行时,不同环境下不同置信度的问题。
文章主要贡献:
提出了传感器紧耦合的 SLAM 框架 Lvio-Fusion,实现高精确、实时的移动机器人运动轨迹估计。
为城市交通环境提出了一个分段的全局优化方法,以限制累积漂移误差。
提出了一个使用评价器(actor-critic)的自适应算法,用于调整不同情境下传感器的权重。
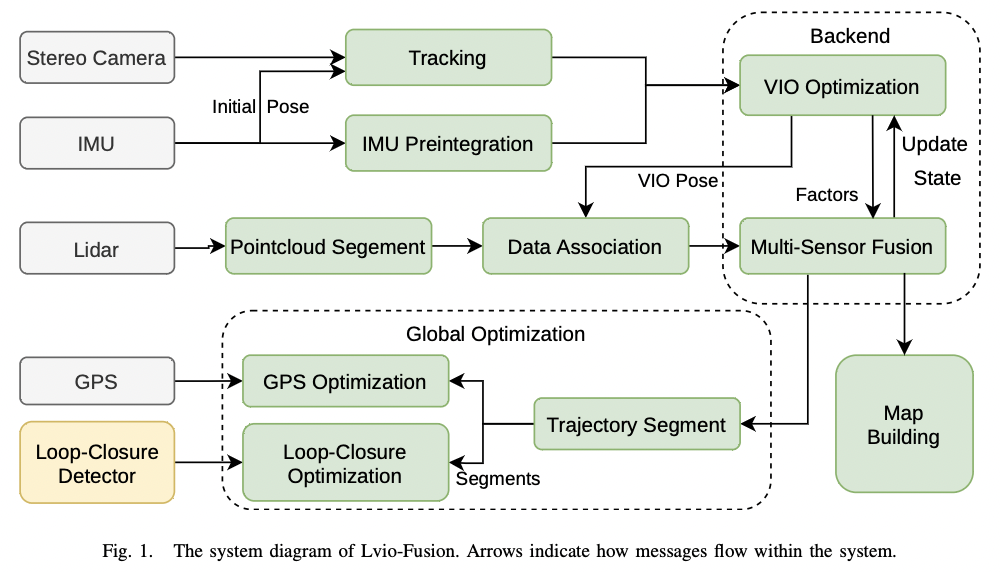
图-1 Lvio-Fusion 框架
定义世界坐标系为 W W W B B B
X = [ R T , p T , v T , b T ] T \mathcal{X} = [\pmb{R}^T, \pmb{p}^T, \pmb{v}^T, \pmb{b}^T]^T
X = [ R R R T , p p p T , v v v T , b b b T ] T
其中 R ∈ S O ( 3 ) \pmb{R} \in SO(3) R R R ∈ S O ( 3 ) p ∈ R 3 \pmb{p} \in \mathbb{R}^3 p p p ∈ R 3 v \pmb{v} v v v b \pmb{b} b b b
设计一个最大后验问题(MAP)来结合 X \mathcal{X} X X \mathcal{X} X
argmin X i ∑ i ∈ B w b i ∣ ∣ r B i ∣ ∣ 2 + ∑ ( i , j ) ∈ C w c i ρ ( ∣ ∣ r C i , j ∣ ∣ 2 ) + ∑ ( i , l ) ∈ L w l i ρ ( ∣ ∣ r L i , l ∣ ∣ 2 ) \underset{\mathcal{X}_i}{\operatorname{argmin}} \sum_{i \in \mathcal{B}} w_{b_i} ||\pmb{r}_{\mathcal{B_i}}||^2 + \sum_{(i,j) \in \mathcal{C}} w_{c_i} \rho(||\pmb{r}_{\mathcal{C_{i,j}}}||^2) + \sum_{(i,l) \in \mathcal{L}} w_{l_i} \rho(||\pmb{r}_{\mathcal{L_{i,l}}}||^2)
X i a r g m i n i ∈ B ∑ w b i ∣ ∣ r r r B i ∣ ∣ 2 + ( i , j ) ∈ C ∑ w c i ρ ( ∣ ∣ r r r C i , j ∣ ∣ 2 ) + ( i , l ) ∈ L ∑ w l i ρ ( ∣ ∣ r r r L i , l ∣ ∣ 2 )
其中 r B i , r C i , j , r L i , l \pmb{r}_{\mathcal{B_i}}, \pmb{r}_{\mathcal{C_{i,j}}}, \pmb{r}_{\mathcal{L_{i,l}}} r r r B i , r r r C i , j , r r r L i , l ρ ( ⋅ ) \rho(\cdot) ρ ( ⋅ ) w b i , w c i , w l i w_{b_i}, w_{c_i}, w_{l_i} w b i , w c i , w l i
如图-1 为系统概览图:
视觉前端立体相机获取 3D 数据,执行 frame-to-frame 的追踪。
同时,IMU 数据为 frame-to-frame 追踪和 IMU 预积分阶段提供初始位姿。
然后系统执行 VIO 第一次局部优化。
对于 LiDAR,系统提取以视觉 keyframe 为中心的点云 scan 并分割地面点云。
然后使用 VIO 的初始位姿,系统使用特征关联方法来执行第二次局部优化,此次优化包含了 LiDAR、视觉和 IMU 数据。
另外,系统也适用 GPS 约束和回环检测来优化全局位姿图。
使用 KLT 稀疏光流算法(KLT sparse optical flow)和基于特征的方法进行视觉前端的追踪。KLT 算法快速但不稳定,即使有 IMU 数据的修正也可能轻易丢失追踪。
因此,使用滑动窗口在 keyframe 中使用 feature points 构建一个 local map。当被追踪的 feature points 的数量小于阈值时,这些点对应的帧则被标记为 keyframe,并用于检测 ORB 特征点。然后这些在左、右相机中得到匹配的特征会被投影到真实 3D 空间得到 3D 坐标。
当每一个 keyframe 到来时,系统将在 local map 中搜寻 feature points,以使用描述子匹配新的特征点。
考虑第 i i i j j j
r C i , j = u j − K exp ( ξ i ∧ ) P j \pmb{r}_{\mathcal{C}_{i,j}} = \pmb{u}_j - \pmb{K} \exp (\xi_i^\wedge) \pmb{P}_j
r r r C i , j = u u u j − K K K exp ( ξ i ∧ ) P P P j
u j \pmb{u}_j u u u j K \pmb{K} K K K P j \pmb{P}_j P P P j W W W ξ i ∈ s e ( 3 ) \xi_i \in \mathfrak{se}(3) ξ i ∈ s e ( 3 )
IMU 的原始角速度和加速度为:
ω ^ t = ω t + b t ω + n t ω a ^ t = R t B W ( a t − g ) + b t a + n t a \hat{\omega}_t = \omega_t + \pmb{b}_t^\omega + \pmb{n}_t^\omega \\
\hat{\pmb{a}}_t = \pmb{R}_t^{BW} (\pmb{a}_t - \pmb{g}) + \pmb{b}_t^a + \pmb{n}_t^a
ω ^ t = ω t + b b b t ω + n n n t ω a a a ^ t = R R R t B W ( a a a t − g g g ) + b b b t a + n n n t a
ω ^ t \hat{\omega}^t ω ^ t a ^ t \hat{\pmb{a}}_t a a a ^ t B B B t t t b t \pmb{b}_t b b b t n t \pmb{n}_t n n n t R t B W \pmb{R}_t^{BW} R R R t B W W W W B B B g \pmb{g} g g g W W W
IMU 预积分用于获取 keyframe 间的相对位姿,第 i i i
r B i = [ r v i r p i r R i r b a i r b g i ] = [ R i − 1 T ( v i − v i − 1 − g Δ t i ) − Δ v ^ i R i − 1 T ( p i − p i − 1 − v i − 1 Δ t i − 1 2 g Δ t i 2 ) − Δ p ^ i R i − 1 T R i ( R ^ i − 1 i ) T b a i − b a i − 1 b g i − b g i − 1 ] \pmb{r}_{\mathcal{B}_i} =
\left[
\begin{matrix}
\pmb{r}_{\pmb{v}_i} \\
\pmb{r}_{\pmb{p}_i} \\
\pmb{r}_{\pmb{R}_i} \\
\pmb{r}_{\pmb{b}_{a_i}} \\
\pmb{r}_{\pmb{b}_{g_i}}
\end{matrix}
\right]
=
\left[
\begin{matrix}
\pmb{R}_{i-1}^T (\pmb{v}_i - \pmb{v}_{i-1} - \pmb{g} \Delta t_i) - \Delta \hat{\pmb{v}}_i \\
\pmb{R}_{i-1}^T (\pmb{p}_i - \pmb{p}_{i-1} - \pmb{v}_{i-1} \Delta t_i - {1 \over 2} \pmb{g} \Delta t_i^2) - \Delta \hat{\pmb{p}}_i \\
\pmb{R}_{i-1}^T \pmb{R}_i (\hat{\pmb{R}}_{i-1}^i)^T \\
\pmb{b}_{a_i} - \pmb{b}_{a_{i-1}} \\
\pmb{b}_{g_i} - \pmb{b}_{g_{i-1}}
\end{matrix}
\right]
r r r B i = ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ r r r v v v i r r r p p p i r r r R R R i r r r b b b a i r r r b b b g i ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ = ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ R R R i − 1 T ( v v v i − v v v i − 1 − g g g Δ t i ) − Δ v v v ^ i R R R i − 1 T ( p p p i − p p p i − 1 − v v v i − 1 Δ t i − 2 1 g g g Δ t i 2 ) − Δ p p p ^ i R R R i − 1 T R R R i ( R R R ^ i − 1 i ) T b b b a i − b b b a i − 1 b b b g i − b b b g i − 1 ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤
其中 [ Δ v ^ i , Δ p ^ i , Δ R ^ i − 1 i ] T [\Delta \hat{\pmb{v}}_i, \Delta \hat{\pmb{p}}_i, \Delta \hat{\pmb{R}}_{i-1}^i]^T [ Δ v v v ^ i , Δ p p p ^ i , Δ R R R ^ i − 1 i ] T
对于 IMU 预积分因子,初始的速度、偏差和重力方向是需要已知的,因此 IMU 初始化非常重要。当系统处于开始阶段或 IMU 被中断时,将要执行 IMU 初始化。在 IMU 初始化过程,系统选择最近的 10 个 keyframe 作为一个窗口,执行三个步骤:
窗口中加速度的平均值作为重力加速度的初始值;
仅使用 IMU 预积分因子进行优化,得到速度差和重力差的估计值;
使用视觉因子进行完整的 VIO 优化。
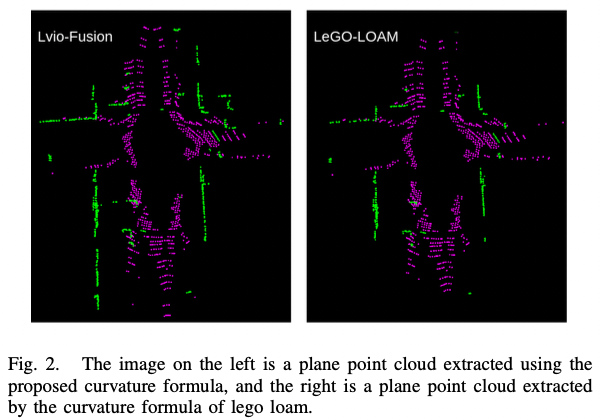
当新的 LiDAR scan 到来时,先通过相邻点极速哪曲率提取 planar feature。曲率小的点分类为 plane feature。使用下式来计算曲率:
Δ r = r i − n − r i + n 2 n c = a ( 2 n − 1 ) r i ∑ k = 1 2 n − 1 ( r i − n + k − r i − n − k Δ r ) 2 \Delta r = {r_{i-n} - r_{i+n} \over 2n} \\
c = {a \over (2n-1) r_i} \sum_{k=1}^{2n-1} (r_{i-n+k} - r_{i-n} - k \Delta r)^2
Δ r = 2 n r i − n − r i + n c = ( 2 n − 1 ) r i a k = 1 ∑ 2 n − 1 ( r i − n + k − r i − n − k Δ r ) 2
r i r_i r i a a a n n n
图-2 plane feature 的提取结果
使用 SAC(Sample Consensus)平面分割来限制 plane feature 的异常(outlier)。然后,系统结合最新的 3 个 scan 构建 local map。第 i i i l l l
r L i , l = ∣ ( p i , j − p l , u ) ⋅ ( p l , u − p l , v ) × ( p i , j − p l , w ) ∣ ∣ ( p l , u − p l , v ) × ( p i , j − p l , w ) ∣ \pmb{r}_{\mathcal{L}_{i,l}} = {|(\pmb{p}_{i,j} - \pmb{p}_{l,u}) \cdot (\pmb{p}_{l,u} - \pmb{p}_{l,v}) \times (\pmb{p}_{i,j} - \pmb{p}_{l,w})| \over |(\pmb{p}_{l,u} - \pmb{p}_{l,v}) \times (\pmb{p}_{i,j} - \pmb{p}_{l,w})|}
r r r L i , l = ∣ ( p p p l , u − p p p l , v ) × ( p p p i , j − p p p l , w ) ∣ ∣ ( p p p i , j − p p p l , u ) ⋅ ( p p p l , u − p p p l , v ) × ( p p p i , j − p p p l , w ) ∣
其中 j , u , v , w j,u,v,w j , u , v , w
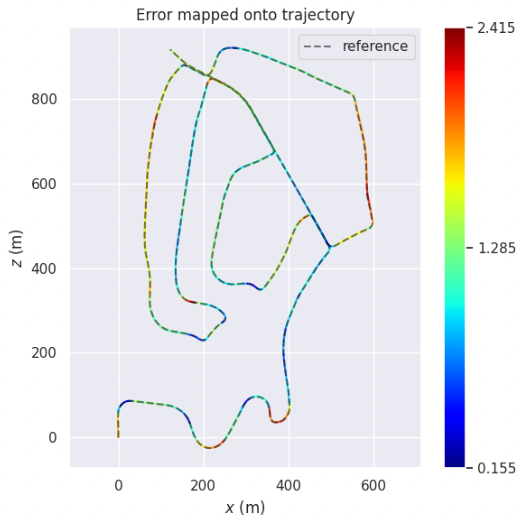
累积误差无法避免,尤其是旋转的轻微误差会导致误差不断放大累积,因此使用 GPS 和回环检测来约束全局位姿图优化。
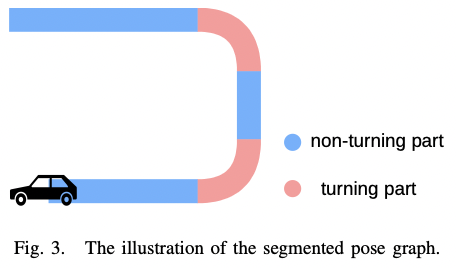
现实场景的实验中发现,车辆转弯时位姿估计的旋转误差远大于非转弯部分。将运动轨迹根据转向角分割为多个部分,如图-3,然后逐段优化位姿图。
图-3 轨迹按转向角分段
在分段位姿图优化中,有两个阶段:
使用 GPS 和回环对分段进行优化;
在相同分段的 keyframe 将根据其是否在旋转分段或非旋转分段来进行优化:旋转分段 keyframe 的旋转误差将被重点优化,而非旋转分段 keyframe 的方向误差将被重点优化。
使用强化学习来设计一个自适应的因子图优化方法。因为使用不同类型的因子进行位姿估计对反向传播来说很困难,而深度强化学习能通过策略梯度法(polivy gradient algorithm)更新参数。
标准强化学习中,agent 和 environment 通过 perception 和 action 相连。每一步交互过程,agent 以当前 environment 的状态获取 observation 作为输入,然后 agent 选择一个 action 来生成输出,从而改变 enviroment 的状态。这种状态转换的收益通过 reward 传给 agent。而 agent 也应该选择那些能长期为 reward 产生收益的 action。
基于上述框架,environment 为基于多传感器优化的因子图,action 为不同因子的权重,observation 为机器人从当前状态获取到的传感器数据,而 reward 为预测位姿与实际位姿的 RPE(relative pose error)的倒数:
r e w a r d i = ∣ ∣ ( R i − 1 R i + Δ ) − 1 ( p i − 1 p i + Δ ) ∣ ∣ − 1 reward_i = ||(\pmb{R}_i^{-1} \pmb{R}_{i + \Delta})^{-1} (\pmb{p}_i^{-1} \pmb{p}_{i + \Delta})||^{-1}
r e w a r d i = ∣ ∣ ( R R R i − 1 R R R i + Δ ) − 1 ( p p p i − 1 p p p i + Δ ) ∣ ∣ − 1
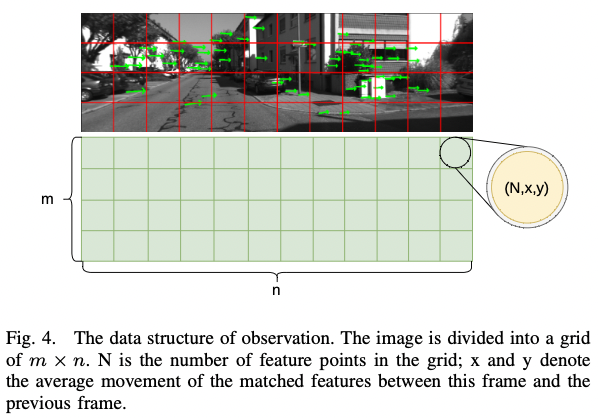
为提高准确性和实时性,使用结合特征追踪信息的矩阵作为观测值而非原始图像,如图-4:
图-4 观测值的数据结构
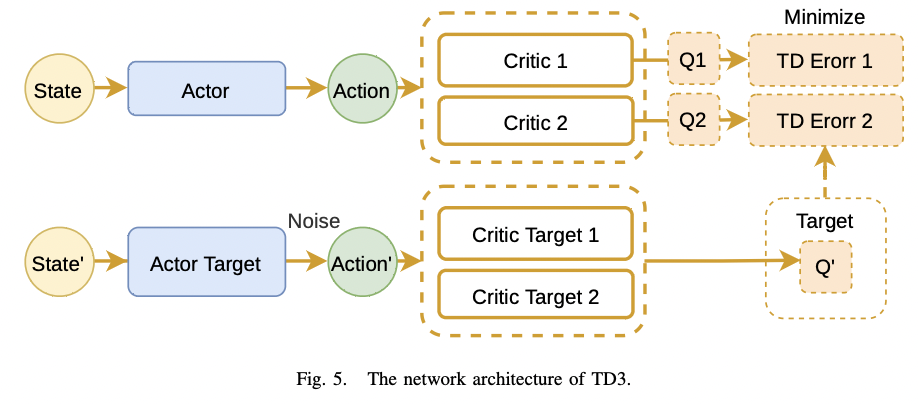
这个矩阵包含移动信息和环境信息。本文提出的网络以观测矩阵为输入,视觉因子和 LiDAR 因子的权重作为输出。使用 TD3(Twin Delayed Deep Deterministic policy gradient algorithm)来最大化长期 reward,设置 6 层的 MLP 为 backbone,TD3 框架如图-5 所示:
图-5 TD3 框架
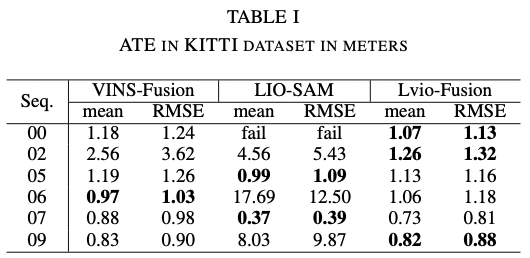
KITTI Dataset
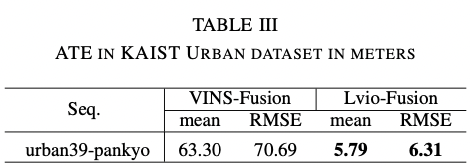
KAIST Urban Dataset
L δ ( y , f ( x ) ) = { 1 2 ( y − f ( x ) ) 2 , f o r ∣ y − f ( x ) ∣ ≤ δ δ ∣ y − f ( x ) ∣ − 1 2 δ 2 , o t h e r w i s e L_{\delta} (y, f(x)) =
\begin{cases}
{1 \over 2} (y - f(x))^2, &\mathrm{for}\ |y-f(x)| \le \delta \\
\delta |y-f(x)| - {1 \over 2} \delta^2, &\mathrm{otherwise}
\end{cases}
L δ ( y , f ( x ) ) = { 2 1 ( y − f ( x ) ) 2 , δ ∣ y − f ( x ) ∣ − 2 1 δ 2 , f o r ∣ y − f ( x ) ∣ ≤ δ o t h e r w i s e
其中 δ \delta δ
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 #include <pcl/point_types.h> #include <pcl/io/pcd_io.h> #include <pcl/filters/extract_indices.h> #include <pcl/segmentation/sac_segmentation.h> #include <pcl/visualization/cloud_viewer.h> int main (int argc, char ** argv) pcl::PCDReader reader; pcl::PointCloud<pcl::PointXYZ>::Ptr cloud (new pcl::PointCloud<pcl::PointXYZ>) ; pcl::PointCloud<pcl::PointXYZ>::Ptr cloud_plane (new pcl::PointCloud<pcl::PointXYZ>) ; reader.read ("test.pcd" , *cloud); pcl::PointIndices::Ptr inliers (new pcl::PointIndices) ; pcl::SACSegmentation<pcl::PointXYZ> seg; pcl::ModelCoefficients::Ptr coefficients (new pcl::ModelCoefficients) ; seg.setOptimizeCoefficients (true ); seg.setModelType (pcl::SACMODEL_PLANE); seg.setMethodType (pcl::SAC_RANSAC); seg.setMaxIterations (100 ); seg.setDistanceThreshold (0.15 ); seg.setInputCloud (cloud); seg.segment (*inliers, *coefficients); if (inliers->indices.size () == 0 ) { std::cout << "Could not estimate a planar model for the given dataset." << std::endl; } pcl::ExtractIndices<pcl::PointXYZ> extract; extract.setInputCloud (cloud); extract.setIndices (inliers); extract.setNegative (false ); extract.filter (*cloud_plane); std::cout << "PointCloud representing the planar component: " << cloud_plane->size () << " data points." << std::endl; pcl::visualization::PCLVisualizer viewer ("Cloud Viewer" ) ; int v1 (0 ) viewer.createViewPort (0 , 0 , 0.5 , 1.0 , v1); viewer.setBackgroundColor (0 , 0 , 0 , v1); viewer.addText ("Cloud Original" , 2 , 2 , "Cloud Original" , v1); pcl::visualization::PointCloudColorHandlerGenericField<pcl::PointXYZ> rgb1 (cloud, "z" ) ; viewer.addPointCloud <pcl::PointXYZ>(cloud, rgb1, "original cloud" , v1); viewer.setPointCloudRenderingProperties (pcl::visualization::PCL_VISUALIZER_POINT_SIZE, 1 , "original cloud" , v1); viewer.addCoordinateSystem (1.0 , "original cloud" , v1); int v2 (1 ) viewer.createViewPort (0.5 , 0 , 1.0 , 1.0 , v2); viewer.setBackgroundColor (0 , 0 , 0 , v2); viewer.addText ("Cloud Segmentation" , 2 , 2 , "Cloud Segmentation" , v2); pcl::visualization::PointCloudColorHandlerGenericField<pcl::PointXYZ> rgb2 (cloud_plane, "z" ) ; viewer.addPointCloud <pcl::PointXYZ>(cloud_plane, rgb2, "plane cloud" , v2); viewer.setPointCloudRenderingProperties (pcl::visualization::PCL_VISUALIZER_POINT_SIZE, 1 , "plane cloud" , v2); viewer.addCoordinateSystem (1.0 , "plane cloud" , v2); viewer.spin (); return (0 ); }
[1] F. Dellaert and M. Kaess, “Factor graphs for robot perception,” Found. Trends Robotics , vol. 6, no. 1-2, pp. 1–139, 2017. [Online]. Available: https://doi.org/10.1561/2300000043