Mobile3DRecon

Posted on Edited on In Waline:

对论文 Mobile3DRecon:Real-time Monocular 3D Reconstruction on a Mobile Phone (TVCG, 2020) 的阅读整理。

Mobile3DRecon
# 论文情况 - 标题：Mobile3DRecon:Real-time Monocular 3D Reconstruction on a Mobile Phone - 作者：Xingbin Yang, Liyang Zhou, Hanqing Jiang, and etc. - 会议：IEEE TRANSACTIONS ON VISUALIZATION AND COMPUTER GRAPHICS (TVCG) 2020 - 源码：（未开源，官方网站）https://zju3dv.github.io/mobile3drecon.github.io/

1 Introduction

现有的一些基于 6DoF 惯导系统的手机 AR 技术如 VINS-Mobile 主要关注于不考虑场景中深度几何结构的 sparse mapping，而深度几何结构对于场景的全面 3D 感知是关键的，并且对于更加真实的 AR（遮挡、阴影、碰撞）是十分重要的。KinectFusion、BundleFusion 等尝试使用 dense mapping 来执行 6DoF 惯导，但依赖于通过 RGB-D 相机拍摄的带深度信息的视频作为输入，同时 dense mapping 需要大量的运算，这对于大多数中低档手机来说要求过高。
为使 AR 技术能更适用于中档手机平台，本文提出了一个面向中档手机的深度表面重建系统 Mobile3DRecon。系统可以实现以单目相机实时表面网格重建（surface mesh reconstruction），无需额外的硬件或深度传感器。
主要贡献：

  • 提出了一个多视觉关键帧深度估计的方法，甚至可以在结构不清晰的区域估计稠密的深度信息。通过基于置信度的过滤方法提出 SGM（semi-global matching）来可靠地估计深度和移除因位姿错误或结构不清晰而导致的不可靠深度信息。
  • 提出了一个增强的网格生成方法，融合了计算得到的关键帧深度图来在线重建场景表面网格。
  • 提出了一个使用单目相机的实时稠密表面网格（dense surface mesh）重建方法。在中档手机的实验上，所提出的方法后端处理速度不超过 125 ms/keyframe，足够匹配前端 6DoF 追踪醉倒 25 FPS 的速度。

2 System Overview

图-1 系统框架

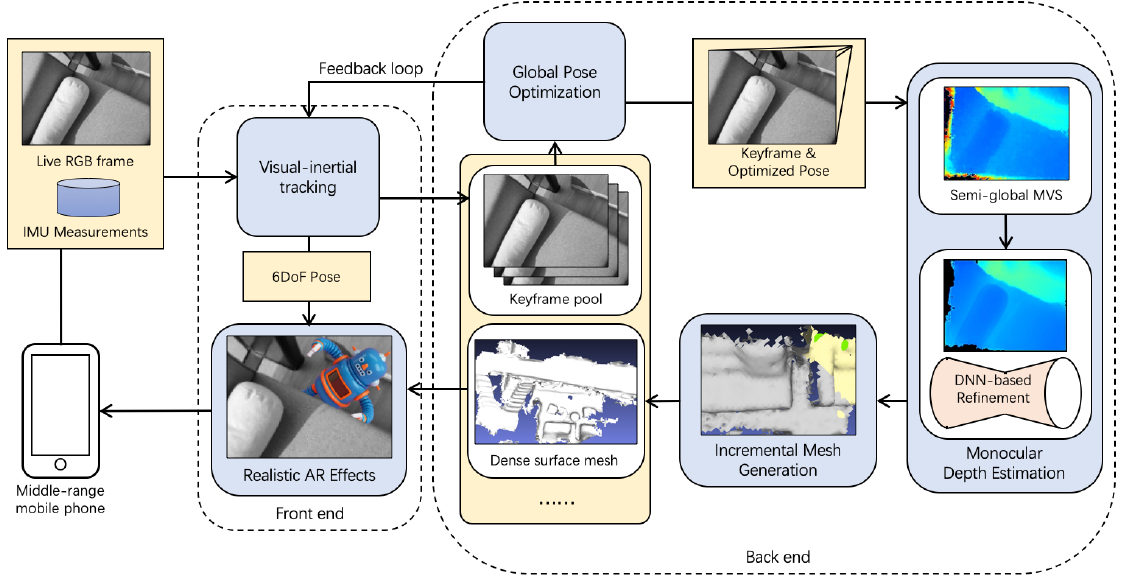
当用户使用手机单目相机进入环境当中，系统使用 SenseAR SLAM[1] 来进行位姿追踪（可以使用 AR Core)。

当前端 6DoF 的追踪初始化完成后，对于新到来的 keyframe 以及其全局优化后的位姿，其深度图通过多视觉 SGM 在线估计得到。在 SGM 后面是一个 CNN 来过滤处理深度噪声（depth noise）。经过处理后的 keyframe depth map 将被融合生成稠密表面网格。

如上图，back end 的处理包括了全局位姿优化、SGM、CNN 以及表面网格生成等。

3 Monocular Depth Estimation

使用从 SenseAR SLAM 平台获取到的全局优化 keyframe 位姿，可以实现在线估计每一个新到来 keyframe 的深度图。

本文的系统通过广义的多视觉 SGM 算法来解决多视觉深度估计问题，不同于广义的二视觉 SGM 算法[2, 3]，本文的 SGM 方法更加鲁棒，因为深度噪声可以通过多视觉损失的方式来减小。

此外，由于直接在深度空间（depth space）而不是视差空间（disparity space）计算损失，所以不需要提前进行立体校正。

同时，考虑到位姿错误、结构不清晰或者碰撞等问题导致的深度信息错误，使用基于 DNN 的优化方法来过滤和优化深度噪声。

3.1 Reference Keyframe Selection

对于每一个到来的 keyframe，寻找一些邻居 keyframe 集合作为参考帧（reference frame），用于立体多视觉算法：

  • 首先，参考帧应该为稳定的深度估计提供提供足够的视差。因为对于 baseline 较小的情况下，一个小的图像域像素匹配误差会导致深度空间的较大波动。
  • 其次，为实现全场景的重建，当前的 keyframe 应该与参考帧有足够大的重叠部分（overlap）。

为满足上述需求，选取远离当前 keyframe 的邻居 keyframe，同时避免过大的 baseline 使得重叠部分太少。为简洁，使用 tt 表示 tt 时刻的 keyframe，使用如下的式子来表示 keyframe tt 和另一个 keyframe t′t' 的 baseline 分数：

wb(t,t′)=exp⁡(−(b(t,t′)−bm)2δ2)(1)w_b(t, t') = \exp (-{(b(t, t') - b_m)^2 \over \delta^2}) \tag{1}

其中 b(t,t′)b(t, t') 为 tt 和 t′t' 之间的 baseline，bmb_m 为期望，δ\delta 为标准差，实验中设置为 bm=0.6, δ=0.2b_m = 0.6,\ \delta = 0.2。

为了更好地匹配，tt 和 t′t' 之间应该有尽可能满足相同视觉感知的区域。本文通过计算两个 keyframe 视轴（optical axis）的角度，然后大体上，大角度说明有着不同的视觉感知区域。为保证大的 overlap，定义 tt 和 t′t' 之间的视觉分数：

wv(t,t′)=max⁡(αmα(t,t′),1)(2)w_v(t, t') = \max ({\alpha_m \over \alpha(t, t')}, 1) \tag{2}

其中 α(t,t′)\alpha(t, t') 为 tt 和 t′t' 之间的视觉方向的夹角，αm\alpha_m 为阈值并设置为 10°10 \degree。

打分函数则简单地将上述两式相乘：

S(t,t′)=wb(t,t′)∗wv(t,t′)(3)S(t, t') = w_b(t, t') * w_v(t, t') \tag{3}

对于每一个新的 keyframe，在历史 keyframes 中寻找其参考帧。这些历史 keyframes 通过上述打分函数进行打分并排序，分数高的几帧将作为参考帧。

较多的关键帧有助于确保深度估计的准确性，但是将降低立体匹配计算的速度，尤其对于手机。因此，仅选择排序后前 2 个 keyframe 为参考帧。对于新的 keyframe tt，其最终分数（final score）为：

S(t)=∑t′∈N(t)S(t,t′)(4)S(t) = \sum_{t' \in N(t)} S(t, t') \tag{4}

其中 N(t)N(t) 为 tt 的参考帧集合。这个最终分数将被用于之后损失计算中的权重。

3.2 Multi-View Stereo Matching

对于每个新 keyframe，使用基于多视觉立体算法的 SGM 来计算其深度图。将逆深度空间均匀采样为 LL 个 level。假设深度测量界限于 dmind_{min} 和 dmaxd_{max} 之间，则第 ll 级采样深度为：

dl=(L−1)dmindmax(L−1−l)dmin+l(dmax−dmin), l∈{0,1,...,L−1}(5)d_l = {(L - 1) d_{min} d_{max} \over (L - 1 - l) d_{min} + l (d_{max} - d_{min})},\ l \in \{ 0, 1, ..., L-1 \} \tag{5}

给定一个 keyframe tt 中深度为 dld_l 的像素 x\pmb{x}，其投影到 keyframe t′t' 在深度 dld_l 下对应的像素 xt→t′(dl)\pmb{x}_{t \rightarrow t'}(d_l) 可以通过下式计算：

xt→t′(dl)∼dlKt′Rt′RtTKt−1x^+Kt′(Tt′−Rt′RtTTt)(6)\begin{aligned} \pmb{x}_{t \rightarrow t'} (d_l) &\sim d_l \pmb{K}_{t'} \pmb{R}_{t'} \pmb{R}_t^T \pmb{K}_t^{-1} \hat{\pmb{x}} + \pmb{K}_{t'} (\pmb{T}_{t'} - \pmb{R}_{t'} \pmb{R}_t^T \pmb{T}_t) \end{aligned} \tag{6}

其中 Kt′,Kt\pmb{K}_{t'}, \pmb{K}_{t} 为相机内参矩阵，Rt′,Rt\pmb{R}_{t'}, \pmb{R}_{t} 为旋转矩阵，Tt′,Tt\pmb{T}_{t'}, \pmb{T}_{t} 为位移矩阵（向量），x^\hat{\pmb{x}} 为 x\pmb{x} 的齐次坐标。

使用 Census Transform 的变体来计算局部图片的相似度。相比其他图片相似度计算方法（如 Normalized Cross Correlation），CT 具有边界保持的特点，同时 CT 的二进制计算有益于移动应用。本文将匹配损失定义为如下：

C(x,l)=∑t′∈N(t)wt′CT(x,xt→t′(dl))wt′=S(t′)∑τ∈N(t)S(τ)(7)C(\pmb{x}, l) = \sum_{t' \in N(t)} w_{t'} CT(\pmb{x}, \pmb{x}_{t \rightarrow t'}(d_l)) \\ w_{t'} = {S(t') \over \sum_{\tau \in N(t)} S(\tau)} \tag{7}

wt′w_{t'} 为参考帧 t′t' 的损失权重，S(t′)S(t') 为 t′t' 的 final score，CT(x,xt→t′(dl))CT(\pmb{x}, \pmb{x}_{t \rightarrow t'}(d_l)) 为两个以 x\pmb{x} 和 xt→t′(dl)\pmb{x}_{t \rightarrow t'}(d_l) 为中心的局部图片的 Census 损失。（提前设立 look-up-table 来加快 CT 过程中汉明距离的计算）

遍历每个像素计算其在 ll 层的匹配损失，得到一个大小为 W×H×LW \times H \times L 的损失矩阵，其中 WW 和 HH 为 keyframe 的宽和高。然后损失矩阵通过 Winner-Take-All 策略进行聚合获得初始 depth map。

尽管位姿误差可以在多视觉匹配过程中被稀释，但仍然存在歧义匹配的问题（区域不清晰等），将对 depth map 带来噪声。本文增加了一个额外的正则化方法惩罚像素的深度标签（采样 level）变化。特别地，对采样等级标签为 ll 的像素 x\pmb{x}，损失融合通过在邻居方向中递归的进行损失计算得到：

C^r(x,l)=C(x,l)+min⁡(C^r(x−r,l),C^r(x−r,l−1)+P1,C^r(x−r,l+1)+P1,min⁡iC^r(x−r,i)+P2)−min⁡kC^r(x−r,k)(8)\hat{C}_r(\pmb{x}, l) = C(\pmb{x}, l) + \min \left( \begin{matrix} \hat{C}_r(\pmb{x} - r, l), \\ \hat{C}_r(\pmb{x} - r, l - 1) + P_1, \\ \hat{C}_r(\pmb{x} - r, l + 1) + P_1, \\ \underset{i}{\min} \hat{C}_r(\pmb{x} - r, i) + P_2 \end{matrix} \right) - \min_k \hat{C}_r(\pmb{x} - r, k) \tag{8}

其中 C^r(x,l)\hat{C}_r(\pmb{x}, l) 为标签 ll 的像素 x\pmb{x} 在邻居方向 r∈Nrr \in N_r 下的聚合损失，邻居方向设置为 8 个方向。P1P_1 和 P2P_2 为惩罚值，其中 P2=−a∗∣∇It(x)∣+bP_2 = -a * |\nabla I_t(\pmb{x})| + b，∇It(x)\nabla I_t(\pmb{x}) 为 keyframe tt 对应图像 ItI_t 的强度梯度。min⁡kC^r(x−r,k)\min_k \hat{C}_r(\pmb{x} - r, k) 用于避免聚合损失的无限增长。图像中每个像素的最终损失为：

C^(x,l)=∑r∈NrC^r(x,l)(9)\hat{C}(\pmb{x}, l) = \sum_{r \in N_r} \hat{C}_r (\pmb{x}, l) \tag{9}

最终的深度 level 标签则通过 Winner-Take-All 策略得到：

l^(x)=argmin⁡lC^(x,l)(注：原文中为 l^(x)=min⁡lC^(x,l)，感觉不符合此处对 l^(x) 的描述)(10)\hat{l} (\pmb{x}) = \underset{l}{\operatorname{argmin}} \hat{C} (\pmb{x}, l) \\ (注：原文中为\ \hat{l} (\pmb{x}) = \underset{l}{\operatorname{min}} \hat{C} (\pmb{x}, l)，感觉不符合此处对\ \hat{l} (\pmb{x})\ 的描述) \tag{10}

为了获得 sub-level 的深度值，先使用抛物线拟合的方法进行计算：

l^s(x)=l^(x)+C^(x,l^(x)−1)−C^(x,l^(x)+1)2C^(x,l^(x)−1)−4C^(x,l^(x))+2C^(x,l^(x)+1)(11)\hat{l}_s(\pmb{x}) = \hat{l}(\pmb{x}) + {\hat{C}(\pmb{x}, \hat{l}{(\pmb{x}) - 1}) - \hat{C}(\pmb{x}, \hat{l}{(\pmb{x}) + 1}) \over 2 \hat{C}(\pmb{x}, \hat{l}{(\pmb{x})-1}) - 4\hat{C}(\pmb{x}, \hat{l}{(\pmb{x})}) + 2\hat{C}(\pmb{x}, \hat{l}(\pmb{x})+1)} \tag{11}

用 l^s(x)\hat{l}_s(\pmb{x}) 替换上述式子 (5) 中的 ll 得到 x\pmb{x} 的 sub-level 深度。有了 sub-level 深度，可以得到一个初始的 keyframe tt 的深度图 DtiD_t^i，如图-4(b)。

实验中使用 NEON 技术来加速损失的计算和融合。

3.3 Depth Refinement

尽管文中的方法已经比 SLAM 更加鲁棒，但是仍然存在深度噪声。

3.3.1 Confidence-Based Depth Filtering

尽管上述 SGM 方法获得的 depth map 已经很完整，但是在某些结构不清晰的区域仍然明显存在噪声，因此需要置信度测量来深化深度信息的过滤。在 Drory 等人的方法[4] 中，提出了为 SGM 方法计算像素 x\pmb{x} 的不确定性的方法：

U(x)=min⁡l∑r∈NrC^r(x,l)−∑r∈Nrmin⁡l(C^r(x,l)−Nr−1NrC(x,l))(12)U(\pmb{x}) = \min_l \sum_{r \in N_r} \hat{C}_r(\pmb{x}, l) - \sum_{r \in N_r} \min_l (\hat{C}_r (\pmb{x}, l) - {N_r - 1 \over N_r} C(\pmb{x}, l)) \tag{12}

然而这种方法忽略了邻居的深度信息，造成了某些离散的深度噪声，如图-2 (d)。

图-2 深度信息过滤

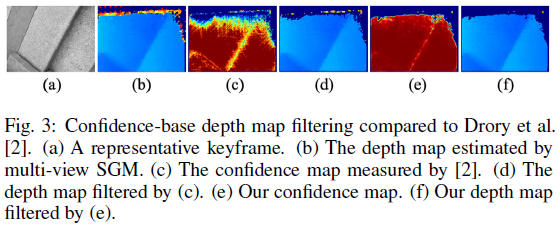
考虑到正确的深度测量结果下，邻居像素的深度不会大幅度改变，因此为 x\pmb{x} 在其周围 5×55\times5 的窗口 Ω(x)\Omega(\pmb{x}) 内计算一个权重 ω(x)\omega(\pmb{x})，测量其邻居的深度 level 的不同：

ω(x)=1∣Ω(x)∣∑y∈Ω(x)[∣l^s(x)−l^s(y)∣>2](13)\omega (\pmb{x}) = {1 \over |\Omega(\pmb{x})|} \sum_{\pmb{y} \in \Omega(\pmb{x})} [|\hat{l}_s(\pmb{x}) - \hat{l}_s(\pmb{y})| > 2] \tag{13}

标准化加权的不确定性得到最终的置信度 M(x)M(\pmb{x})：

M(x)=1−ω(x)U(x)max⁡u∈It(ω(u)U(u))(14)M(\pmb{x}) = 1 - {\omega(\pmb{x}) U(\pmb{x}) \over \underset{\pmb{u} \in I_t}{\max} (\omega(\pmb{u}) U(\pmb{u}))} \tag{14}

在实验中，将置信度低于 0.150.15 的像素移除，得到过滤后的深度图 DtfD_t^f，这样就使得大多数的 outliers 被移除，但还是会留下小部分的噪声，如图-4 ©。

3.3.2 DNN-Based Depth Refinement

在经过基于置信度的深度融合后，使用一个 DNN 来进一步过滤深度噪声。

图-3 DNN 框架

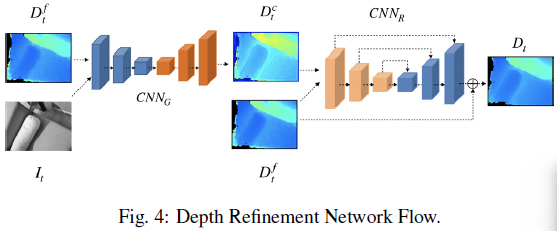
这里的 DNN 可以是为 two-stage 的结构：

  • 第一阶段：CNNGCNN_G 结合 keyframe tt 的过滤后深度图 DtfD_t^f 和对应的灰度图 ItI_t 得到一个粗糙的 refinement 结果 DtcD_t^c。此处 ItI_t 作为一个引导者来引导深度 refinement，其提供了对象边缘和语义信息的先验知识。
  • 第二阶段：残差 U-Net CNNRCNN_R 进一步优化 DtcD_t^c 得到最终的深度图 DtD_t。U-Net 的主要用于是学习过程更加稳定。

引入三种空间损失函数[5, 6, 7] 来惩罚深度噪声同时保留边缘信息，训练的损失函数定义为：

Φ=Φedge+Φpd+λΦvgg(15)\Phi = \Phi_{edge} + \Phi_{pd} + \lambda \Phi_{vgg} \tag{15}

Φedge\Phi_{edge} 为边缘维护损失，包含三个组成部分（Φx\Phi_x 和 Φy\Phi_y 计算的是沿着边缘的深度差异，Φn\Phi_n 为法向量的相似度）：

Φedge=Φx+Φy+ΦnΦx=1∣It∣∑x∈Itln⁡(∣∇xDt(x)−∇xDtg(x)∣+1)Φy=1∣It∣∑x∈Itln⁡(∣∇yDt(x)−∇yDtg(x)∣+1)Φn=1∣It∣∑x∈It(1−ηt(x)∗ηtg(x))(16)\Phi_{edge} = \Phi_x + \Phi_y + \Phi_n \\ \begin{aligned} \Phi_x &= {1 \over |I_t|} \sum_{\pmb{x} \in I_t} \ln (|\nabla_x D_t(\pmb{x}) - \nabla_x D_t^g(\pmb{x})| + 1) \\ \Phi_y &= {1 \over |I_t|} \sum_{\pmb{x} \in I_t} \ln (|\nabla_y D_t(\pmb{x}) - \nabla_y D_t^g(\pmb{x})| + 1) \\ \Phi_n &= {1 \over |I_t|} \sum_{\pmb{x} \in I_t} (1 - \eta_t (\pmb{x}) * \eta_t^g (\pmb{x})) \end{aligned} \tag{16}

此处 ∣It∣|I_t| 为 ItI_t 中还保留着的像素点数，Dtg(x)D_t^g(\pmb{x}) 表示像素 x\pmb{x} 的 ground truth 深度值。∇x\nabla_x 和 ∇y\nabla_y 代表沿 x 轴和 y 轴的 Sobel 导数。深度法向量 ηt(x)\eta_t(\pmb{x}) 近似为 ηt(x)=[−∇xDt(x),∇yDt(x),1]\eta_t (\pmb{x}) = [- \nabla_x D_t(\pmb{x}), \nabla_y D_t(\pmb{x}), 1]，ηtg(x)\eta_t^g(\pmb{x}) 则为对应的通过相同方法计算得到的 ground truth 法向量。

Φpd\Phi_{pd} 为光度计损失（photometric loss）：

Φpd=1∣It∣∑x∈It(∣∇x2Dt(x)∣e−α∣∇xIt(x)∣+∣∇y2Dt(x)∣e−α∣∇yIt(x)∣)(17)\Phi_{pd} = {1 \over |I_t|} \sum_{\pmb{x} \in I_t} (|\nabla_x^2 D_t(\pmb{x})| e^{- \alpha |\nabla_x I_t(\pmb{x})|} + |\nabla_y^2 D_t(\pmb{x})| e^{- \alpha |\nabla_y I_t(\pmb{x})|}) \tag{17}

其中实验中取 α=0.5\alpha = 0.5，∇x2\nabla_x^2 和 ∇y2\nabla_y^2 为沿 x 轴和 y 轴的二阶导。使用二阶导的目的是让 refinement 过程更加稳定。

Φvgg\Phi_{vgg} 为 high-level perceptual loss[7]，通过最小化高阶层特征之间的差异来维护全局数据分布。

实验在 Demon 数据集上进行。首先在 Demon 数据集上经过 SGM 和基于置信度的过滤方法生成一系列初始的过滤后 depth maps，然后将其与 ground truth 融合进行预训练。然后与训练后的模型将在作者用 OPPO R17 Pro 采集的数据集上进行深度训练。

如图-4 (d) 为经过 DNN 训练和计算后得到的深度图结果。

图-4 单目相机深度测量结果

4 Incremental Mesh Generation

估计的深度将被融合仿真生成在线的 surface mesh。

TSDF（truncated signed distance function）在用于实时的网格重建。

本文中的 mesh 生成方法执行可扩展的 TSDF 体素融合，以避免体素哈希冲突，同时根据新融合体素的 TSDF 变化增量更新表 surface mesh。通过这种增量网格更新来在一个 CPU 核的情况下在手机上完成实时网格扩展。

4.1 Scalable Voxel Fusion

传统的 TSDF 虽然简洁，但是计算复杂并且消耗内存，不利于手机上实时的大场景重建。体素哈希被证明由于其低内存消耗和动态体素分配的方式，对于大型场景的重建是更具扩展性的，但仍然需要解决由哈希函数带来的哈希冲突问题。

受这些的启发，本文提出了结合传统 TSDF 体素索引和体素哈希优点的可扩展哈希算法。

4.1.1 Scalable Hash Function

图-5 TSDF Cube

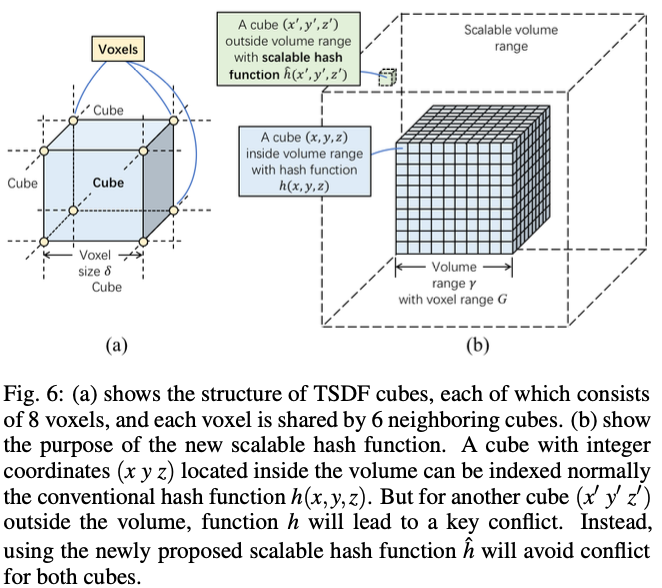
如图-5 (a) 为 TSDF 算法所提取出的 cube 和体素。在本文提出的算法中，每一个 cube 及其相关的体素都能被分配一个唯一的编码。

假设有一个 3D 容器，预定义的大小为 γ\gamma，每一维的范围为 [−γ/2,γ/2)[-\gamma / 2, \gamma / 2)。G=γ/δG = \gamma / \delta 为每一维的体素数量，其中 δ\delta 为体素的大小（如 0.06m0.06 \mathrm{m}）。对于 volume 中的一个 3D 点 V=(fx,fy,fz)\pmb{V} = (fx, fy, fz)，其所属的 cube 可以由以下的哈希函数索引到：

h(x,y,z)=g(x)+g(y)∗G+g(z)∗G2(x,y,z)=(⌊fxδ⌋,⌊fyδ⌋,⌊fzδ⌋)(18)h(x, y, z) = g(x) + g(y) * G + g(z) * G^2 \\ (x, y, z) = (\lfloor {fx \over \delta} \rfloor, \lfloor {fy \over \delta} \rfloor, \lfloor {fz \over \delta} \rfloor) \tag{18}

其中：

g(i)=i+G2, i∈[−G2,G2)g:[−G2,G2)↦[0,G)g(i) = i + {G \over 2},\ i \in [-{G \over 2}, {G \over 2}) \\ g: [-{G \over 2}, {G \over 2}) \mapsto [0, G)

式子 (18) 可以将一个 volume 内的 3D 点分配到一个唯一索引，然而当一个 3D 点不在 volume 内时，如图-5 (b)，将出现冲突：

  • 假设 G=5G = 5，点 Va\pmb{V}_a 在 volume 中有坐标 (g(x),g(y),g(z))=(1,1,0)(g(x), g(y), g(z)) = (1, 1, 0)，此时得到哈希值 66；若点 Vb\pmb{V}_b 在 volume 中计算得到的坐标为 (6,0,0)(6, 0, 0)，则也会得到同样的哈希值，从而产生冲突。

为解决上述冲突，此处重新定义哈希函数：

h^(x,y,z)=OC+g^(x)+g^(y)∗G+g^(z)∗G2g^(i)=i+GOG2(19)\hat{h}(x, y, z) = O_C + \hat{g}(x) + \hat{g}(y) * G + \hat{g}(z) * G^2 \\ \hat{g}(i) = i + {G O_G \over 2} \tag{19}

其中 OGO_G 为较大的体素维度索引的偏移，OCO_C 为全局偏移：

OG={⌊2i^G⌋+1,i^>0⌊−(2i^+1)G⌋+1,i^≤0, i^=argmax⁡i∈{x,y,z}∣i∣OC=G3∑k=1OG−1k3(20)O_G = \begin{cases} \lfloor {2 \hat{i} \over G} \rfloor + 1, &\hat{i} > 0 \\ \lfloor {- (2 \hat{i} + 1) \over G} \rfloor + 1, &\hat{i} \le 0 \end{cases} ,\ \hat{i} = \underset{i \in \{ x, y, z \}}{\operatorname{argmax}} |i| \\ O_C = G^3 \sum_{k = 1}^{O_G - 1} k^3 \tag{20}

  • 有了式子 (19)，Vb\pmb{V}_b 重新计算得到哈希值为 286286。

此处的哈希改进是将索引范围从 [0,G3)[0, G^3) 扩大到了 [0,(GOG)3)[0, (GO_G)^3)。这种改进扩大了哈希索引范围，避免了两个随机点产生的哈希冲突。

4.1.2 Voxel Fusion with Dynamic Objects Removal

假设有 tt 时刻的 depth map DtD_t，对于像素 x=(u,v)\pmb{x} = (u, v) 的深度值 d∈Dtd \in D_t，将其投影到 3D 空间得到一个 3D 点 P=Mt−1ρ(u,v,d)P = \pmb{M}_t^{-1} \rho(u, v, d)，其中 ρ(u,v,d)=(u−cufud,v−cvfvd,d)\rho(u, v, d) = ({u - c_u \over f_u} d, {v- c_v \over f_v} d, d)。(fu,fv)(f_u, f_v) 为在 u 和 v 方向点焦距长度，(cu,cv)(c_u, c_v) 为 2D 图像的中心，Mt\pmb{M}_t 为将全局 3D 空间转换到局部相机空间的转换矩阵。点 PP 所在的 cube 的哈希索引由 (19) 式得到。

如图-5，每个 cube 有 8 个关联体素，每个体素 V\pmb{V} 在第一次遍历到或者被更新时，将作为下式的新输入值：

Tt(V)=Tt−1(V)+d(MtV)−Dt(π(MtV))Wt(V)=Wt−1(V)+1(21)T_t (\pmb{V}) = T_{t-1} (\pmb{V}) + d(\pmb{M}_t \pmb{V}) - D_t (\pi (\pmb{M}_t \pmb{V})) \\ W_t (\pmb{V}) = W_{t-1} (\pmb{V}) + 1 \tag{21}

其中 π(x,y,z)=(xzfu+cu,yzfv+cv)\pi(x, y, z) = ({x \over z}f_u + c_u, {y \over z}f_v + c_v) 为投影函数，为简洁，记 π(x,y,z)=x\pi(x, y, z) = \pmb{x}；d(MtV)d(\pmb{M}_t \pmb{V}) 为 keyframe tt 下体素 V\pmb{V} 在局部相机空间的投影深度；D(x)D(\pmb{x}) 为像素 x\pmb{x} 的深度测量值；Tt(V)T_t(\pmb{V}) 和 Wt(V)W_t(\pmb{V}) 为体素 V\pmb{V} 在时间 tt 的 TSDF 值和权重。对于新生成的体素，有：

Tt(V)=d(MtV)−Dt(π(MtV))Wt(V)=1T_t (\pmb{V}) = d(\pmb{M}_t \pmb{V}) - D_t (\pi (\pmb{M}_t \pmb{V})) \\ W_t (\pmb{V}) = 1

有了 (21) 中的体素更新方法，可以实时地更新和生成被深度测量所占据的 cube 周围的体素。特别地，维护一个 cube 列表来记录所有生成的 cube。对于列表中的每一个 cube，与其相关联的体素哈希也被记录下来，使得两个相邻的 cube 可以用相同的哈希来共享体素。

使用 Marching cubes 算法从 cube 列表里提取出等值面（iso-surface）。注意到如果任何和 cube 相关联的 TSDF 体素被投影到 depth map 边界外或者投影到错误的深度像素中，则和这个 cube 相关联的所有体素的更新都需要还原。如果一个 cube 的 8 个体素在 TSDF 更新后值均小于 0，则这个 cube 需要被移除。

图-6 动态物体移除

如图-6，现实的 AR 场景重建中会遇到画面中存在动态物体的情况，尤其是画面中的物体出现后停留片刻又离开，将对场景重建带来极大的困难。

除了更新与当前估计深度测量相关联的体素外，还将每个现有体素 V\pmb{V} 投射到当前帧 tt，以进行深度可见性检查：

  • 如果 d(MtV)<Dt(x)d(\pmb{M}_t \pmb{V}) < D_t(\pmb{x})，即深度测量结果在模型的前侧，此时出现了可见性冲突。这在一个物体进入相机视觉内停留了前几帧后，而在后续几帧中又消失的情况下发生。体素融合了物体保持静止的前几帧，在之后几帧中物体消失了，这就引发了冲突。解决这种情况的方式就是深入的使用式子 (21) 更新体素 V\pmb{V} 的 TSDF 值。
  • 如果 d(MtV)≪Dt(x)d(\pmb{M}_t \pmb{V}) \ll D_t(\pmb{x})，TSDF 值将很快下降至小于 0，使得其关联的 cube 被无效化。这种策略使得被动态物体所占据的 cube 很快被移除。

使用这些策略，移动物体将被逐渐移除，重建出 surface mesh。

4.2 Incremental Mesh Updating

Marching cube 是一个从 TSDF 值中提取 iso-surface 的有效算法，被广泛用于一些深度重建系统。然而，由于频繁的插值操作导致的性能问题，这些系统大多在实时重建完成后作为后处理进行表面提取。大多数 AR 应用需要实时的网格生成来支持增量更新。本文设计了一个增量网格更新策略，仅占用 1 个 CPU 线程，避免前端对 GPU 资源的占用。

这里的增量更新策略是基于每个 keyframe 中需要被更新的 cubes，iso-surface 则从这些 cube 中生成。为得到那些参与表面提取的 cubes，设每个体素有状态变量 χ(V)∈{ADD,UPDATE,NORMAL,DELETE}\chi(\pmb{V}) \in \{ ADD, UPDATE, NORMAL, DELETE \}：

  • 如果 V\pmb{V} 为新分配的体素，则其状态设为 ADDADD；
  • 如果 V\pmb{V} 的 TSDF 值 Tt(V)T_t(\pmb{V}) 在 tt 发生更新，则状态设为 UPDATEUPDATE；
  • 如果 Tt(V)≤0T_t(\pmb{V}) \le 0 或者 Wt(V)≤0W_t(\pmb{V}) \le 0，则状态设为 DELETEDELETE，也就是说 V\pmb{V} 需要从当前的体素列表中移出，然后移入空体素列表并等待重新分配。

一个 cube 的至少一个关联体素的状态为 UPDATEUPDATE 或 ADDADD 时，定义这个 cube 为 updated。在经过 4.1.2 中的体素更新后，从 updated cube 提取网格三角（mesh triangles），如果提取的网格三角已经存在，则移除这些重复的三角。当网格三角提取完成后，这些体素的状态被设为 NORMALNORMAL。

如果一个 cube 的一个关联体素状态为 DELETEDELETE，则定义这个 cube 为 deleted，由其提取的网格三角也需要移除。

如图-7 为增量网格更新的过程：

图-7 增量网格更新

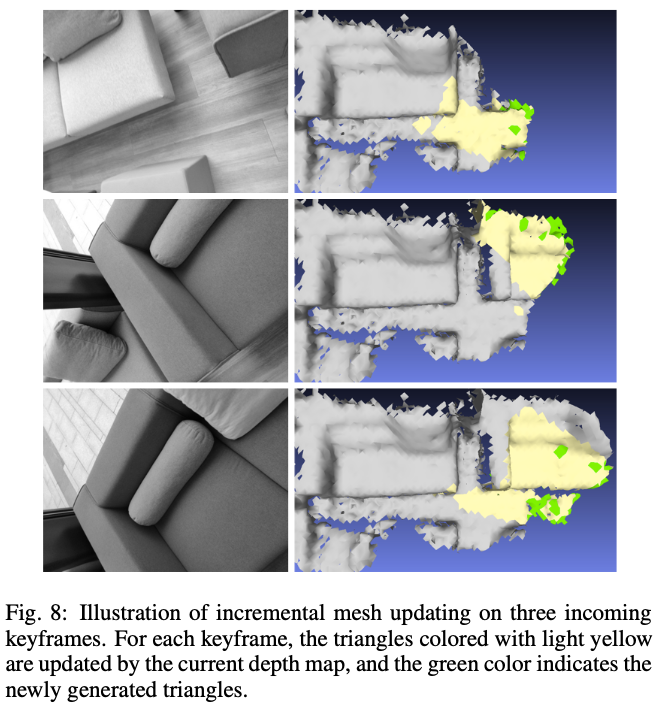
如图-8 为四种场景下表面网格重建的结果：

图-8 网格重建结果

5 Experiment

5.1 实验设置

  • 实验中使用的中档手机型号：OPPO R17 Pro
  • 实验代码及第三方库：C++，OpenCV 2，Eigen 3

5.2 定量和定性实验结果

  • depth map 重建结果对比：
图-9 深度图重建对比
图-10 深度图重建对比 2
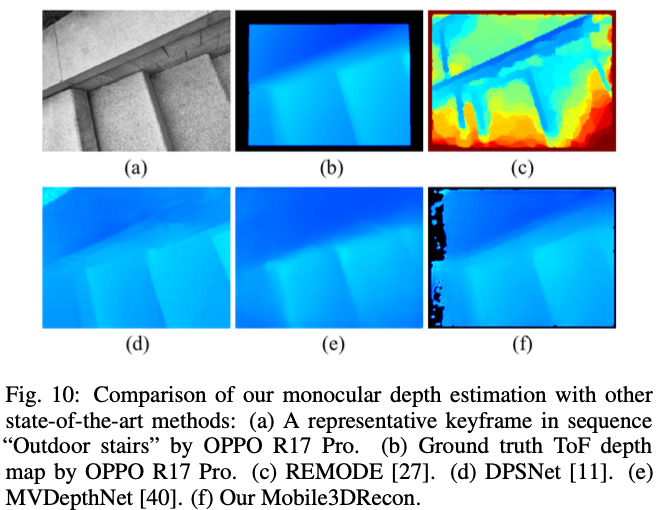
  • 实验结果的准确度：
图-11 实验结果误差
  • 处理时间：
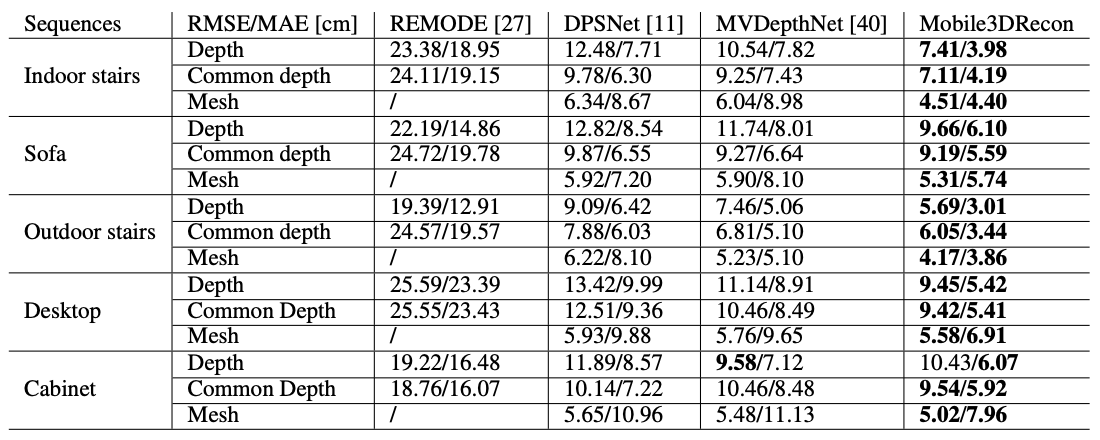
图-12 各项计算的处理时间

5.2 AR 应用

  • Unity mobile 平台上实现 AR 效果，如 occlusion 和 collision：
图-13 Unity 上的应用效果

附录

1 Census Transform（CT）

1.1 立体匹配算法

主要分为两大类：

  • 基于全局约束：在本质上属于优化算法，它是将立体匹配问题转化为寻找全局能量函数的最优化问题，其代表算法主要有图割算法、置信度传播算法和协同优化算法等。全局算法能够获得较低的总误匹配率，但算法复杂度较高，很难满足实时的需求，不利于在实际工程中使用。

  • 基于局部约束：主要是利用匹配点周围的局部信息进行计算，由于其涉及到的信息量较少，匹配时间较短，因此受到了广泛关注，代表算法主要有 SAD、SSD、NCC 等。

1.2 基于局部约束的立体匹配算法

Census Transform（CT）：在实际场景中，造成亮度差异的原因有很多，如：由于左右摄像机不同的视角接受到的光强不一致、摄像机增益、电平存在差异，以及图像采集不同通道的噪声不同等。Cencus 方法保留了窗口中像素的位置特征，并且对亮度偏差较为鲁棒，简单讲就是能够减少光照差异引起的误匹配。

实现原理：

  1. 在视图中选取任一点，以该点为中心划出一个例如 3×33 × 3 的矩形。
  2. 矩形中除中心点之外的每一点都与中心点进行比较，灰度值小于中心点则记为1，灰度大于中心点则记为0，以所得长度为 8 的只有 0 和 1 的序列作为该中心点的 census 序列，即中心像素的灰度值被 census 序列替换。
  3. 经过 CT 后的图像使用汉明距离计算相似度，图像匹配就是在视差图中找出与参考像素点相似度最高的点，而汉明距离正是视差图像素与参考像素相似度的度量。具体而言，对于欲求取视差的左右视图，要比较两个视图中两点的相似度，可将此两点的 census 值逐位进行异或运算，然后计算结果为1 的个数，记为此两点之间的汉明值。

汉明值是两点间相似度的一种体现，汉明距越小即相似度越高。

1.3 代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
using namespace cv;

void CensusTransform(Mat input_image, Mat& modified_image, int window_sizex, int window_sizey) {
    int image_height = input_image.rows;
    int image_width = input_image.cols;

    modified_image = Mat::zeros(image_height, image_width, CV_64F);

    // Census Transform
    int offsetx = (window_sizex - 1) / 2;
    int offsety = (window_sizey - 1) / 2;
    for(int j = 0; j < image_width - window_sizex; j++) {
        for(int i = 0; i < image_height - window_sizey; i++) {
            unsigned long census = 0;
            // 窗口中心像素
            uchar current_pixel = input_image.at<uchar>(i + offsety, j + offsetx); 
            // 方形窗口
            Rect roi(j, i, window_sizex, window_sizey); 
            Mat window(input_image, roi);

            for(int a = 0; a < window_sizey; a++) {
                for(int b = 0; b < window_sizex; b++)  {
                    if (!(a == offsety && b == offsetx)) {  // 中心像素不做判断
                        census = census << 1; // 左移1位
                    }
                    uchar temp_value = window.at<uchar>(a, b);
                    if (temp_value <= current_pixel ) { // 当前像素小于中心像素
                        census += 1;
                    }
                }
            }
            modified_image.at<double>(i + offsety, j + offsetx) = census;
        }
    }
}

1.4 参考

2 Winner-Take-All（胜者为王）

2.1 聚类任务

任务中没有给出每个类别的标准特征，需要考察样本间的相似情况，将相似的样本聚为一类，此外还要找到每类的标准特征，即聚类中心。

比较两个样本的相似性可转化为测量两个样本点在样本空间的距离，并以此距离的大小作为两样本相似性的度量。

虽然从 2D 和 3D 样本空间的图中可以十分清晰地看出样本间的距离远近，从而可以通过目测发现隐藏在 2D 或 3D 样本空间中的聚类，但是随着样本空间维数的增加，很难再通过目测来进行观察。

一般来说，需要用某种合适的聚类算法来解决具体问题。

2.2 最简单的聚类算法——胜者为王

该算法可以分为三个步骤：

  1. 初始化聚类中心：拟将样本聚为多少类，就需要设置多少个权向量，每个权向量代表某一类的聚类中心。聚类中心的初始化方法很多，可以用随机数为每个向量赋值，也可以随机指定某个样本。
  2. 确定竞争获胜的权向量：从训练集中随机且不重复的抽取样本为算法的输入，每个输入样本均与权向量进行相似性比较，即测量当前输入样本在样本空间的位置与各个权向量在样本空间的欧氏距离，与当前输入样本欧氏距离最短的权向量在相似性竞争中获胜。
图-附 1 获胜权向量
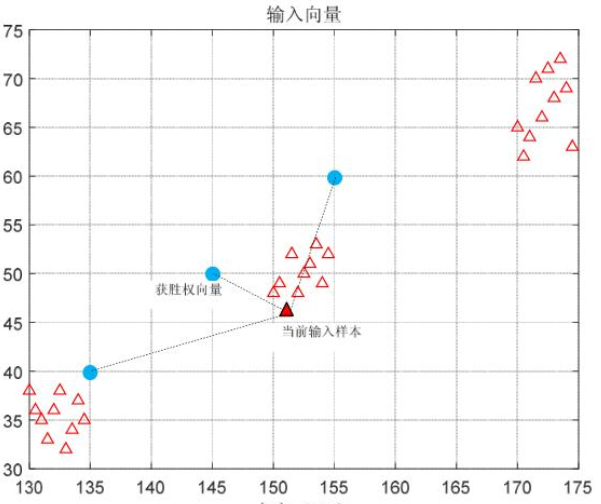
  1. 获胜权向量的权值调整：胜者为王算法规定只有获胜权向量才可进行权值调整。调整方法是：令权向量想当前输入样本方向移动一步，步长与两点间的距离成正比。比例系数 α∈(0.1]\alpha \in (0. 1] 为学习率。
图-附 2 权向量调整
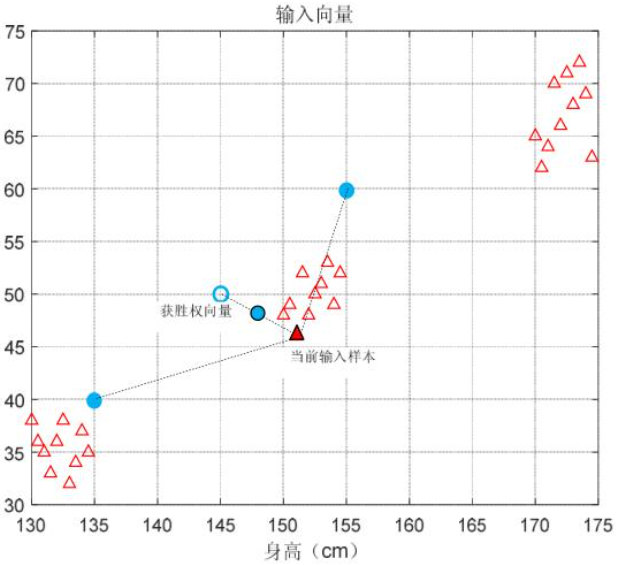
  1. 返回 2 输入下一个样本，直到训练至设定的训练次数。

2.3 参考

3 Sobel 算子

3.1 Sobel 算子

Sobel 算子：是离散微分算子（discrete differentiation operator），用来计算图像灰度的近似梯度，梯度越大越有可能是边缘。

Soble 算子的功能集合了高斯平滑和微分求导，又被称为一阶微分算子，求导算子，在水平和垂直两个方向上求导，得到的是图像在 X 方向与 Y 方向梯度图像。

缺点：比较敏感，容易受影响，要通过高斯模糊（平滑）来降噪。

3.2 计算方法

假设被作用图像为 II：

  • 水平变化：将 II 与一个基数大小的内核进行卷积。如当内核大小为 3 时，X 轴方向的梯度 GxG_x 的计算结果为：

    Gx=[−10+1−20+2−10+1]∗IG_x = \left[ \begin{matrix} -1 &0 &+1 \\ -2 &0 &+2 \\ -1 &0 &+1 \end{matrix} \right] * I

  • 竖直变化：类比水平变化。Y 轴方向的梯度 GyG_y 的计算结果为：

    Gy=[−1−2−1000+1+2+1]∗IG_y = \left[ \begin{matrix} -1 &-2 &-1 \\ 0 &0 &0 \\ +1 &+2 &+1 \end{matrix} \right] * I

在图像的每一像素上，结合两个偏导结果求出近似梯度：

G=Gx2+Gy2G = \sqrt{G_x^2 + G_y^2}

有时也写为：

G=∣Gx∣+∣Gy∣G = |G_x| + |G_y|

3.3 参考

4 TSDF（Truncated Signed Distance Function）

4.1 简介

TSDF（基于截断的带符号距离函数）算法，是一种在 3D 重建中计算 iso-surface 的方法。在拥有大内存的显卡并行计算的情况下，可以做到实时重建的效果。

4.2 算法思路

用一个大空间（volume），这个空间可以完全包括要建立的 3D 模型，volume 由许多 voxel 构成：

图-附 3 Volume

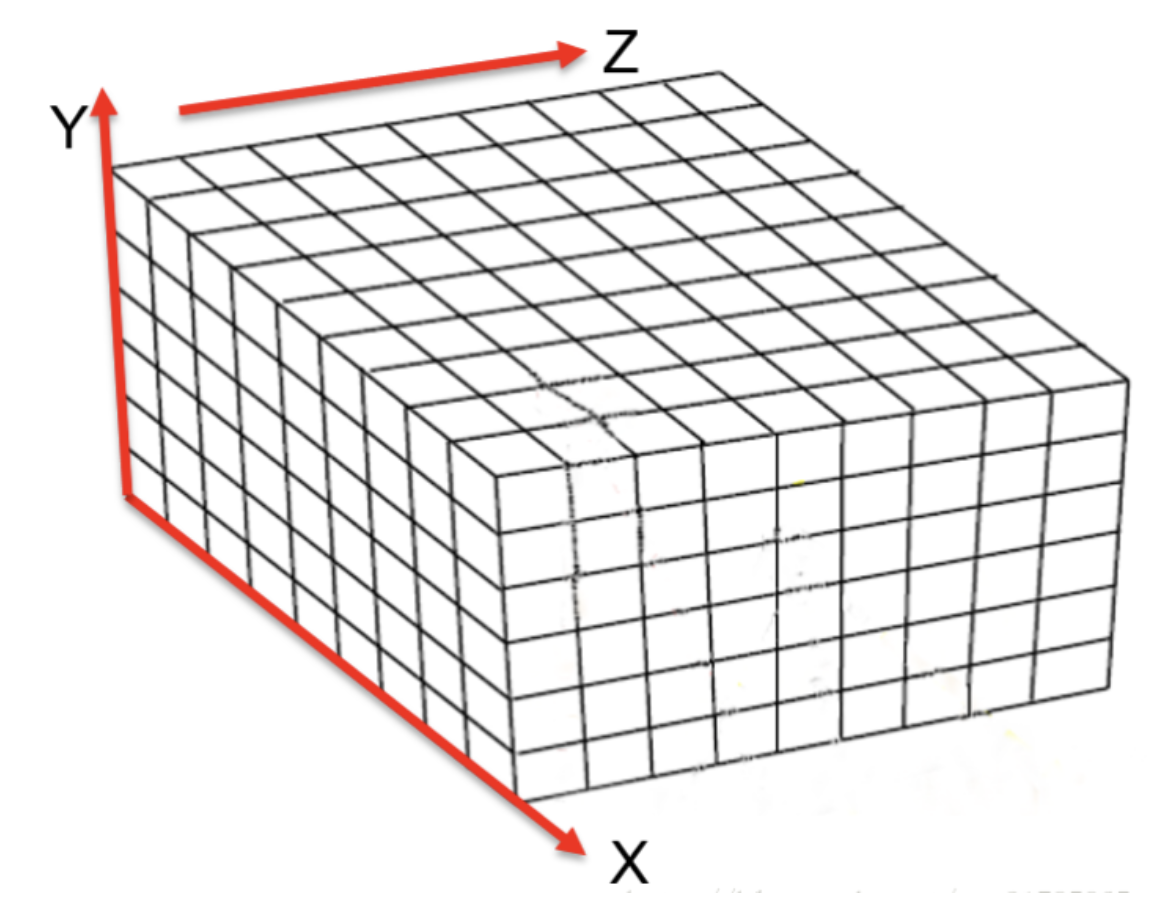
对每个 voxel（记为 VV）对应空间中的一个点，这个点用两个量来评价：

  1. 该 voxel 到最近的 surface（一开始不知道，设为没有）的距离，记为 T(V)T(V)，即带符号距离；
  2. 体素更新时的权重，记为 W(V)W(V)。
图-附 4 带符号距离

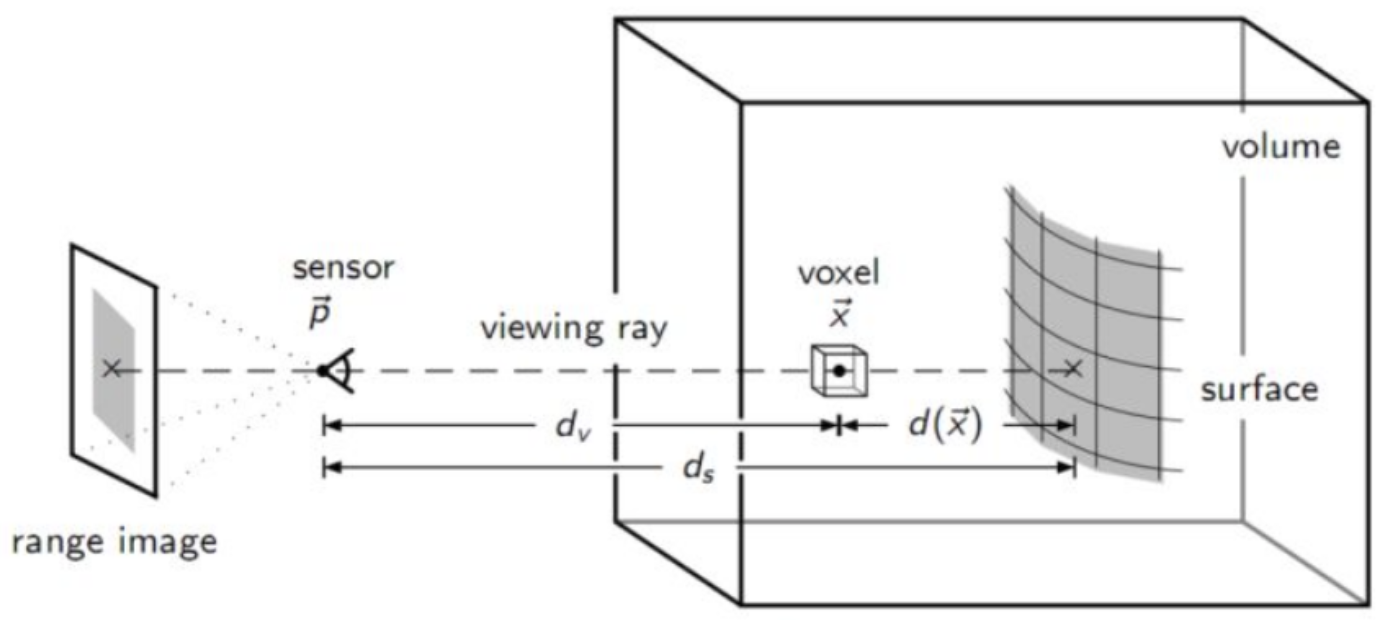
假设真实的平面到相机的深度为 dsd_s，相机采集到的深度为 dvd_v，那么符号距离就是

d(V)=ds−dvd(V) = d_s - d_v

当 d(x)>0d(x) > 0，说明体素在真实面的前面，否则在真实面后面。每次相机采集的数据都认为是最大可能的真实面，也有可能在数据的前后，但是概率要小。这个前后距离可以进行一定限制，如果距离特别远，那么概率会很小，就可以忽略。

4.3 算法步骤

  1. 准备：

    • 建立 volume，能够包围要重建的物体；
    • 划分 voxel，其大小取决于 voxel 数目和 volume 的划分；
    • 对于每个 voxel，转化其为世界坐标系下的 3D 位置点 pp。

  2. 遍历所有 voxel，计算 TSDF 值和权重：

    • 由深度数据的相机位姿矩阵，求世界坐标系下点 pp 在相机坐标系下的映射点 vv，并由内参矩阵反投影 vv 求深度图像中对应的像素点 xx，xx 的深度值记为 value(x)value(x)，点 vv 到相机坐标原点点距离为 distance(v)distance(v)；

    • pp 的 SDF 值为 sdf(p)=value(x)−distance(v)sdf(p) = value(x) - distance(v)，设截断距离为 uu，则有

      tsdf(p)=max⁡(−1,min⁡(1,sdf(P)u))tsdf(p) = \max (-1, \min(1, {sdf(P) \over u}))

    • 计算权重：

      w(p)=cos⁡θdistance(v)w(p) = {\cos \theta \over distance(v)}

      其中 θ\theta 为投影光线与 surface 法向量的夹角。

  3. 当前帧与全局融合结果进行融合。

    如果当前帧是第一帧，则第一帧为融合结果；否则需要当前帧与之前的融合结果进行再融合。以 TSDF(p)TSDF(p) 为融合 TSDF 值，W(p)W(p) 为融合权重，tsdf(p)tsdf(p) 为当前帧的 TSDF 值，w(p)w(p) 为当前帧的权重值，则更新公式如下：

    TSDFt(p)=Wt−1(p)TSDFt−1(p)+wt(p)tsdft(p)Wt−1(p)+wt(p)Wt(p)=Wt−1(p)+wt(p)TSDF_t (p) = {W_{t-1} (p) TSDF_{t-1} (p) + w_t (p) tsdf_t (p) \over W_{t-1} (p) + w_t (p)} \\ W_t (p) = W_{t-1} (p) + w_t (p)

每添加一帧深度数据，就执行一遍 2，3 步，直到最后输出结果，给 Marching Cube 计算三角面。

4.4 参考

5 Marching Cubes Algorithm

5.1 等值面（iso-surface）

等值面是空间中的一个曲面，规定空间中每一个点都有一个属性值，属性值相等的连续空间组成的曲面，称之为等值面。

在采集深度点云时，由于传感器自身精度以及配准的误差在一个地方会采集到很多点，可以认为是对空间连续点的采样，而且点的位置会有很大的波动。通过一些其他方法可以得出这些点与真正的面的差值。那么真正的面在哪？

假如一个点在面的前方，标记为 +1+1，一个点在真实面的后方，标记为 −1-1，可以认为这个真正的面就在这两个点的中间。

还可以这么认为，空间内真正的面会产生一个场，场内有无数个等值面，这个值暂且称之为空间场值，空间场值在面的前方为正值，后方为负值。离真实面越近，空间场值的绝对值越小，真实面的空间场值为 00。目的就是在对这个场进行采样后，找到空间内真正的面。

5.2 Marching Cube（MC）算法简介

MC 是 W.Lorensen 等人于 1987 年提出来的一种体素级重建方法。MC 算法也被称为“等值面提取”（Iso-surface Extraction）算法。

5.3 算法思路

Marching Cube 首先将空间分成众多的六面体 cube，类似将空间分成很多的小块。然后找到等值面经过的 cube，如下图：

图-附 5 cube 示意

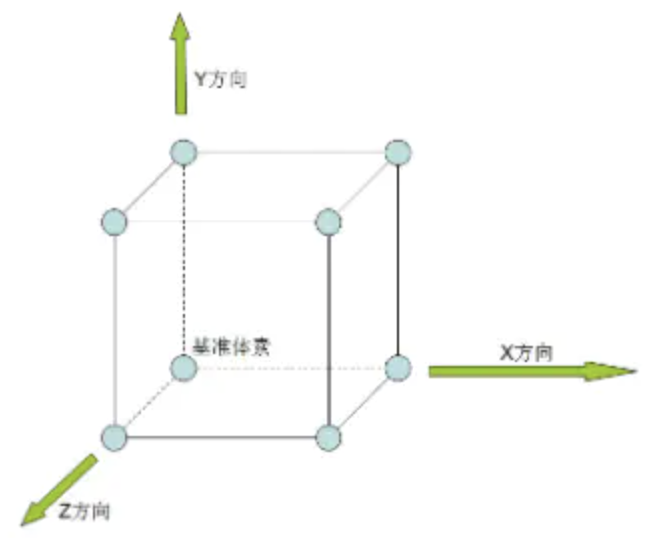
求出该 cube 的边与 0 等值面（0 等值面就是空间场值为 0 的等值面）的交点，将这些交点按照一定的拓扑连接关系连接起来，作为 0 等值面在该 cube 中的近似表示。注意是近似表示，采用三角形。

5.3.1 如何找到等值面经过的六面体网格

前面提到，有很多的已知采样点，并且知道这些点在空间中的空间场值，现在我们将空间分为很多个小格子，每个小格子都有 8 个顶点，通过计算 8 个顶点周围（范围与 cube 的大小相关）的采样点，近似计算出 8 个顶点的空间场值（加权平均等方法）。可以对 cube 做以下分类：

  • 8 个顶点都没有空间场值，0 等值面不经过或者经过但是没有采样，没有办法进行近似，所以不处理。
  • 8 个顶点都有或部分有空间场值，当空间场值都是正值或者都是负值时，说明 0 等值面不在 cube 内。
  • 当 cube 的顶点的空间场值有正有负时，则说明有 0 等直面穿过 cube。则需要从众多 cube 内，筛选出这样的 cube。

5.3.2 怎么求 cube 边与 0 等值面的交点

因为 cube 有 8 个顶点，8 个顶点的状态就有 28=2562^8 = 256 种，但是由于 cube 具有对称性，通过对称性，可以简化这些状态至 15 种状态：

图-附 6 cube 的 15 种状态

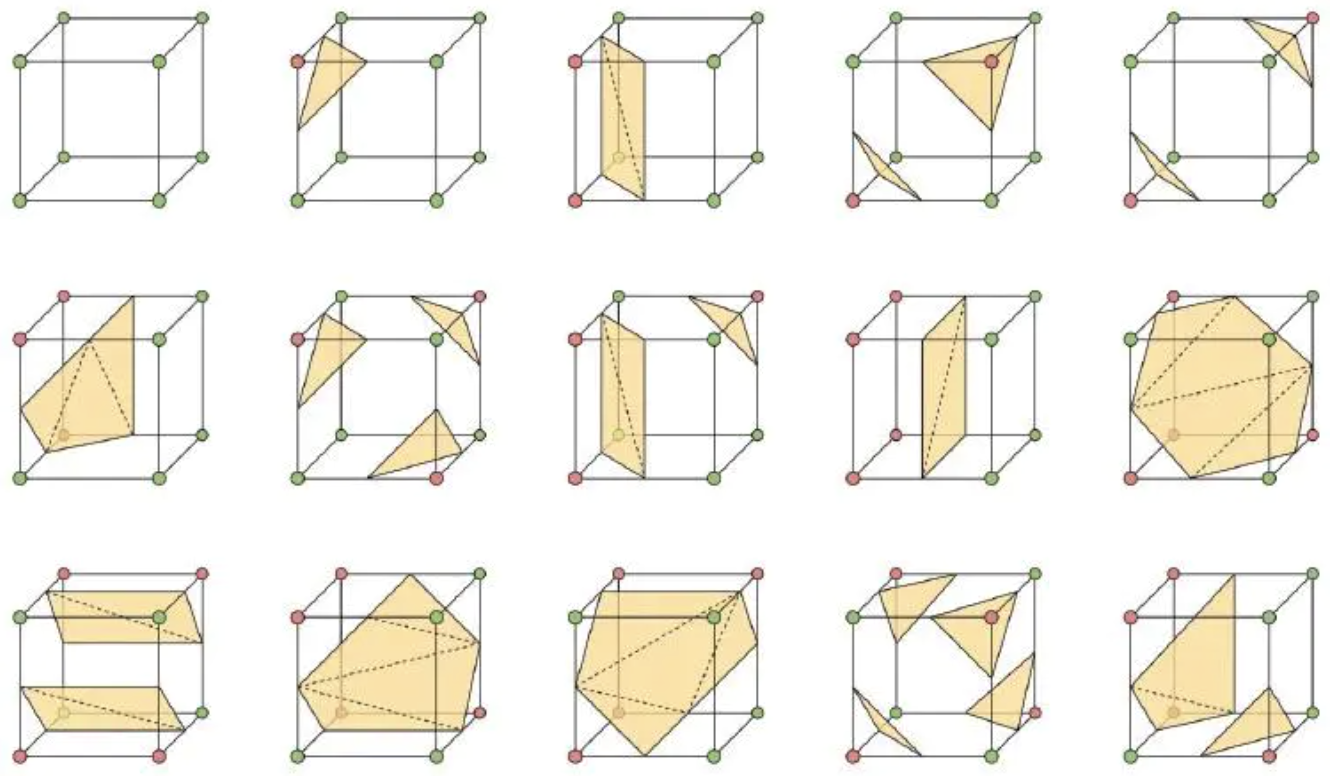
现在需要精算出来这个交点的具体的位置，举一个例子，先给 cube 的所有的顶点和边标记：

图-附 7 Marching Cube举例-1

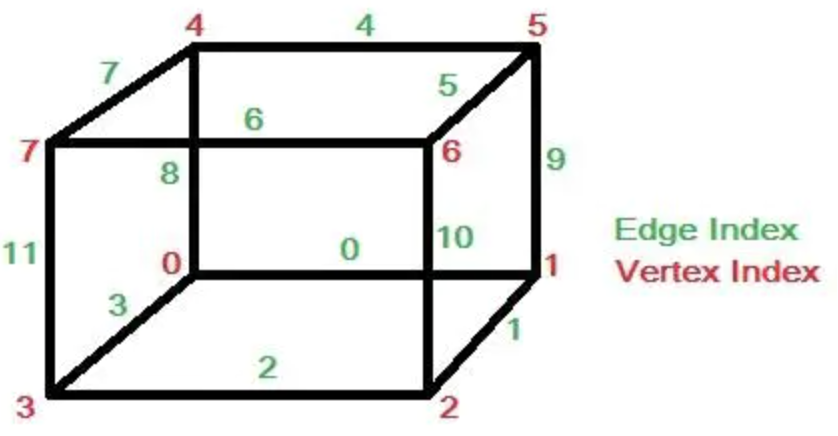
假如体素下方的顶点 3 的值小于等值面值，其他顶点上的值都大于等值面值，那么可以生成一个与体素边 2，3，11 相交的三角面片，而三角面片顶点的具体位置则需要根据等值面值和边顶点 3-2，3-0，3-7 的值线性插值计算得到。

图-附 8 Marching Cube举例-2

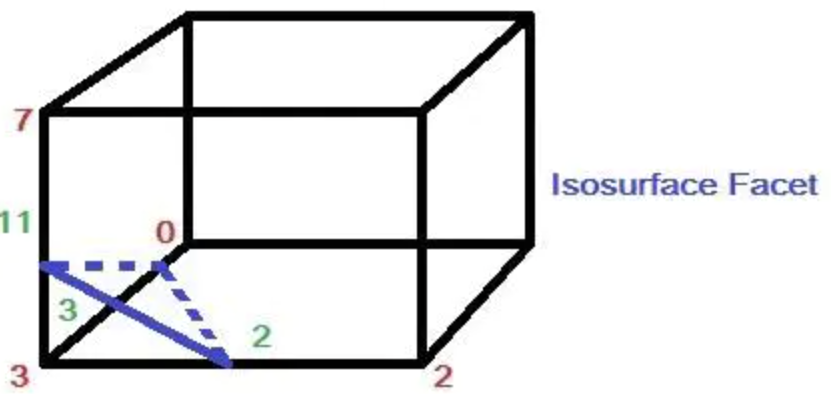
将交点坐标用 PP 表示，P1P_1、P2P_2 代表边上两个端点的坐标，V1V_1、V2V_2 代表这两个端点上的值，VV 代表等值面值，那么交点坐标的计算公式如下（线性插值，也可以是其他方法）：

P=P1+V−V1V2−V1(P2−P1)P = P_1 + {V - V_1 \over V_2 - V_1} (P_2 - P_1)

那么现在对所有的含有等值面的 cube 计算出了其与等值面的交点。最后一步，就是将这些交点连接成三角形。

5.3.3 这些交点按照怎么的拓扑连接关系连接，是怎么操作的？

连接三角形的拓扑结构，也在前面 15 中情况中，都画了出来，只要按照上图的表中已经记录好的连接关系，就可以将三角形连接出来。

5.4 算法流程

  1. 将原始数据经过预处理之后，读入特定的数组或者八叉树中。

  2. 从 volume 中提取一个 cube，成为当前 cube 同时获取该 cube 的所有信息，例如 8 个顶点的值，坐标位置等。

  3. 将当前 cube 的 8 个顶点的函数值与给定等值面值 C 进行比较,得到该 cube 的状态表。

  4. 根据当前 cube 的状态表索引，找出与等值面相交的 cube 棱边，并采用线性插值的方法计算出各个交点的位置坐标。

  5. 利用中心差分法，求出当前 cube 的 8 个顶点的法向量，采用线性插值的方法，得到三角面各个顶点的法向量。

  6. 根据各个三角面顶点的坐标、顶点法向量进行三角面的连接。

5.5 参考

参考

  • [1] http://openar.sensetime.com
  • [2] H. Hirschmuller. Accurate and efficient stereo processing by semi-global matching and mutual information. In IEEE Computer Society Conference on Computer Vision and Pattern Recognition, vol. 2, pp. 807–814, 2005.
  • [3] H. Hirschmuller. Stereo processing by semiglobal matching and mutual information. IEEE Transactions on Pattern Analysis and Machine Intelli- gence, 30(2):328–341, 2007.
  • [4] A. Drory, C. Haubold, S. Avidan, and F. A. Hamprecht. Semi-global matching: A principled derivation in terms of message passing. In German Conference on Pattern Recognition, pp. 43–53. Springer, 2014.
  • [5] C. Godard, O. Mac Aodha, and G. J. Brostow. Unsupervised monocular depth estimation with left-right consistency. In IEEE Conference on Computer Vision and Pattern Recognition, pp. 270–279, 2017.
  • [6] J. Hu, M. Ozay, Y. Zhang, and T. Okatani. Revisiting single image depth estimation: Toward higher resolution maps with accurate object bound-aries. In IEEE Winter Conference on Applications of Computer Vision, pp. 1043–1051, 2019.
  • [7] J. Johnson, A. Alahi, and L. Fei-Fei. Perceptual losses for real-time style transfer and super-resolution. In European Conferenceon Computer Vision, pp. 694–711. Springer, 2016.