Online Matching MR-SLAM

Posted on Edited on In Waline:

对论文 Multi-Robot Distributed Semantic Mapping in Unfamiliar Environments through Online Matching of Learned Representations (ICRA, 2021) 的阅读整理。

Online Matching MR-SLAM

论文情况

  • 标题：Multi-Robot Distributed Semantic Mapping in Unfamiliar Environments through Online Matching of Learned Representations
  • 作者：Stewart Jamieson, Kaveh Fathian, Kasra Khosoussi, Jonathan P. How, Yogesh Girdhar
  • 会议：ICRA, 2021
  • 源码：https://gitlab.com/warplab/ros/sunshine

1　Introduction

目标检测系统大多不支持先验的未知类。这种复杂性使得找到使用无监督学习在线开发新的语义表示的算法至关重要，以便语义映射系统可以检测和分类新的观察结果。

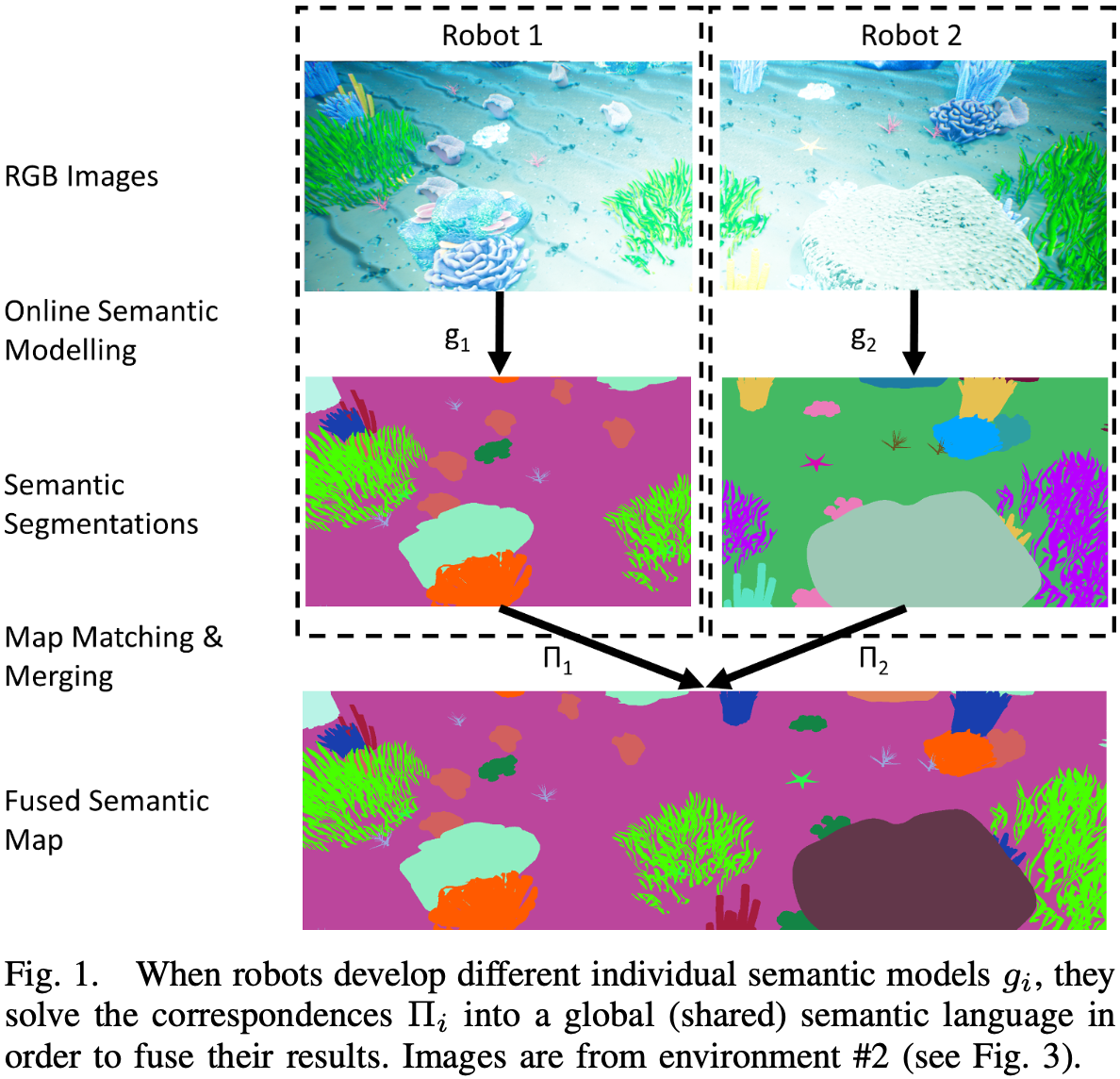
在使用无监督在线学习语义表示时，学习到的模型是自我中心的。如图-1：一个机器人学习了另一个机器人学习的相同语义标签（用颜色表示）的不同排列。除了对应标签的排列未知之外，一个机器人学习到的标签可能与另一个机器人观察到的任何标签都不对应，或者一个标签可能代表另一个机器人学习到的多个标签的并集。因此，具有学习表示的多机器人分布式语义建图需要正确估计不同标签的总数，并将对应于同一语义类别的标签进行关联和融合。

本文提出了新的多机器人分布式语义建图系统，以解决上述问题：

  • 每个机器人使用一个在线语义 3D 地图系统对自己的观察进行建模，并创建一个高质量的语义地图。
  • 机器人并行探索目标环境，在通信允许的情况下，彼此以及与人类操作员共享其学习到的语义地图和模型。
  • 在任何机器人上运行的多路匹配算法估计整个机器人团队观察到的独特现象的总数，找到被不同机器人标记不同的相同现象之间的匹配，并融合局部地图以获得所有机器人之间一致的全局地图。

2　Problem Setup

假设环境建图为 E⊂R3E \subset \mathbb{R}^3。将 EE 分为数个单元格 B={bi}\mathcal{B} = \lbrace b_i \rbrace 即 E=∪ibiE = \cup_i b_i。oracle（操作员）可以为每个格子分配语义标签 ZH\mathcal{Z}^H 的分布。假设当这些格子足够小时，每个格子可以被表示为单一标签。定义 GT 语义分割 f:B→ZHf: \mathcal{B} \rightarrow \mathcal{Z}^H，其中 f(b)∈ZHf(b) \in \mathcal{Z}^H 表示认为给 b∈Bb \in \mathcal{B} 的语义标签。模型 ff 和集合 ZH\mathcal{Z}^H 是先验未知的，因为 oracle 不知道任务期间会发现什么，而且通信带宽的限制使 oracle 无法看到大多数观测值。机器人队的目标是建立一个融合语义地图 g:B→ZGg: \mathcal{B} \rightarrow \mathcal{Z}^G，其中 ZG\mathcal{Z}^G 为学习到的语义标签的共享集合，使得 g(b)g(b) 相似于 f(b)f(b)。

假设有 NN 个机器人。在时间 tt，第 nn 个在无监督框架 gn,t:B→Ztng_{n,t}: \mathcal{B} \rightarrow \mathcal{Z}^n_t 下收集观测图像并构建了局部语义地图，Znt\mathcal{Z}_n^t 为机器人构建的语义标签观测。由于建图以自我为中心，机器人可能会构建不同的语义模型，如图-1。为构建融合的语义地图，必须首先将这 NN 个语义模型进行融合，以使用一组共同的标签。因此，机器人队必须构建全局标签集 ZtG\mathcal{Z}_t^G，以及对应的变换 Πt={Πn,t:Ztn→ZtG}n=1N\Pi_t = \lbrace \Pi_{n,t}: \mathcal{Z}_t^n \rightarrow \mathcal{Z}_t^G \rbrace_{n=1}^N。在时间 tt，给定 Πt\Pi_t，可以将单个语义地图融合到全局地图 gt:B→ZtGg_t: \mathcal{B} \rightarrow \mathcal{Z}_t^G。每个标签的计算为 gt(b)=Πnb∗,t(gnb∗,t(b))g_t(b) = \Pi_{n_b^*, t}(g_{n_b^*,t}(b))，nb∗n_b^* 为近期观测到单元格 bb 的机器人索引。

3　Consistent Online Topic Matching

3.1　Onine STM-Based Semantic Mapping

使用 BNP-ROST[1] 模型：该模型不需要预训练；可以通过改变特征词汇、单元格大小和三个标量超参数对模型进行调优，词汇表是特定于领域的，而单元格大小和标量超参数是针对特定任务进行调优的，执行同一任务的所有机器人都使用相同的超参数；最后，每个机器人的主题模型使用随机过程，根据自己的观察在线开发一组主题。

时间 tt 第 nn 个机器人有 Kn,tK_{n,t} 个主题，即 Ztn={1,…,Kn,t}\mathcal{Z}_t^n = \lbrace 1, \dots, K_{n,t} \rbrace。每个主题 zk∈Ztnz_k \in \mathcal{Z}_t^n 特征化为描述子 ϕk∈ΔV\phi_k \in \Delta^V（在 VV 个视觉词汇上的分布），其中ΔV={p∈R+V:∥p∥1=1}\Delta^V = \lbrace p \in \mathbb{R}_{+}^V: \| p \|_1 = 1 \rbrace 为。环境 EE 的每个单元格 bib_i 标记为一个极大似然主题，这个主题随着模型的引入会发生改变。

3.2　Computing Topic Similarity

需要定义一个主题相似测量来识别多个机器人是否产生了语义等价的主题。由于描述子 ϕk\phi_k 表达了概率密度函数，考虑在离散概率分布上进行相似性度量。TVD（Total Variation Distance）[2] 测量两个主题为相同词汇集合分配的概率的最大可能差异。因此，主题重叠（TO）计算如下：

TO⁡(ϕ1,ϕ2)=1−TVD⁡(ϕ1,ϕ2)(1)\operatorname{TO}(\phi_1, \phi_2) = 1 - \operatorname{TVD}(\phi_1, \phi_2) \tag{1}

TO 描述了两个描述子产生的相似度，其中 TVD⁡(ϕ1,ϕ2)=12∥ϕ1−ϕ2∥1\operatorname{TVD}(\phi_1, \phi_2) = \frac{1}{2} \| \phi_1 - \phi_2 \|_1。

另一种方式则是计算描述子的余弦相似度（CS）：

CS⁡(ϕ1,ϕ2)=ϕ1⋅ϕ2∥ϕ1∥∥ϕ2∥(2)\operatorname{CS}(\phi_1, \phi_2) = \frac{\phi_1 \cdot \phi_2}{\| \phi_1 \| \| \phi_2 \|} \tag{2}

上述两种计算是对称且界定在 [0,1][0,1] 内的，值越大说明主题相似度越大。使用度量方法构建逐对相似图，一个加权无向图，顶点为主题，边的权重为相似度，如图-2。

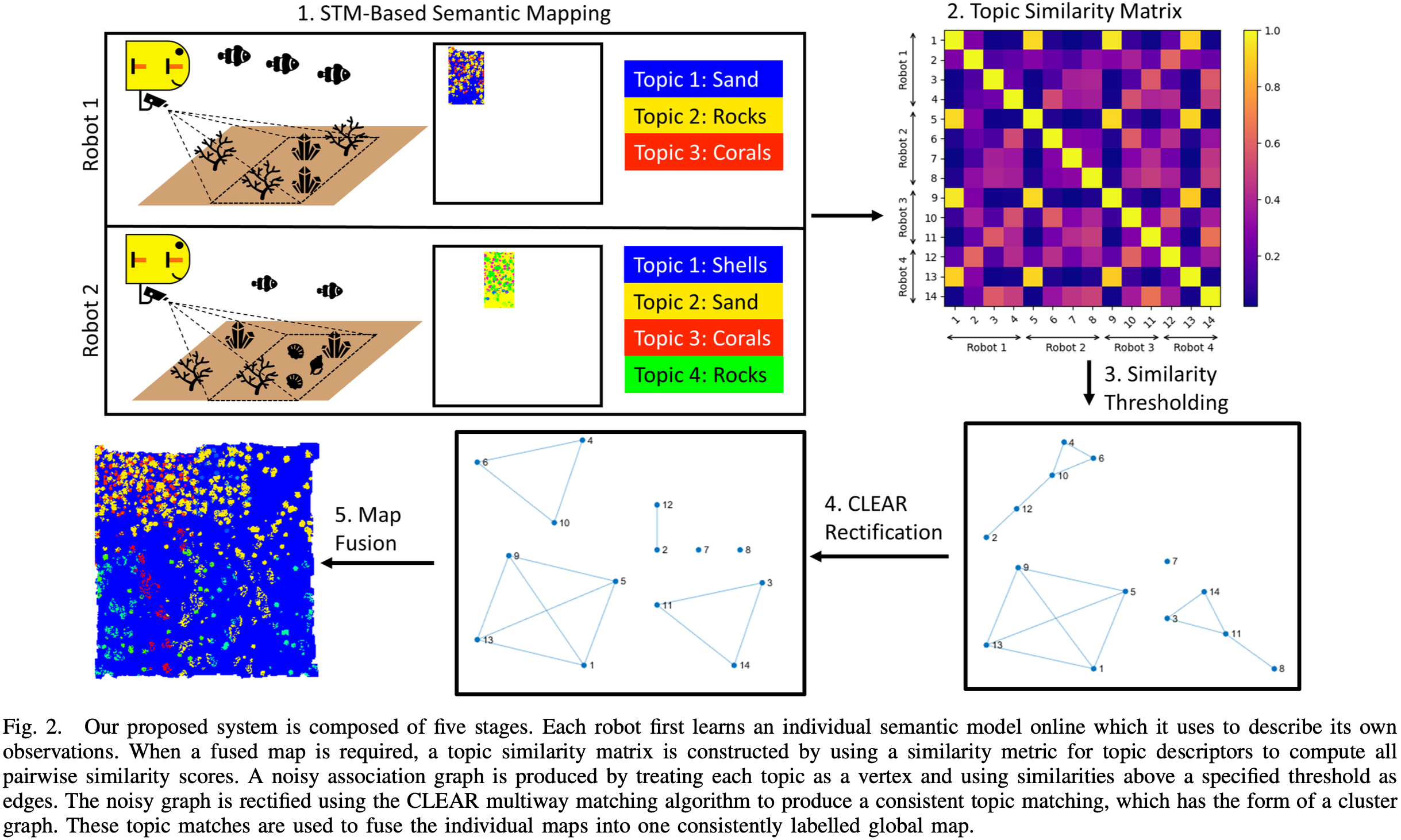
3.3　Constructing the Noisy Association Graph

实际中，相似性度量是有噪声的，因为认为具有相同语义的主题的相似性得分可能达不到 1.0，而语义非常不同的主题的相似性得分可能达不到 0.0。通过删除权重小于 σ∈(0,1)\sigma \in (0,1) 的边，并将权值大于 σ\sigma 的边设为 1，从而简化逐对相似度图，得到未加权的噪声关联图。

判断主题是否“足够相似”的阈值 σ\sigma 取决于相似性度量 ss、主题模型的超参数和主观判断等。选择 σ\sigma 的一个简单方案是收集过去任务中机器人开发的主题验证集，操作员推断它们的语义，然后调整 σ\sigma。实验发现阈值 σ=0.75\sigma = 0.75 对两种主题相似性度量都很有效。

3.4　Rectifying the Noisy Association Graph

当可视化为顶点表示主题、边表示匹配时，一致的匹配具有集群图的结构。这是一个由不相交的全连接分量组成的图，因此同一个分量中的任意两个主题都是匹配的，分量之间没有主题匹配。在这个聚类图中，整个机器人队开发的不同主题标签的数量等于不相交组件的数量。

CLEAR[3] 是一种谱聚类算法，用于估计与噪声关联图最近的聚类图（如图-2）。噪声关联图的拉普拉斯算子 LL 由邻接矩阵和度矩阵组成 L=D−AL = D - A：

[A]ij={1,s(ϕ1,ϕ2)≥σ0,otherwise(3)[A]_{ij} = \begin{cases} 1, &s(\phi_1, \phi_2) \ge \sigma \\ 0, &\text{otherwise} \end{cases} \tag{3}

[D]ij={∑k=1N[A]ik,i=j0,otherwise(4)[D]_{ij} = \begin{cases} \sum_{k=1}^N [A]_{ik}, &i = j \\ 0, &\text{otherwise} \end{cases} \tag{4}

CLEAR 使用一种特殊的基于度矩阵的拉普拉斯归一化，记为 LnrmL_{nrm}，以识别噪声关联图中具有高成对相似性的语义标签簇。LnrmL_{nrm} 值小于 0.5 的特征值的个数是对全局标签个数 ∣ZtG∣| \mathcal{Z}_t^G | 的稳健估计。CLEAR 然后使用 LnrmL_{nrm} 的特征向量来找到一致的标签对应关系集 Πt\Pi_t。

4　Experimental Methodology

使用珊瑚自动生成器包在虚幻引擎中制作的两个模拟环境，模拟环境如图-3。

在每个实验中，由 12 个模拟机器人组成的团队穿过环境，每个机器人使用 AirSim 收集了 250 个 RGB-D 观测值。AirSim 还为每个图像提供了 GT 语义分割。每个机器人都被给予无噪声的定位信息，并运行一个名为“Sunshine”的 BNP-ROST[4] 时空主题模型。实验中，随机选择 1 到 12 个机器人的局部地图，并进行融合，每个实验重复 24 次。

4.1　Evaluation Semantic Map Quality

合适的融合地图 g(x)g(x) 是一个在每个位置 xx 上，对操作员定义的真实标签的 f(x)f(x) 的良好预测。使用 AMI（Adjusted Mutual Information）来衡量预测结果，AMI 是 MI 的一种变体。MI 表示一个随机变量中包含的描述另一个随机变量的信息位数，对于离散随机变量 U∈U,V∈VU \in \mathcal{U}, V \in \mathcal{V}：

MI⁡(U,V)=∑u∈U∑v∈Vp(u,v)log⁡(p(u)p(v)p(u,v))(5)\operatorname{MI}(U, V) = \sum_{u \in \mathcal{U}} \sum_{v \in \mathcal{V}} p(u, v) \log \left( \frac{p(u) p(v)}{p(u, v)} \right) \tag{5}

给定语义地图 ff，gg 和有限单元格集 B\mathcal{B}，定义随机变量 BB 为从 B\mathcal{B} 均匀采样得到的单元格，定义随机变量 Yf=f(B),Yg=g(B)Y_f = f(B), Y_g = g(B) 为机器人队和 GT 对 BB 的语义标签。这些随机变量的联合概率为：

p(yf,yg)=1∣B∣∑b∈B1f(b)=yf∧g(b)=yb(6)p(y_f, y_g) = \frac{1}{| \mathcal{B} |} \sum_{b \in \mathcal{B}} \mathbb{1}_{f(b) = y_f \wedge g(b) = y_b} \tag{6}

定义熵 H(Yf),H(Yg)H(Y_f), H(Y_g)，则：

AMI⁡(Yf,Yg)=MI⁡(Yf,Yg)−E[MI⁡(Yf,Yg)]max⁡{H(Yf),H(Yg)}−E[MI⁡(Yf,Yg)](7)\operatorname{AMI}(Y_f, Y_g) = \frac{\operatorname{MI}(Y_f, Y_g) - \mathbb{E}[\operatorname{MI}(Y_f, Y_g)]}{\max \lbrace H(Y_f), H(Y_g) \rbrace - \mathbb{E}[\operatorname{MI}(Y_f, Y_g)]} \tag{7}

好的 AMI 得分为 1，表明机器人队的语义地图包含重现同一区域的 GT 语义地图所需的所有信息。如果融合的语义地图相对于 GT 具有较高的 AMI 分数，则机器人团队使用的每个语义标签与用于生成地面真值地图的每个标签之间存在一致的对应关系。

4.2　Baseline Comparisons

局部地图使用基于 ID 的匹配和匈牙利算法进行[5] 融合：

  • 基于 ID 的匹配假设每个机器人以相同的顺序观察相同的现象，因此一个机器人学习的第一个主题对应于其他每个机器人学习的第一个主题，其余主题也是如此。
  • 匈牙利算法只假设每个机器人观察到相同的现象，并找到第一个机器人的主题和每个额外机器人的主题之间的最大相似排列。

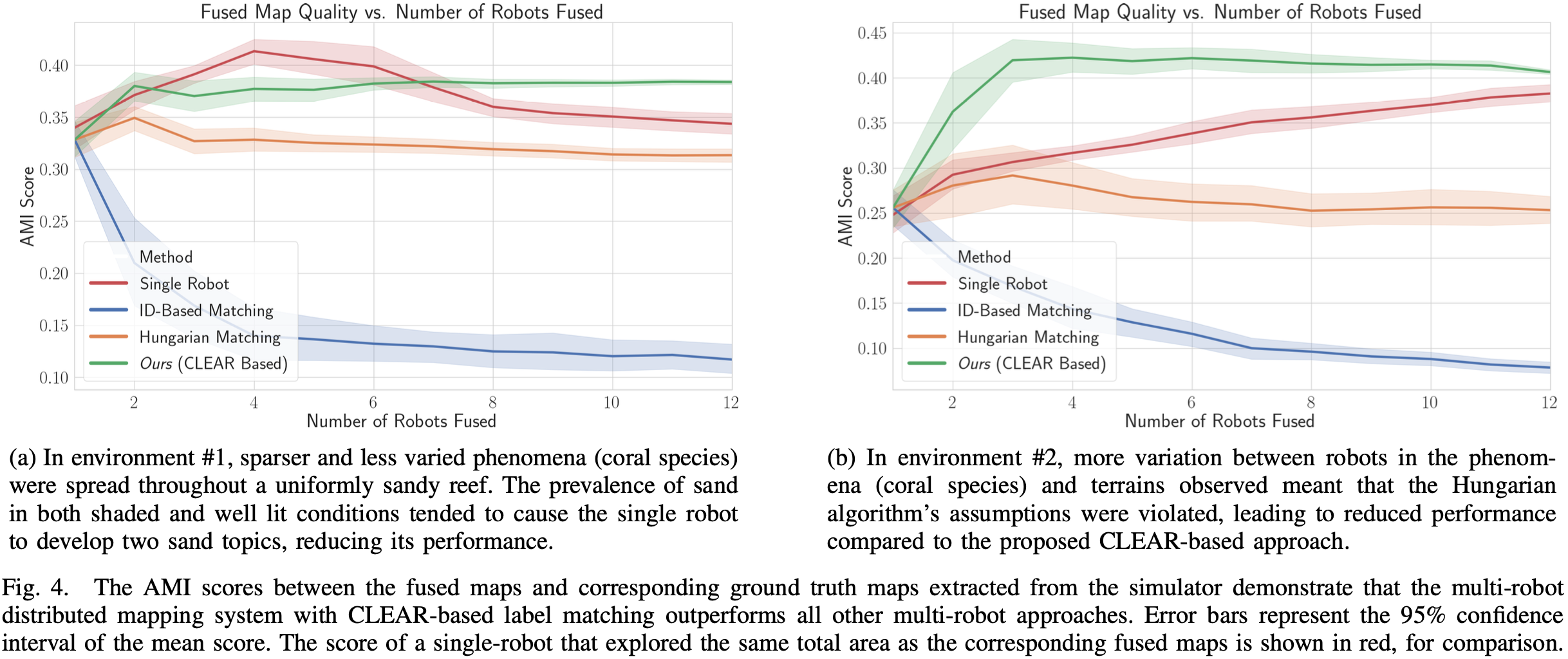
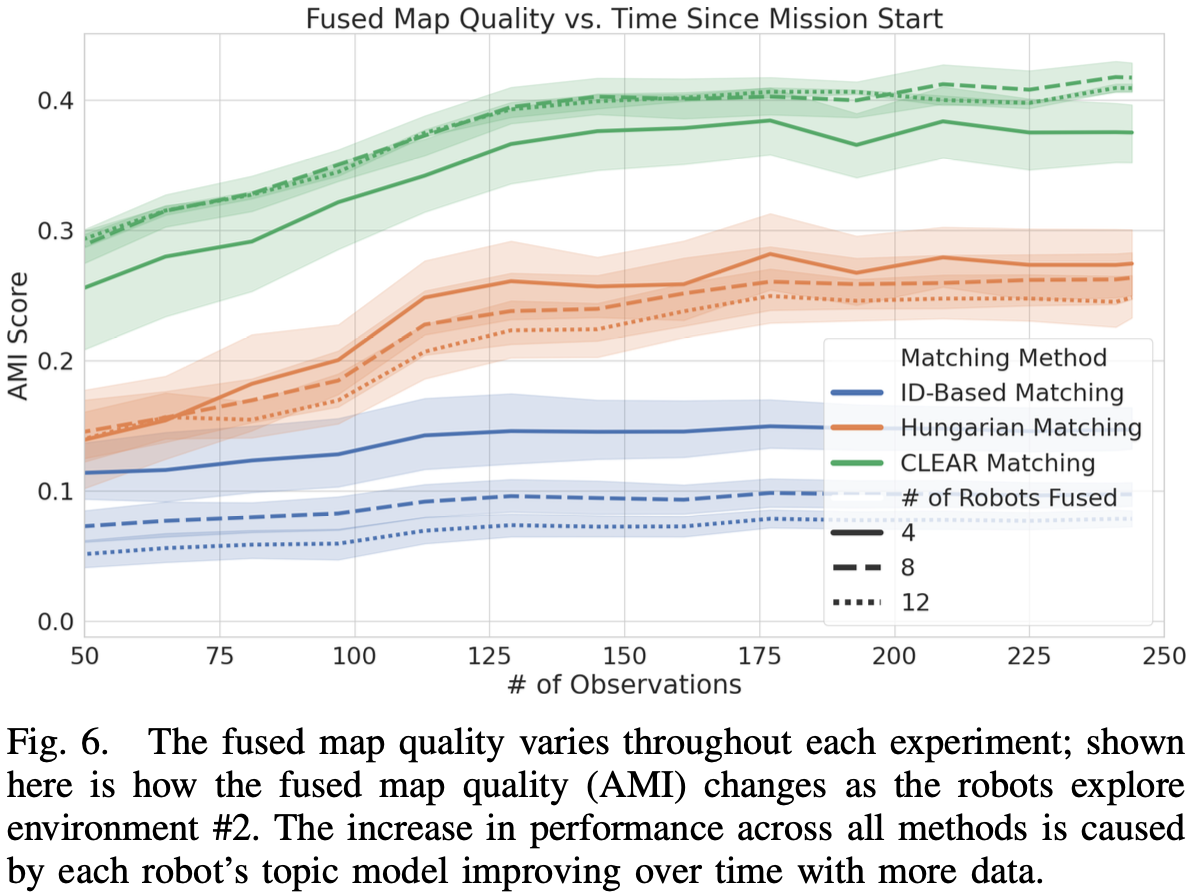
5　Results & Discussion

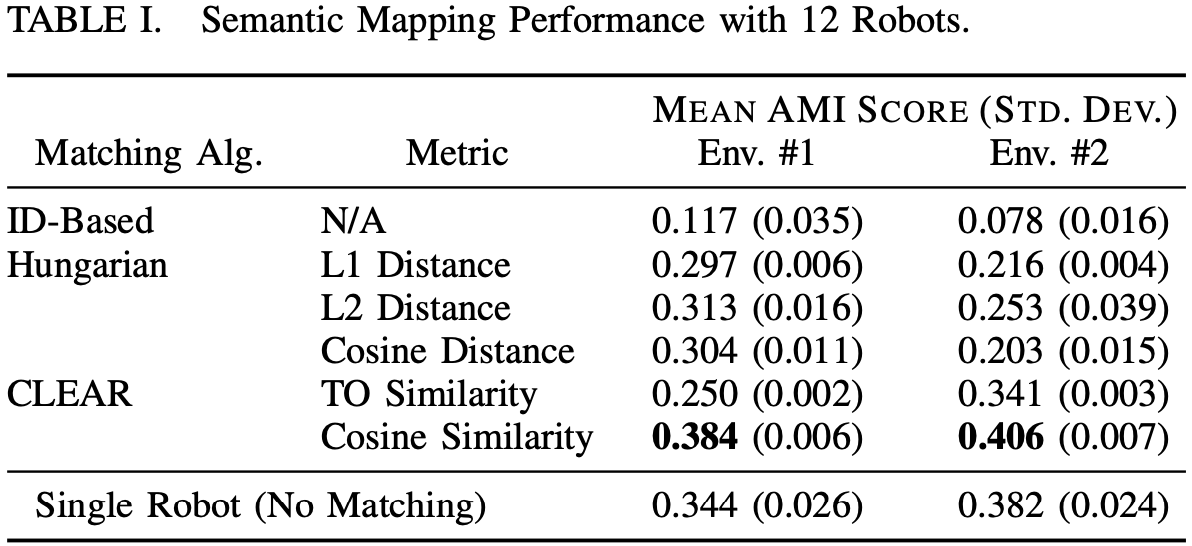
参考

  • [1] Y. Girdhar and G. Dudek, “Modeling curiosity in a mobile robot for long-term autonomous exploration and monitoring,” Autonomous Robots, vol. 40, no. 7, pp. 1267–1278, 2016, arXiv: 1509.07975 Publisher: Springer US.
  • [2] D. A. Levin, Y. Peres, and E. L. Wilmer, Markov Chains and Mixing Times, second edition, 2nd ed. American Mathematical Society, 2017.
  • [3] K. Fathian, K. Khosoussi, Y. Tian, P. Lusk, and J. P. How, “CLEAR: A Consistent Lifting, Embedding, and Alignment Rectification Algorithm for Multi-View Data Association,” arXiv:1902.02256 [cs], July 2019, arXiv: 1902.02256.
  • [4] Y. Girdhar and G. Dudek, “Modeling curiosity in a mobile robot for long-term autonomous exploration and monitoring,” Autonomous Robots, vol. 40, no. 7, pp. 1267–1278, 2016, arXiv: 1509.07975 Publisher: Springer US.
  • [5] K. Doherty, G. Flaspohler, N. Roy, and Y. Girdhar, “Approximate Distributed Spatiotemporal Topic Models for Multi-Robot Terrain Characterization,” in Intelligent Robots and Systems (IROS), 2018.