RF-LIO

Posted on Edited on In Waline:

对论文 RF-LIO: Removal-First Tightly-coupled Lidar Inertial Odometry in High Dynamic Environments (IROS, 2021) 的阅读整理。

RF-LIO

0 论文详情

  • 题目：RF-LIO: Removal-First Tightly-coupled Lidar Inertial Odometry in High Dynamic Environments
  • 作者：Chenglong Qian，Zhaohong Xiang，Zhuoran Wu，Hongbin Sun
  • 会议：IROS 2021

1 介绍

传统的主流 SLAM 算法是在环境相对静止的假设上推导进行的。然而事实上，真实的环境当中存在很多的动态物体，如车辆和行人等。由于传感器等视觉域被阻碍（field of view，FOV），导致大量的特征点落在了动态物体而非静态地图上，如图-1 所示，这将使得传统的基于静态环境假设的方法（LOAM、LIO-SAM 等）失效。同时，动态物体可能会遮挡路标、信号灯和其他一些点云地图中的重要静态特征，给识别带来挑战。因此，需要提高 SLAM 在动态环境中的鲁棒性。

图-1 特征点落在了动态物体上

一个动态 SLAM 的简单解决方案就是构建一个仅包含静态物体的地图，即将动态物体从点云中移除，例如 SuMa++ 算法。然而，这种方法在高动态的环境下缺乏稳定性，大量的动态物体会导致 scan-match 方法失效。同时，这种简单的方法依赖于深度学习算法，而深度学习严重依赖于训练集，这同样会限制 SuMa++ 算法的应用。

本文提出了一种新的先移除（removal-first）的紧耦合 LiDAR 惯导框架 RF-LIO，用于解决高动态环境下的 SLAM 问题。Removal-first 表达的是 RF-LIO 将先不依赖精确位姿来移除动态物体，然后执行 scan-match：

  1. 当新的 scan 到达，RF-LIO 不直接执行 scan-match 计算位姿。相反，使用紧耦合的 IMU 里程计去获取一个粗略的初始状态估计。
  2. RF-LIO 利用自适应分辨率距离图像初步去除环境中的动态点。
  3. 移除动态点后，RF-LIO 使用 scan-match 获得相对更加精确的位姿。

2 RF-LIO

2.1 系统概览

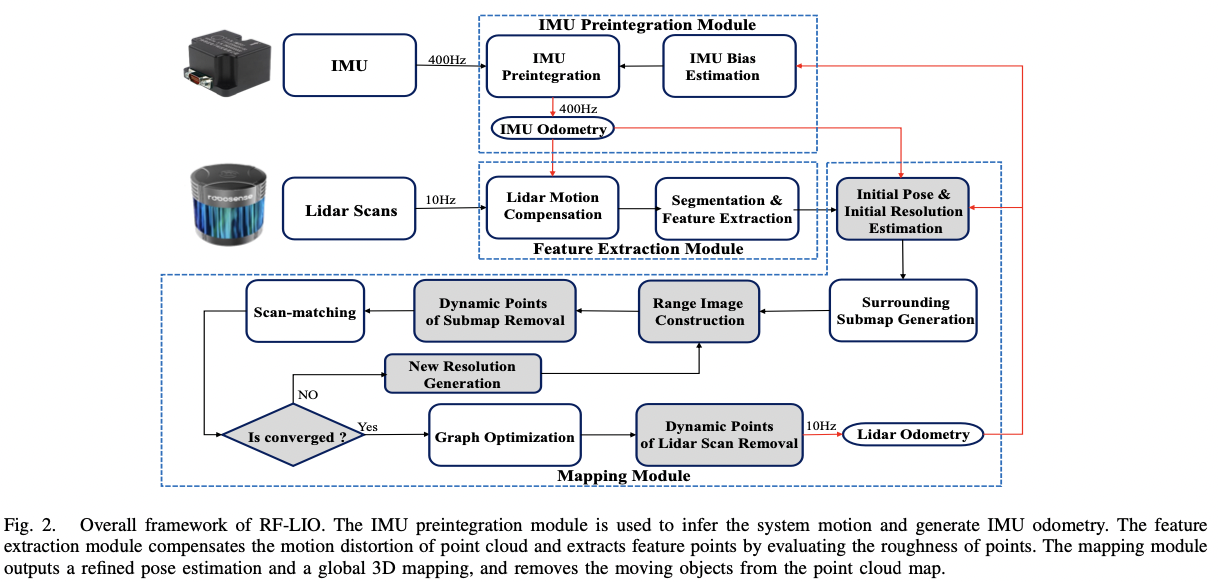
图-2 系统概览

RF-LIO 包含三个主要模块：IMU 预融合（IMU Preintegration）、特征提取（feature extraction）、建图（mapping）。首先，IMU 预融合推断系统运动并产生 IMU 数据。然后，特征提取补偿点云的运动畸变，并提取边特征和面特征。

建图模块则是 RF-LIO 的重要组成部分。为实现无精确位姿的动态物体先移除，需要几个关键步骤：

  1. 通过 IMU 获取初始位姿。然后 IMU 预融合和 scan-match 之间的误差用于确定初始分辨率（即每一个像素关联多少 FOV 角）。
  2. RF-LIO 使用初始分辨率从当前 LiDAR scan 及其对应的子图构建范围图（range image）。
  3. 通过比较能见度（visibility），可以移除子图中的主要动态点。
  4. 将 LiDAR 和 scan 匹配，然后判断 scan-match 是否收敛：如果收敛，则在图优化后，用最终良好的分辨率移除当前帧剩余的动态点；否则，生成新的分辨率，重复执行 2、3、4 步。

2.2 IMU 预融合和初始位姿

设世界坐标系为 WW，设 IMU 坐标系（与机器人坐标系相一致）为 BB。系统状态可以表示为：

x=[RT,pT,vT,bT]Tx = [R^T, p^T, v^T, b^T]^T

其中 R∈SO(3)R \in SO(3) 为旋转矩阵，p∈R3p \in \mathbb{R}^3 为位置向量（位移），vv 为速度向量，bb 为 IMU 偏差向量，由加速度计偏差 BaB^a 和陀螺仪偏差 BgB^g 组成。IMU 测量模型可以表示为：

ω^B(t)=ωB(t)+bg(t)+ηg(t)a^B(t)=RWBT(t)(aB(t)−gW)+ba(t)+ηa(t)\begin{aligned} \hat{\omega}_B (t) &= \omega_B (t) + b^g (t) + \eta^g (t) \\ \hat{a}_B (t) &= R^T_{WB} (t) (a_B(t) - g_W) + b^a (t) + \eta^a (t) \end{aligned}

其中 ω^B(t),a^B(t)\hat{\omega}_B (t), \hat{a}_B (t) 为在坐标系 BB 中的原始 IMU 测量数据，受到偏差 bb 和白噪声 η\eta 的影响。

当 IMU 测量数据到来时，使用 IMU 预融合方法[1]^{[1]}来从前面的关键帧 kk 来获取当前关键帧 k+1k+1 的初始位姿：

RWBk+1=RWBkΔRk,k+1Exp(JΔRgbkg)vBk+1=vBk+gWΔtk,k+1+RWBk(ΔvBk,k+1+JΔvgbkg+JΔvabkg)pBk+1=pBk+vBkΔtk,k+1+12gWΔtk,k+12+RWBk(Δpk,k+1+JΔpgbkg+JΔpabka)\begin{aligned} R_{WB}^{k+1} &= R_{WB}^k \Delta R_{k,k+1} Exp(J^g_{\Delta R} b_k^g) \\ v_B^{k+1} &= v_B^k + g_W \Delta t_{k,k+1} + R_{WB}^k (\Delta v_B^{k,k+1} + J^g_{\Delta v} b_k^g + J_{\Delta v}^a b_k^g) \\ p_B^{k+1} &= p_B^k + v_B^k \Delta t_{k,k+1} + {1 \over 2} g_W \Delta t_{k,k+1}^2 + R_{WB}^k (\Delta p_{k,k+1} + J_{\Delta p}^g b_k^g + J_{\Delta p}^ a b_k^a) \end{aligned}

其中 Jacobian 矩阵 J(⋅)abaJ_{(\cdot)}^a b^a 和 J(⋅)gbgJ_{(\cdot)}^g b^g 表示在不明确地重新计算预积分的情况下改变偏差影响的一阶近似。

2.3 IMU 预融合误差和初始分辨率

在使用 IMU 测量推测系统运动时，将不可避免地与 ground truth 有所偏离，使得查询 scan 点到对应地图点时产生模糊。RF-LIO 使用 IMU 预融合和 scan-match 之间的位姿误差来动态生成初始分辨率。

IMU 预融合的平移和旋转误差可以定义为：

ERk=Log((ΔRk−1,kExp(JΔRgbk−1g))TRBWk−1RWBk)Evk=RBWk−1(vBk−vBk−1−gWΔtk−1,k)−(Δvk−1,k+JΔvgbk−1g+JΔvabk−1a)Epk=RBWk−1(pBk−pBk−1−vBk−1Δtk−1,k−12gWΔtk−1,k2)−(Δpk−1,k+JΔpgbk−1g+JΔpabk−1a)Ebk=bk−bk−1\begin{aligned} E_R^k &= Log((\Delta R_{k-1,k} Exp(J_{\Delta R}^g b_{k-1}^g))^T R_{BW}^{k-1} R_{WB}^k) \\ E_v^k &= R_{BW}^{k-1} (v_B^k - v_B^{k-1} \\ &- g_W \Delta t_{k-1,k}) - (\Delta v_{k-1,k} + J_{\Delta v}^g b_{k-1}^g + J_{\Delta v}^a b_{k-1}^a) \\ E_p^k &= R_{BW}^{k-1} (p_B^k - p_B^{k-1} - v_{B}^{k-1} \Delta t_{k-1,k} - {1 \over 2} g_W \Delta t_{k-1,k}^2) \\ &- (\Delta p_{k-1,k} + J_{\Delta p}^g b_{k-1}^g + J_{\Delta p}^a b_{k-1}^a) \\ E_b^k &= b_k - b_{k-1} \end{aligned}

通过上式可以计算之前关键帧第 kk 的位姿误差。然而在 scan-match 前，当前第 k+1k+1 帧的 IMU 预融合误差无法通过上式获得。为得到第 k+1k+1帧的误差，使用如下的误差转换关系：

δXk=δXk−1+δX˙k−1Δt\delta X_k = \delta X_{k-1} + \delta \dot{X}_{k-1} \Delta t

由于只关心 δX\delta X 中的 δθ\delta \theta 和 δp\delta p 部分，因此有下式：

[δθk+1δpk+1]=A[δθkδpkδvkδbkaδbkg]+B[δηgδηaδηbgδηba]A=[I−[ω]×Δt000−IΔt0IIΔt00]B=[IΔt0000000]\begin{aligned} & \left[ \begin{matrix} \delta \theta^{k+1} \\ \delta p^{k+1} \end{matrix} \right] = A \left[ \begin{matrix} \delta \theta^k \\ \delta p^k \\ \delta v^k \\ \delta b_k^a \\ \delta b_k^g \end{matrix} \right] + B \left[ \begin{matrix} \delta \eta^g \\ \delta \eta^a \\ \delta \eta_{b^g} \\ \delta \eta_{b^a} \end{matrix} \right] \\ & A = \left[ \begin{matrix} I - [\omega]_{\times} \Delta t &0 &0 &0 &-I \Delta t \\ 0 &I &I \Delta t &0 &0 \end{matrix} \right] \\ & B = \left[ \begin{matrix} I \Delta t &0 &0 &0 \\ 0 &0 &0 &0 \end{matrix} \right] \end{aligned}

通过预测 IMU 里程定位误差，可以获得 range image 的初始分辨率。使用下面的经验式来转换平移和旋转误差为分辨率：

r=αδp+δθr = \alpha \delta p + \delta \theta

其中 α\alpha 介于 0 和 1 之间，用于平衡两个误差对分辨率的影响。设置最小分辨率 r0r_0 并适当则大预测的分辨率 rr，最终初始分辨率 rfr_f 定义为：

rf=max⁡(βr,r0)r_f = \max (\beta r, r_0)

其中 β\beta 为大于 1 的系数，而

r0=vertical FOVvertical raysr_0 = {\mathrm{vertical\ FOV} \over \mathrm{vertical\ rays}}

2.4 构建 range image 及移除动态点

定义 Fk+1F_{k+1} 为当前帧的 scan，MkM_k 为对应的子图，是一个点云图并由在 Fk+1F_{k+1} 上执行滑动窗口算法得到。为平衡动态点的移除率以及实时性能，使用一个完全的查询 scan 来与特征子图比较。因为一个有多个关键帧的特征子图与一个完全的查询 scan 有相近的深度，且包含的点比完整子图少。然后将点云分为两个互斥集：动态点集 (⋅)D(\cdot)^D 和静态点集 (⋅)S(\cdot)^S，即有：

M=MD∪MSF=FD∪FS(⋅)D∩(⋅)S=∅\begin{aligned} & M = M^D \cup M^S \\ & F = F^D \cup F^S \\ & (\cdot)^D \cap (\cdot)^S = \emptyset \end{aligned}

通过投影 range image 的 visiblity 来辨别动态点。

图-3 识别动态点

如图-3，range image 中像素 (i,j)(i,j) 的值 Ik+1,ijI_{k+1,ij} 定义为点 p∈R3p \in \mathbb{R}^3 到第 k+1k+1 个关键帧的局部坐标系 Bk+1B_{k+1} 的距离：

Ik,ijM=min⁡p∈PijMdist(p)Ik+1,ijF=min⁡p∈PijFdist(p)\begin{aligned} I_{k,ij}^M &= \min_{p \in P_{ij}^M} \mathrm{dist}(p) \\ I_{k+1,ij}^F &= \min_{p \in P_{ij}^F} \mathrm{dist}(p) \end{aligned}

Range image 的大小由给定的分辨率和 LiDAR 的水平和垂直 FOV 范围决定。PijM or FP_{ij}^{M\ \mathrm{or}\ F} 为点 PM or FP^{M\ \mathrm{or}\ F} 的球坐标系（方位角 ii 和俯仰角 jj）。

子图的点和 scan 的点的 visibility 通过矩阵相减得到：

Ik+1Diff=Ik+1F−Ik+1MI_{k+1}^{\mathrm{Diff}} = I_{k+1}^F - I_{k+1}^M

如果点 p∈PijM or Fp \in P_{ij}^{M\ \mathrm{or}\ F} 在 Ik+1DiffI_{k+1}^{\mathrm{Diff}} 的对应像素值大于阈值 τ\tau，则该点为动态点：

MkD={Mk∣Ik+1Diff>τ}Fk+1D={Fk+1∣Ik+1Diff<−τ}τ=γdist(p)\begin{aligned} M_k^D &= \{ M_k | I_{k+1}^{\mathrm{Diff}} > \tau \} \\ F_{k+1}^D &= \{ F_{k+1} | I_{k+1}^{\mathrm{Diff}} < -\tau \} \\ \tau &= \gamma \mathrm{dist} (p) \end{aligned}

其中 γ\gamma 为与点距离相关的敏感度，设置为图-5 中 final resolution 的最大值。

2.5 LiDAR 里程和新分辨率

LiDAR 里程用于估计两个连续 scan 的传感器运动。使用 LOAM 中的方法。为每一个新 scan 通过计算点在局部区域点 roughness 提取边特征和面特征。定义第 k+1k+1 个关键帧边和面特征为 Fk+1eF_{k+1}^e 和 Fk+1pF_{k+1}^p。然后将这些特征从坐标系 Bk+1B_{k+1} 转换到全局坐标系 WW 得到 {wFk+1e,wFk+1p}\{ {}^w F_{k+1}^e, {}^w F_{k+1}^p \}。初始转换由 IMU 预融合获得。对于每个 {wFk+1e,wFk+1p}\{ {}^w F_{k+1}^e, {}^w F_{k+1}^p \} 中的特征点，可以通过最近邻搜索找到其在 {Mke,Mkp}\{ M_{k}^e, M_{k}^p \} 中对应的特征。用下式定义点到其对应点的距离：

dke=∣(pk+1,ie−pk,je)×(pk+1,ie−pk,le)∣∣pk+1,je−pk,le∣dkp=∣(pk+1,ip−pk,jp)(pk,jp−pk,lp)×(pk,jp−pk,mp)∣∣(pk,jp−pk,lp)×(pk,jp−pk,mp)∣\begin{aligned} d_k^e &= {|(p_{k+1,i}^e - p_{k,j}^e) \times (p_{k+1,i}^e - p_{k,l}^e)| \over |p_{k+1,j}^e - p_{k,l}^e|} \\ d_k^p &= {|(p_{k+1,i}^p - p_{k,j}^p) (p_{k,j}^p - p_{k,l}^p) \times (p_{k,j}^p - p_{k,m}^p)| \over |(p_{k,j}^p - p_{k,l}^p) \times (p_{k,j}^p - p_{k,m}^p)|} \end{aligned}

i,j,l,mi,j,l,m 为点索引，pk+1,ie∈wFk+1ep_{k+1,i}^e \in {}^w F_{k+1}^e 为点特征点，pk,je,pk,le∈Mkep_{k,j}^e, p_{k,l}^e \in M_k^e 为对应的边特征，同理于面特征点。最终可以通过优化下问题获得位姿变换：

min⁡ΔTk,k+1=min⁡ΔTk,k+1∑pk+1,ie∈wFk+1edke+∑pk+1,ip∈wFk+1pdkp\min \Delta T_{k,k+1} = \min_{\Delta T_{k,k+1}} \sum_{p_{k+1,i}^e \in {}^w F_{k+1}^e} d_k^e + \sum_{p_{k+1,i}^p \in {}^w F_{k+1}^p} d_k^p

当 scan-match 收敛时，可以得到关键帧 kk 和 k+1k+1 间的相对位姿变换 ΔTk,k+1\Delta T_{k,k+1}。因此，LiDAR 里程为：

Tk+1=TkΔTk,k+1T_{k+1} = T_k \Delta T_{k,k+1}

虽然去除了动态点，然而在有数个动态物体的高动态环境下，LiDAR 里程会产生漂移。这里给出一个简单但有效的解决方法，其由边特征点 Fk+1eF_{k+1}^e 的欧拉距离来进行判定。这种方法利用边特征点点稀疏性避免使用所有点计算的复杂度，同时具有好的兼容性。虽然需要额外的运算，但是能提供足够的效率。此算法定义如下：

图-4 收敛分数计算算法

其中 τD\tau_D 为去除奇异点的阈值。当 score<score0\mathrm{score < score_0}，则判断为收敛。如果 scan-match 无法收敛，则使用 2.3 部分中的方法基于 LiDAR 里程生成更好的初始分辨率，然后再一次移除动态点并重复 2.5 部分中的步骤。

3 实验

  • 参数设置：α=0.1,β=2.0,r0=0.02,γ=0.02,score0=0.25\alpha = 0.1, \beta = 2.0, r_0 = 0.02, \gamma = 0.02, score_0 = 0.25
  • 初始分辨率分析：
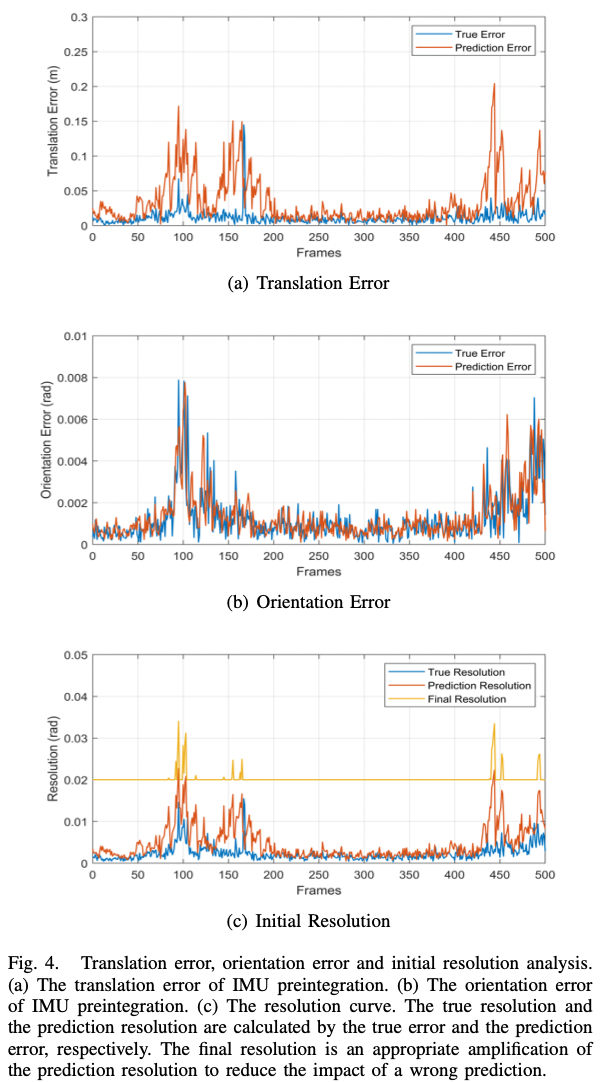
图-5 初始分辨率分析
  • 动态物体移除：
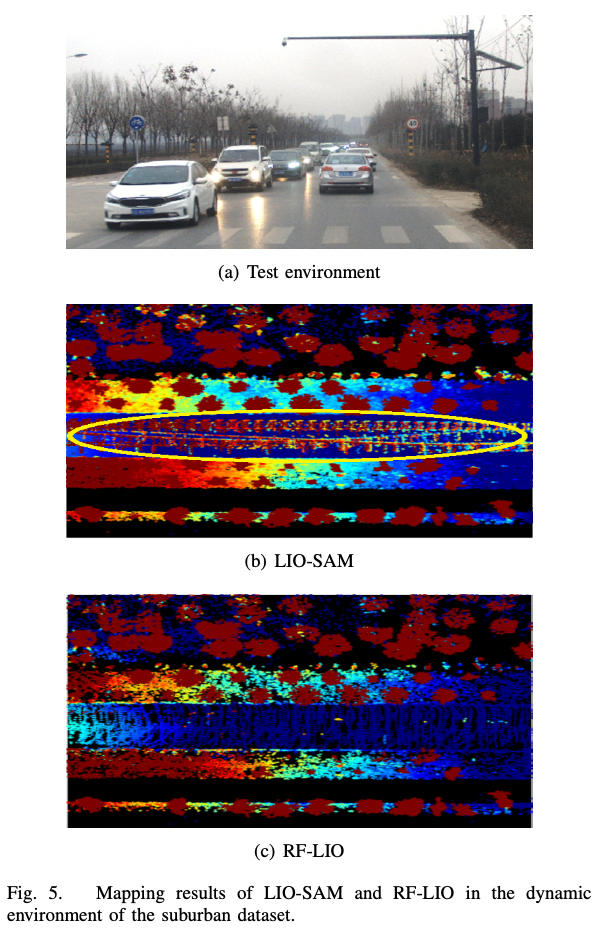
图-6 动态物体移除
  • 建图效果：
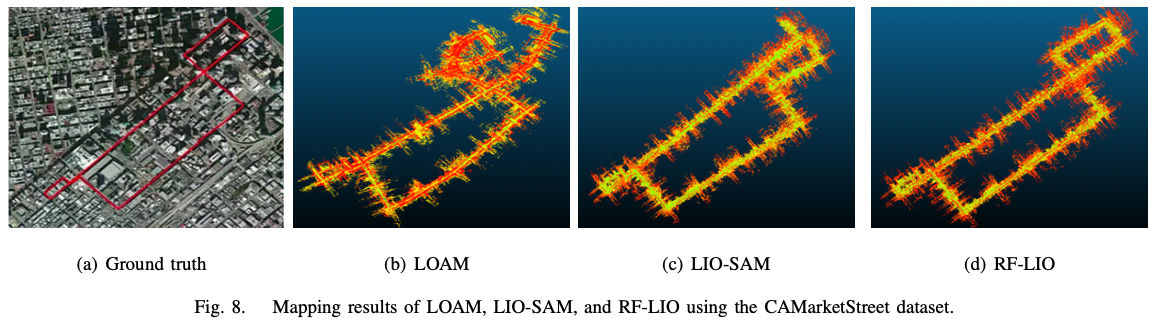
图-7 动态物体移除

参考

  • [1] C. Forster, L. Carlone, F. Dellaert, and D. Scaramuzza, “On-manifold preintegration theory for fast and accurate visual-inertial navigation,” IEEE Transactions on Robotics, pp. 1–18, 2015.