RP-VIO

对论文 RP-VIO: Robust Plane-based Visual-Inertial Odometry for Dynamic Environments (IROS, 2021) 的阅读整理。

RP-VIO

论文情况

• 标题：RP-VIO: Robust Plane-based Visual-Inertial Odometry for Dynamic Environments
• 作者：Karnik Ram, Chaitanya Kharyal, Sudarshan S. Harithas, K. Madhava Krishna
• 会议：IROS, 2021
• 源码：https://github.com/karnikram/rp-vio
• 官网：https://rebrand.ly/rp-vio

1 Introduction

传统 VINS 的缺点：

• 除需要精确同步和校准的额外硬件，系统还需要执行足够的旋转和加速度运动，以保持重力和尺度可观测。
• VINS 还需要在线校准，退化轨迹可能使外部和内在偏差不可观察。
• 在具有多个独立动态对象的环境中的性能较差。

考虑绕过语义，直接识别场景中的静态结构以进行特征跟踪。注意到，平面是人造环境中最丰富的静态区域，且提供了一种简单的几何形状，可以进一步用来改进估计。基于这一思考，提出了 RP-VIO。RP-VIO 仅使用由平面分割模型识别的场景中一个或多个平面的特征，并使用平面诱导的单应矩阵进行运动估计。

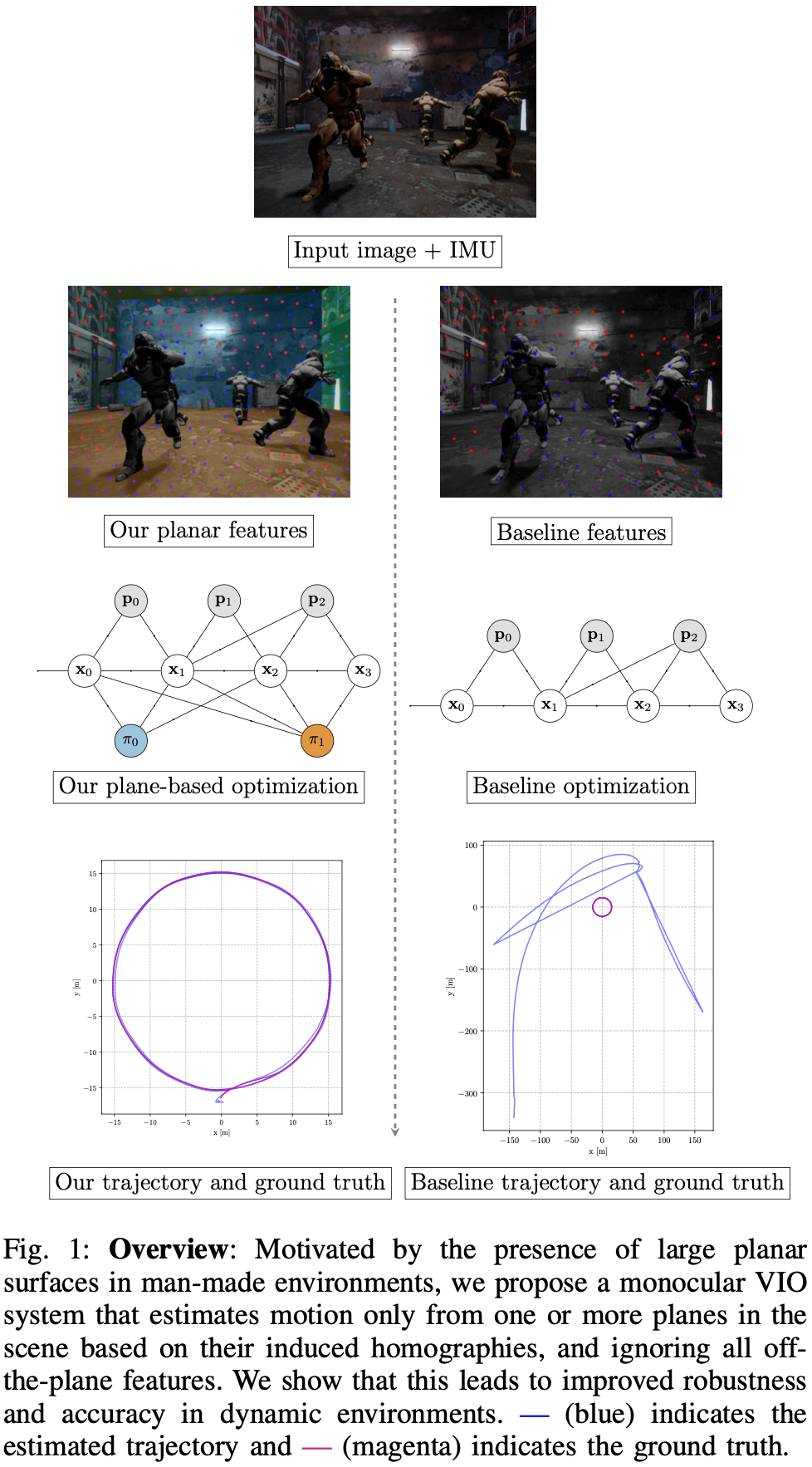
RP-VIO 的贡献如下：

• RP-VIO，一种单目 VIO 系统（基于 VINS- Mono），在初始化和滑动窗口估计期间仅使用平面特征及其诱导的单应性。
• 给出一个逼真的视觉惯性数据集，与现有数据集不同，它包含在整个序列中存在的动态物体，并具有足够的 IMU 数据。

2 Method

RP-VIO 基于 VINS-Mono 进行修改。认为 VINS-Mono 是一个纯粹的 VIO 系统，忽略其重定位和回环检测模块。在其前端基础上，仅检测和跟踪场景中的面特征，并将平面单应性约束引入其初始化和优化模块。

2.1 Definitions

$W$ 表示世界坐标系，z 轴沿重力方向朝下；$B$ 表示自身坐标系，与 IMU 帧一致；$C$ 表示相机坐标系；$B_i, C_i$ 表示 $t_i$ 时刻的自身、相机坐标系。

$\mathbf{T}_{ji}$ 为从 $t_j$ 到 $t_i$ 的变换矩阵；$\mathbf{T}_i$ 表示相对世界系的变换矩阵。

$\mathbf{u}^l$ 为第 $l$ 个视觉特征的 2D 图像坐标，对应的 3D 坐标 $\mathbf{p}_l$ 则由相对于其被第一次观测到时所在帧的逆深度 $\lambda_l$ 表示。平面 $\pi_p$ 表示为其相对于 $C_0$ 帧的法向量和距离 $(\mathbf{n}, d)$。将平面点从 2D 图像坐标系 $C_0$ 映射到 $C_j$ 的平面单应性矩阵为 $H_j$。单应性约束如图-2。

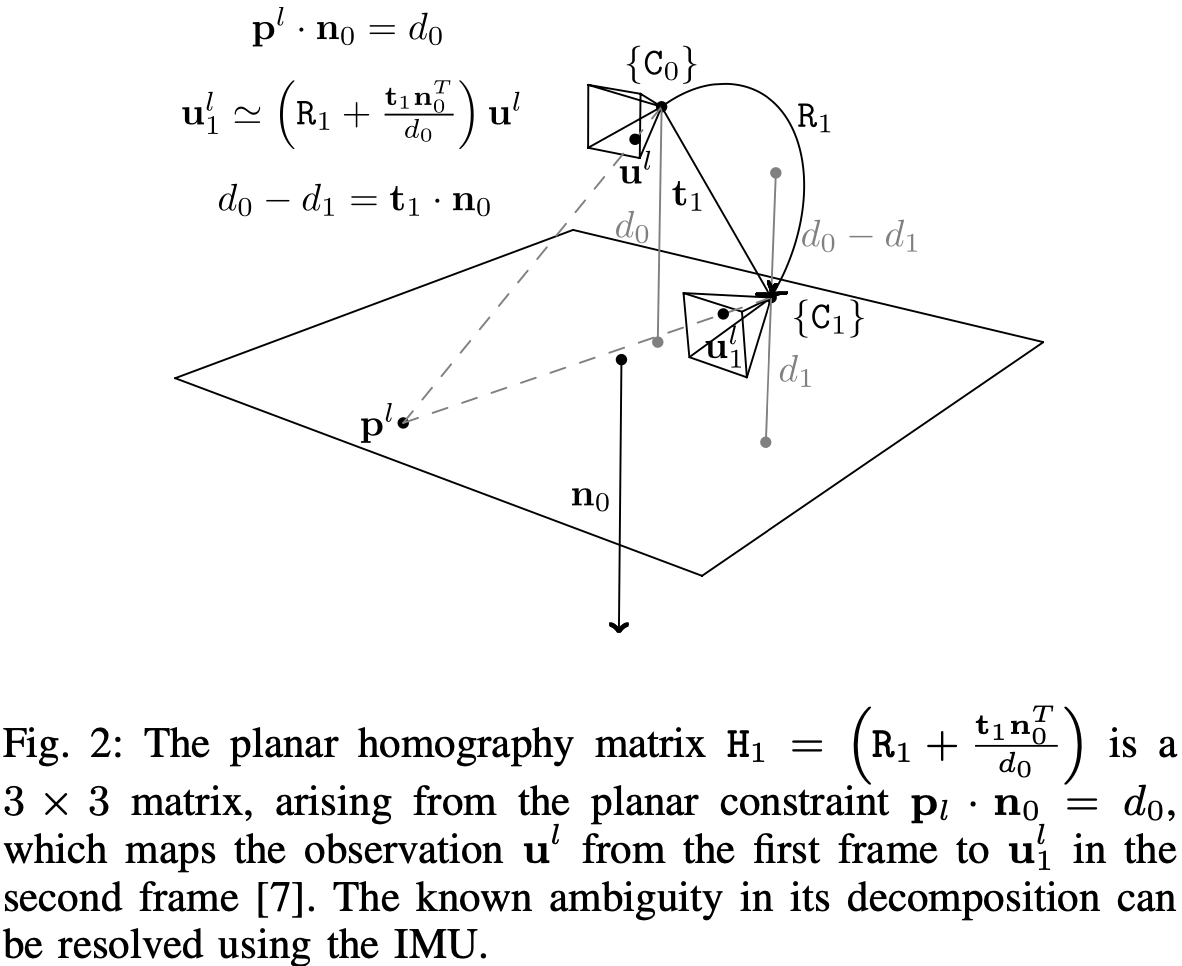
系统 $t_i$ 时刻的状态 $\text{x}_i$ 定义为 IMU 的位置、旋转、角速度、偏置、3D 点的逆深度和平面，即 $\text{x}_i = [\mathbf{R}_i, \mathbf{t}_i, \mathbf{v}_i, \mathbf{b}_i, \{ \lambda_l \}, \{ \pi_p \}]$。$\mathcal{X}$ 表示所有在滑动窗口 $\mathcal{K}$ 的帧的状态，即 $\mathcal{X} \doteq \{ \text{x}_i \}_{i \in \mathcal{K}}$。

2.2 Front-End

系统将灰度图、IMU 测量和平面分割掩码作为输入。平面分割掩码是从基于 CNN 的模型中获得，在后面内容中介绍。将得到的平面分割掩码作用于原始图像，仅检测和跟踪场景中属于（静态）平面区域的特征，同时保持每个被跟踪特征所属平面的信息。

为了避免在掩码边缘检测到任何可能属于动态对象的特征，对原始掩码进行腐蚀操作。然后，使用 RANSAC 对每个平面的特征分别拟合一个平面单应性模型，以剔除离群点；这些异常值可能是 KLT 光流算法错误匹配产生的特征，也可能是不属于较大父平面的不准确的片段所产生的特征。将图像帧之间的原始 IMU 测量值转换为预积分测量值，选择视差足够大、特征轨迹足够长的图像帧作为关键帧。

2.3 Initialization

主要的视觉惯性滑动窗口优化是非凸的，迭代最小化需要精确的初始估计。为了在不对初始设置做任何假设的情况下获得良好的初始估计，使用了一个单独的松耦合初始化过程，其中视觉测量和惯性测量被单独处理为各自的姿态估计，然后对齐在一起，以在多个步骤中求解未知数。

从初始图像帧窗口中选择视差足够大的 2 帧；在所有匹配特征中，只选择来自场景中最大平面的特征，即具有最大特征数量的平面。利用这些特征和 RANSAC 拟合出两帧姿态与最大平面之间的平面单应矩阵 $H$，该单应矩阵被归一化。

然后使用 Malis 和 Vargas[1] 的解析方法分解为旋转、平移和平面法向量。

然而，该方法最多返回 4 个不同的解，这些解必须简化为一个。首先通过正深度约束将该解决方案集减少为 2，即所有平面特征必须位于相机的前面，$\mathbf{n}_i^T \mathbf{u}_{\mu} > 0$（$\mathbf{u}_{\mu}$ 为标准化图像坐标下的平均 2D 特征点）。对于剩下的 2 个解，选择转换到 $B$ 系后旋转最接近对应 IMU 预积分的旋转 $\Delta \bar{\mathbf{R}}_{ij}$，即：

$\arg \min_k \| \Delta \bar{\mathbf{R}}_{ij}^T (\mathbf{R}_{BC} \mathbf{R}_{ij}^k \mathbf{R}_{BC}^T) - I \|^2 \tag{1}$

尽管预积分的 IMU 旋转部分中陀螺仪偏差还没有估计，但其大小通常太小，不会造成解决方案的差异。

然后，使用分解得到的估计姿态对两帧之间的特征 3D 位置进行三角剖分，获得初始点云。使用 PnP 估计窗口内剩余帧相对于该点云的姿态。注意到，由于两帧之间的估计姿态在平面距离 $d$ 的尺度内，三角化的点云和推导的姿态也在相同的尺度内。

然后将所有姿态估计输入到一个视觉 BA 求解器中，除了标准的 3D-2D 重投影残差外，还包括由平面单应性引起的 2D-2D 重投影残差：

$\mathbf{r}_{\mathcal{H}} = \mathbf{u}_j^l - \left( \mathbf{R}_j + \frac{\mathbf{t}_j \mathbf{n}^T}{d} \right) \mathbf{u}^l \tag{2}$

该残差度量 $C_j$ 帧中点 $\mathbf{p}_l$ 的期望观测值与真实观测值 $\mathbf{u}_j^l$ 之间的差异，$C_j$ 帧中点 $\mathbf{p}_l$ 是通过单应矩阵从第一帧中映射其对应的图像位置 $\mathbf{u}^l$ 得到的。图-2 也说明了这个过程。

BA 的输出是尺度为 $d$ 的相机姿态、3D 特征点、平面法线。这个未知的尺度 $d$，以及初始化主要优化所需的剩余未知数，如重力向量、速度和 IMU 偏差，使用与 VINS-Mono[2] 中相同的分治方法进行估计。

对于场景中最大平面以外的平面，包括可能新观测到的平面，同样计算它们各自的平面单应矩阵并将其分解。但避免进行另一轮的 BA 操作且将其姿态与 IMU 测量重新对齐，以估计各自的尺度因子 $d_p$。相反，将 $d_p$ 直接估计为每个分解的平移量 $\mathbf{t}_p$ 与对应的度量平移量 $\mathbf{t}$（前面使用最大的平面和惯性测量进行了估计）的反比。这样，状态中的所有视觉和惯性量都已经解决了，这些估计值被输入到滑动窗口估计器中作为优化的初始值。

2.4 Sliding-window Optimization

定义 $\mathcal{I}_{ij}$ 为滑动窗口 $\mathcal{K}$ 内两个连续帧之间的所有 IMU 测量；在帧 $i$ 中观测到的所有平面特征定义为 $\mathcal{C}_i$；所有观测到的平面为 $\mathcal{P}$。因子图如图-3 所示。

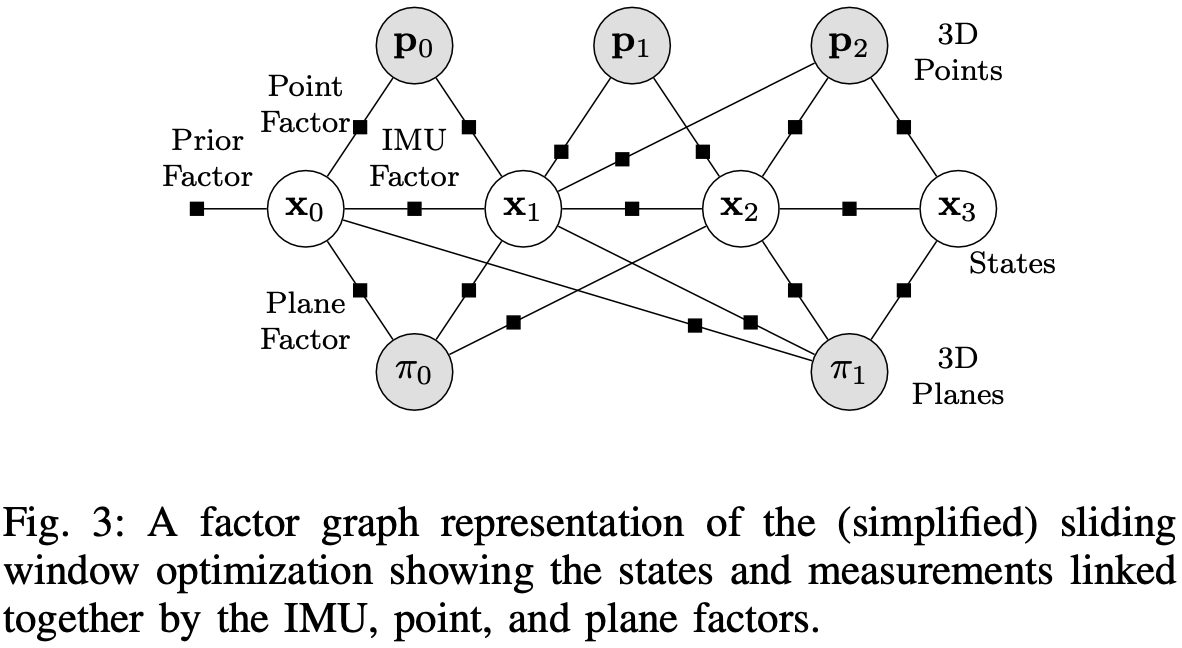
滑动窗口中的状态估计 $\mathcal{X}^*$ 由下式得到：

$\begin{aligned} \mathcal{X}^* &\doteq \arg \min_{\mathcal{X}} \| \mathbf{r}_p \|^2 + \sum_{(i,j) \in \mathcal{K}} \| \mathbf{r}_{\mathcal{I}_{ij}} \|^2 \\ &+ \sum_{i \in \mathcal{K}} \sum_{l \in \mathcal{C}_i} \rho(\| \mathbf{r}_{\mathcal{C}_{il}} \|^2) + \sum_{p \in \mathcal{P}} \sum_{i \in \mathcal{K}} \sum_{l \in \mathcal{C}_i} \rho(\| \mathbf{r}_{\mathcal{H}} \|^2) \end{aligned} \tag{2}$

$\mathbf{r}_p$ 为先验残差，来自于前一状态的边缘化；$\mathbf{r}_{\mathcal{I}_{ij}}$ 为预积分 IMU 残差；$\mathbf{r}_{\mathcal{C}_{il}}$ 为 VINS-Mono 中定义的 3D-2D 投影残差；$\rho$ 为柯西损失；$\mathbf{r}_{\mathcal{H}}$ 为平面单影损失，定义为：

$\mathbf{r}_{\mathcal{H}} = \mathbf{u}_j^l - \mathbf{T}_{BC}^{-1} \left( \mathbf{R}_{ji} + \frac{\mathbf{t}_{ji} (\mathbf{n}_i^p)^T}{d_i^p} \right) \mathbf{T}_{BC} \mathbf{u}_i^l \tag{4}$

第 $p$ 个平面的法向量 $\mathbf{n}^p$ 和深度 $d^p$ 在 $C_0$ 中被最初定义，并通过 (5) 转换到 $B_i$：

$\begin{aligned} \mathbf{n}_{B_i} &= \mathbf{R}_i^T \mathbf{R}_{BC} \mathbf{n}_{C_0} \\ d_{B_0} &= d_{C_0} + \mathbf{t}_{BC} \cdot \mathbf{n}_{B_0} \\ d_{B_i} &= d_{B_0} - \mathbf{t}_{B_0 B_i} \cdot \mathbf{n}_{B_0} \end{aligned} \tag{5}$

整个非线性目标函数使用 Ceres Solver 中的 Dogleg 算法和 Dense-Schur 线性求解器迭代最小化。

在优化结束时，窗口向前移动一帧以合并最新一帧。通过传播前一帧的惯性测量值来初始化最新一帧的状态。

2.5 Plane Segmentation

为了从每个输入的 RGB 图像中分割出平面，使用 Plane-Recover[3] 模型。模型同时预测平面分割掩码及其 3D 参数。该模型在单个 Nvidia GTX Titan X (Maxwell) GPU 上以 30 FPS 的速度运行。

在实验中注意到，预测的分割通常是不连续的，且单个大平面被分割为多个独立的平面。为克服这一问题，引入了一个额外的平面间损失函数，将具有较小相对方向的平面约束为单个平面：

$\mathcal{L}_{\text{inter}} = \frac{1}{n} \sum_{i=1}^n \sum_{j=1}^m \| \mathbf{n}_i^j \cdot \mathbf{n}_i^j - l_i \|^2 \tag{6}$

$\mathbf{n}$ 为平面法向量，$m$ 为平面总数（固定为 3），$n$ 为一批次中的图像数，$l_i$ 为生成的平面间标签，如果 $\angle (\mathbf{n}_i^j, \mathbf{n}_i^j) < \pi/4$ 则为 1，否则为 0。

用 SYNTHIA 提供的训练数据、室内 ScanNet 数据集的两个额外序列 (00,01) 上进行训练。图-5 为真实世界的分割结果。

3 Experiments

• 硬件：i5-8400 6 核，8 GB RAM，1 TB HDD

3.1 Simulation Experiments

• RPVIO-Sim Dataset：在虚幻引擎中构建了一个具有动态物体的室内仓库环境。环境与 AirSim 集成，以生成四旋翼飞行器并收集视觉惯性数据。收集了 20 Hz 的单目 RGB 图像及其平面实例掩码，IMU 测量值和 1000 Hz 的真实姿态。IMU 测量值被次采样到 200hz。由记录过程的时间偏移使用 Kalibr 进行校准。

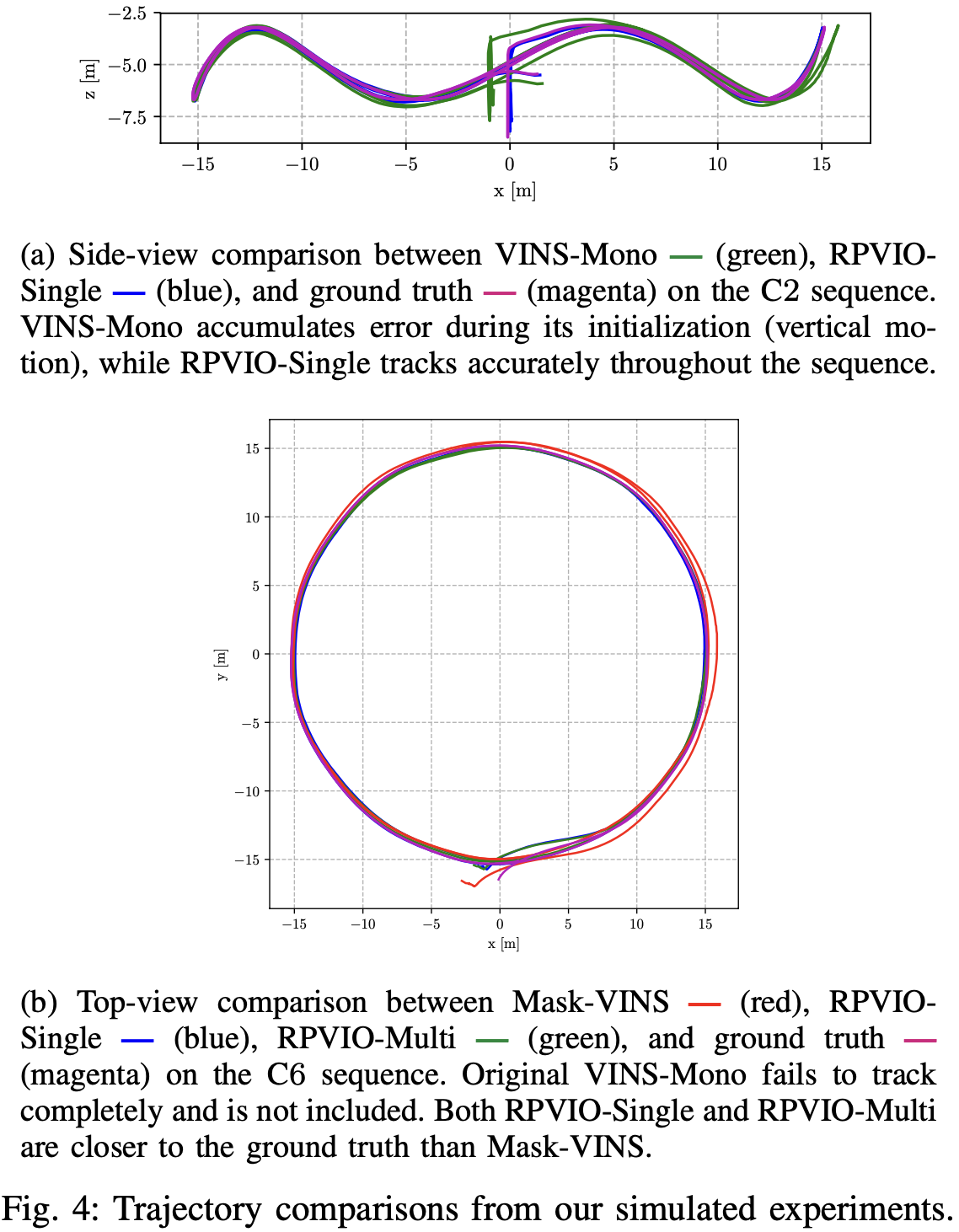
使用了方法的两个版本：RPVIO-Single 和 RPVIO-Multi。RPVIO- Single 在优化中只包含最大可见平面的特征，而 RPVIO- Multi 包含所有可见平面的特征。

还创建了另一个版本的 VINS-Mono，称为 Mask-VINS，经过修改以接受相同的平面实例掩码作为额外的输入。后端保持与VINS-Mono相同。

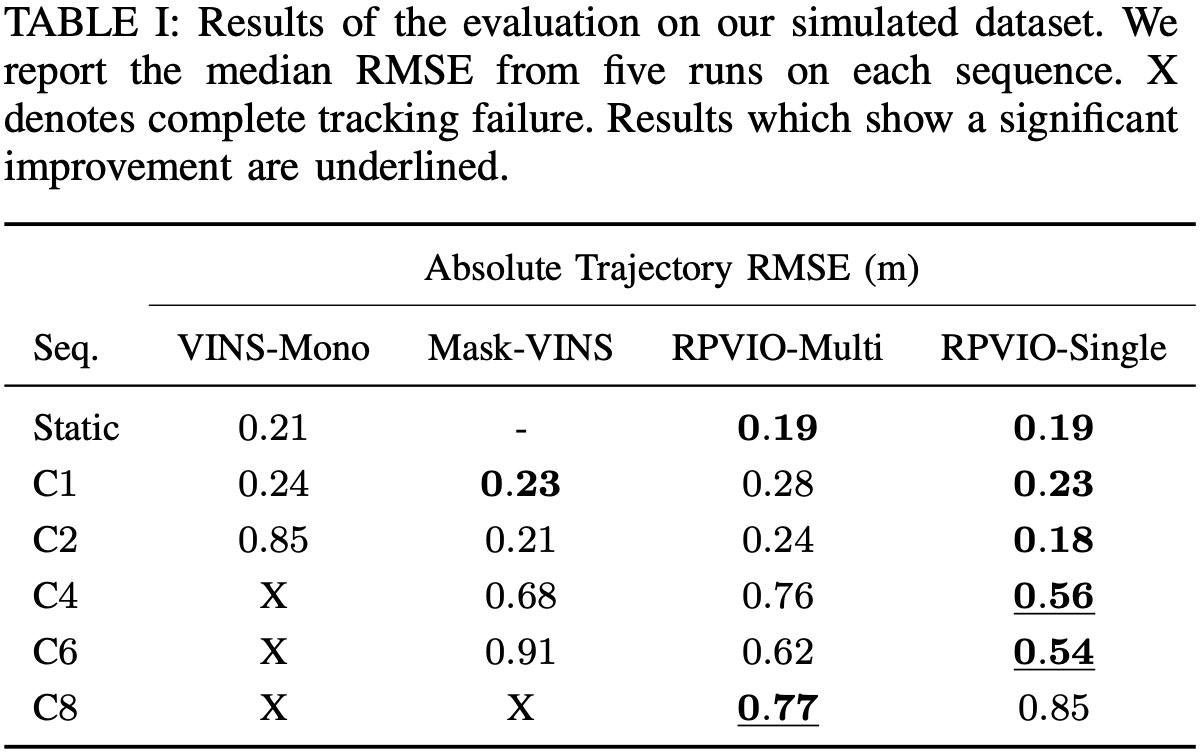
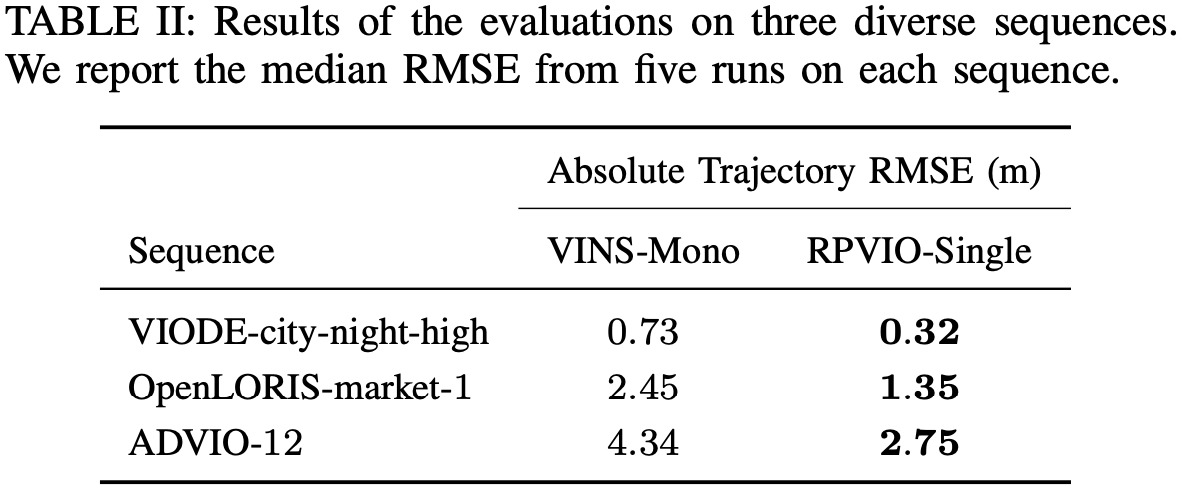
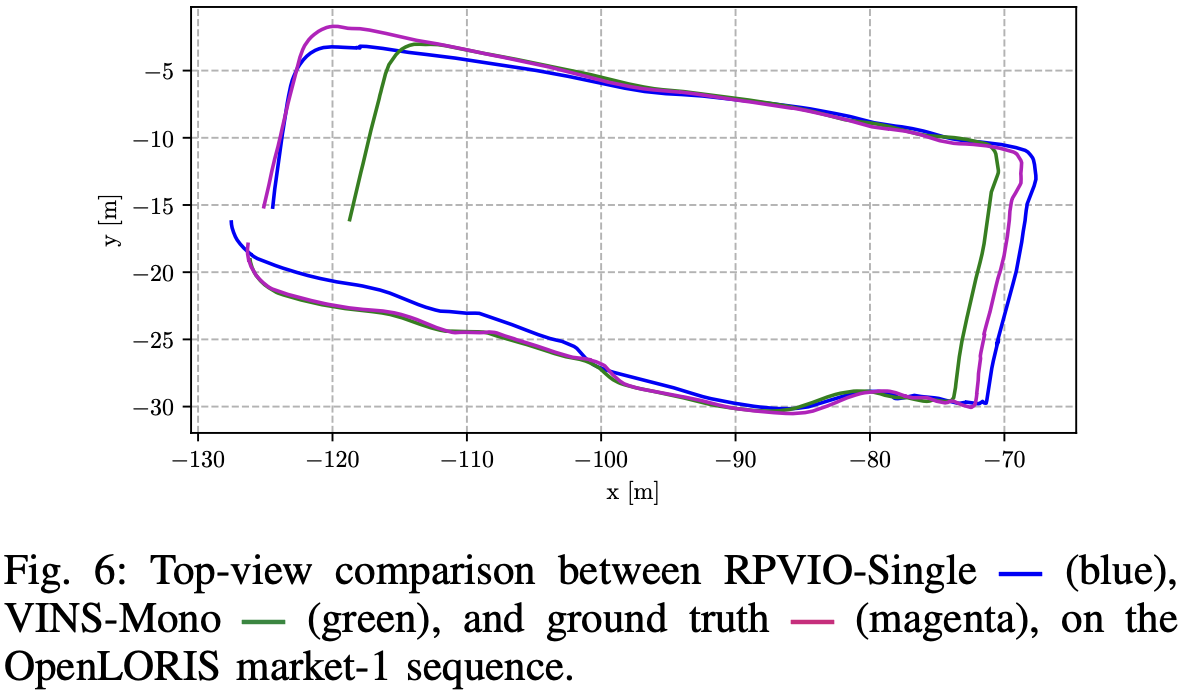
3.2 Experiments on Standard Datasets

参考文献

• [1] E. Malis and M. Vargas, “Deeper understanding of the homography decomposition for vision-based control,” INRIA, Tech. Rep. inria- 00174036, 2007.
• [2] T. Qin, P. Li, and S. Shen, “VINS-Mono: A robust and versatile monocular Visual-Inertial state estimator,” IEEE Trans. Rob., vol. 34, no. 4, pp. 1004–1020, Aug. 2018.
• [3] F. Yang and Z. Zhou, “Recovering 3d planes from a single image via convolutional neural networks,” in Proceedings of the European Conference on Computer Vision (ECCV), 2018, pp. 85–100.