Attention Mechanism

注意力机制在 Transformer 中很常见，目前也经常被用于计算机视觉当中。本文整理总结了网络上关于注意力机制的介绍。

注意力机制

---

1 Encoder-Decoder 框架

目前大多数注意力模型附着在 Encoder-Decoder 框架下。下图是 NLP 处理中常用的 Encoder-Decoder 框架：

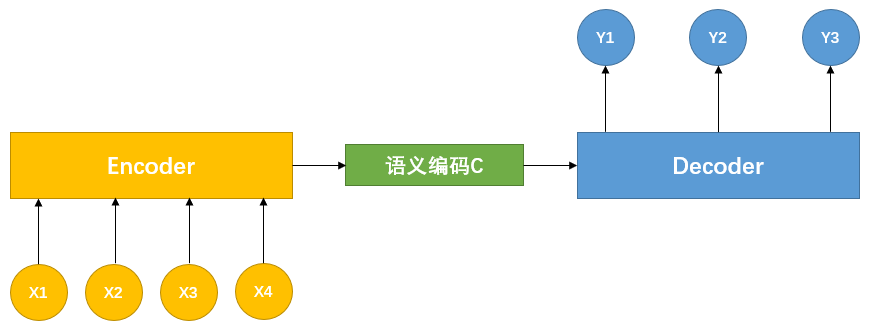
图-1 Encoder-Decoder 框架

可以简单理解为处理一个语句（篇章）生成另一个语句（篇章）的模型：对于句子 $<Source, Target>$，目标是输入句子 $Source$，期待通过 Encoder-Decoder 框架生成目标句子 $Target$，$Source$ 和 $Target$ 的单词序列为：

$Source=<x_1,x_2,...,x_m>\\ Target=<y_1,y_2,...,y_n>$

编码器 Encoder 通过对句子 $Source$ 进行编码，将输入的句子通过非线性变换转化为中间语义编码

$C=\mathcal{F}(x_1,x_2,...,x_m)$

解码器 Decoder 将中间语义编码 $C$ 和之前已经产生的历史输出单词序列 $y_1,y_2,...,y_{i-1}$ 来生成第 $i$ 步的单词

$y_i=\mathcal{G}(C,y_1,y_2,...,y_{i-1})$

若 $Source$ 和 $Target$ 是不同语言的句子，那么是机器翻译 Encoder-Decoder 框架；若 $Source$ 是一篇文章，而 $Target$ 是文章的概括性描述，那么是文本摘要 Encoder-Decoder 框架；若 $Source$ 是一句问句，而 $Target$ 是问句的回答，那么是问答系统或对话机器人 Encoder-Decoder 框架。

除 NLP 领域外，Encoder-Decoder 框架在其他领域也被广泛应用，如语音识别领域，Encoder 的输入是语音流，而 Decoder 的输出为语音所对应的文本；在 CV 领域，Encoder 的输入是一帧图片，Decoder 的输出是描述图片语义特征的描述语。通常 NLP 和语音识别时 Encoder 采用 RNN，而 CV 则采用 CNN。

2 经典 Attention 模型（Soft-Attention）

2.1 Attention 的引入

图-1 中的 Encoder-Decoder 框架没有体现出 “注意力机制”，因此可以将其看作注意力不集中的分心模型。为什么称其注意力不集中？先观察下面 $Target$ 中每个单词的生成过程：

$\begin{aligned} y_1 &= \mathcal{G}(C) \\ y_2 &= \mathcal{G}(C, y_1) \\ y_3 &= \mathcal{G}(C, y_1, y_2) \\ ... \end{aligned}$

式中 $\mathcal{G}$ 为 Decoder 的非线性变化函数。从上面的生成过程可以看出，不论生成哪一个单词，所使用的输入句子 $Source$ 的语义编码 $C$ 是相同的。需要注意的是 $C$ 由 $Sourc$ 的每个单词经 Encoder 编码生成，这也意味着，对于每一个 $Target$ 中的单词 $y_i$ 来说，输入句子 $Source$ 中的每一个单词对其生成都有着相同的影响力，因此称这个模型注意力不集中。

例：对于机器翻译，输入句子 “Tom chase Jerry”，Encoder-Decoder 逐步生成中文单词：“汤姆”、“追逐”、“杰瑞”。在翻译 “杰瑞” 时，分心模型里所有输入英文单词对目标单词 “杰瑞” 的影响是相同的，这显然不合理，因为 “Jerry” 翻译为 “杰瑞” 更加合理，而分心模型无法体现这一点。

不引入注意力机制，在输入短句子时可能没有明显的问题，但是对于长难句来说，输入句子的语义信息仅通过一个中间语义编码向量来表示，单词本身的信息大量丢失，极大影响输出结果的正确性，因此，这就是引入注意力机制的重要原因。

再用上面的翻译例子，引入 Attention 后，在翻译 “杰瑞” 时，将体现出不同英文单词对于翻译当前中文单词不同的影响程度，例如如下的概率分布：

$(\mathrm{Tom}, 0.3),\ (\mathrm{Chase}, 0.2),\ (\mathrm{Jerry}, 0.5)$

每个英文单词的概率表示翻译 “杰瑞” 时，注意力分配给不同英文单词的注意力大小，这引入了新的信息，将有助于正确翻译目标单词。

同理，$Target$ 中的每个单词都应学到其对应的 $Source$ 中单词的注意力概率分布。这也就意味着，在生成单词 $y_i$ 时，前面所使用的相同的中间语义编码 $C$ 被替换为根据当前生成单词而不断变化的 $C_i$ ，如下图所示：

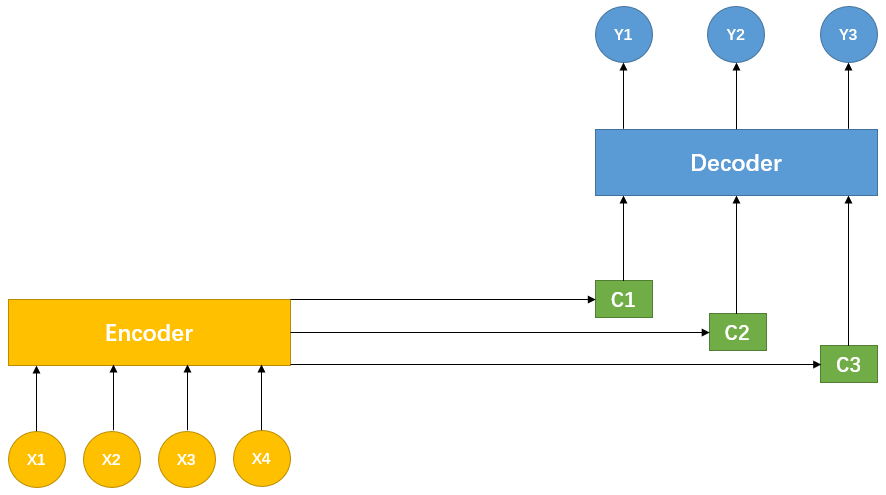
图-2 引入注意力机制的 Encoder-Decoder 框架

即生成 $Target$ 的过程变为：

$\begin{aligned} y_1 &= \mathcal{G}_1 (C_1) \\ y_2 &= \mathcal{G}_2 (C_2, y_1) \\ y_3 &= \mathcal{G}_3 (C_3, y_1, y_2) \end{aligned}$

每个 $C_i$ 可能对应不同的 $Source$ 中单词的注意力概率分布，以前面的翻译例子，其对应的信息可能如下：

$\begin{aligned} C_{\mathrm{汤姆}} &= \mathcal{g}(0.6*\mathcal{f}(\mathrm{Tom}),\ 0.2*\mathcal{f}(\mathrm{Chase}),\ 0.2*\mathcal{f}(\mathrm{Jerry})) \\ C_{\mathrm{追逐}} &= \mathcal{g}(0.2*\mathcal{f}(\mathrm{Tom}),\ 0.7*\mathcal{f}(\mathrm{Chase}),\ 0.1*\mathcal{f}(\mathrm{Jerry})) \\ C_{\mathrm{杰瑞}} &= \mathcal{g}(0.3*\mathcal{f}(\mathrm{Tom}),\ 0.2*\mathcal{f}(\mathrm{Chase}),\ 0.5*\mathcal{f}(\mathrm{Jerry})) \end{aligned}$

其中，$\mathcal{f}$ 表示 Encoder 对输入英文单词的某种变换函数，例如：如果 Encoder 使用 RNN 模型，那么 $\mathcal{f}$ 的函数结果往往是某时刻输入 $x_i$ 后隐藏节点的状态值；$\mathcal{g}$ 表示 Encoder 根据单词的中间编码合成整个句子中间语义编码的变换函数，一般，$\mathcal{g}$ 函数是对构成元素的加权求和，即下式：

$C_i = \sum_{j=1}^{L_x} a_{ij}h_j$

其中：$L_x$ 表示句子 $Source$ 的长度；$a_{ij}$ 表示在 $Target$ 输出第 $i$ 个单词时 $Source$ 句子中第 $j$ 个单词的注意力系数分配；$h_j$ 表示 $Source$ 句子中第 $j$ 个单词的语义编码。以前面的例子为例，则有 $L_x = 3$，$h_1 = \mathcal{f}(\mathrm{Tom})$，$h_2 = \mathcal{f}(\mathrm{Chase})$，$h_3 = \mathcal{f}(\mathrm{Jerry})$ 分别是 $Source$ 中每个单词的语义编码，对于编码 $C_1$ 而言，权重为 $a_{11} = 0.6$，$a_{12}=0.2$，$a_{13}=0.2$，其形成过程如下图：

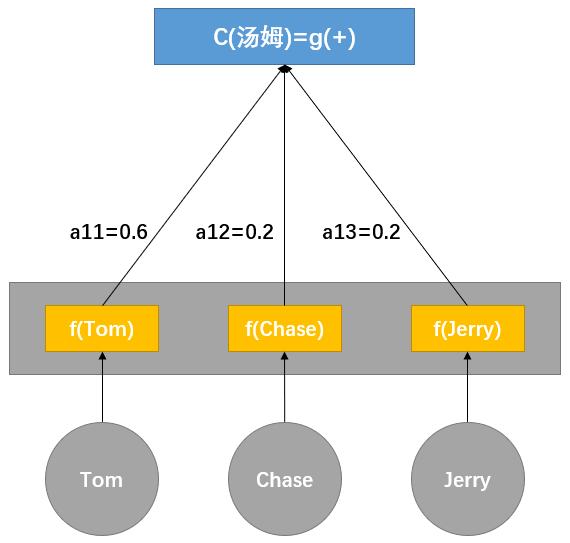
图-3 Attention 在翻译时的形成过程示意图

这个过程还存在一个问题，即在形成 Attention 时，如何得到 $Source$ 单词的注意力概率分布，例如翻译 “杰瑞” 时如何得到概率分布 $(\mathrm{Tom}, 0.3)$，$(\mathrm{Chase}, 0.2)$，$(\mathrm{Jerry}, 0.5)$？

2.2 Attention 中注意力分布的生成

先对图-1 中非 Attention 的 Encoder-Decoder 框架细化，Encoder 和 Decoder 采用 RNN 模型，得到下面的框架图：

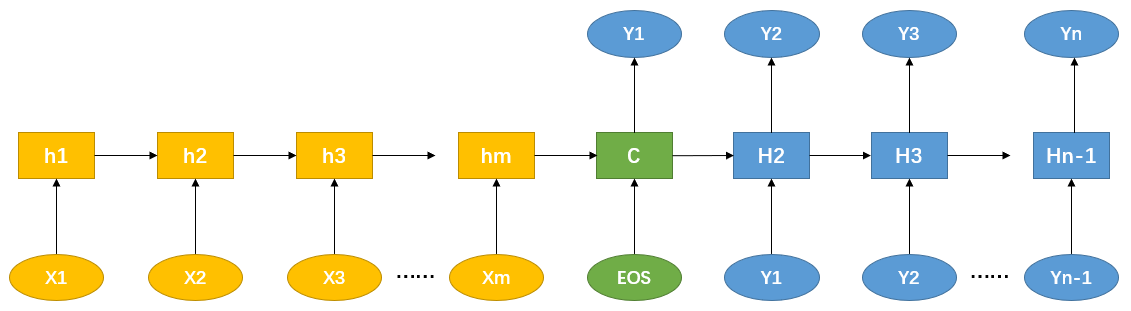
图-4 使用 RNN 细化后的 Encoder-Decoder 框架

用下图说明注意力概率分布的通用计算过程：

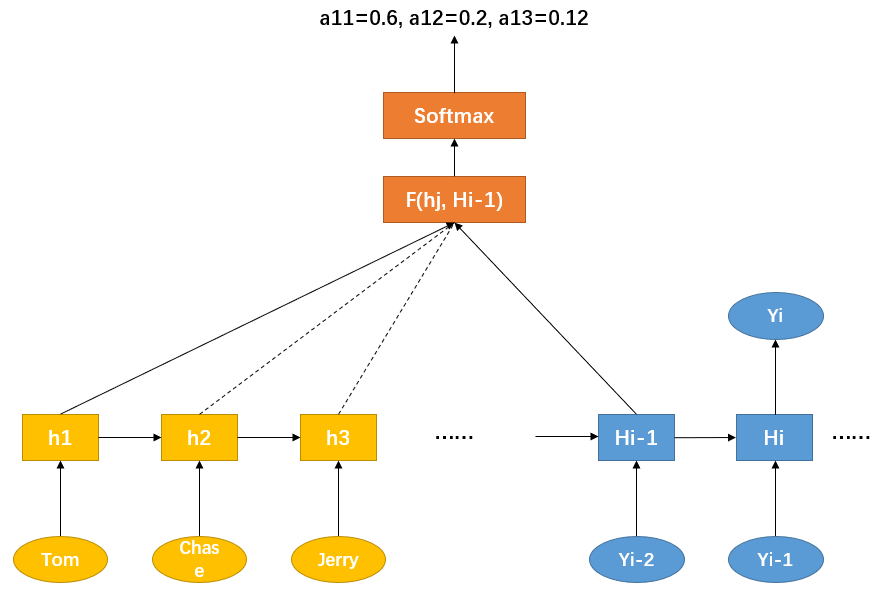
图-5 注意力概率分布的计算过程

对于使用 RNN 的 Decoder 而言，在时刻 $i$ 若要生成单词 $y_i$，由于可以得知时刻 $i-1$ 的隐藏层节点 $H_{i-1}$ 的值，那么可以把 $H_{i-1}$ 和 $Source$ 中每个单词对应的隐藏层节点 $h_j$ 分别计算，即通过函数 $F(h_j,H_{i-1})$ 获得目标单词 $y_i$ 和每个输入单词的对齐可能性（$F$ 在不同模型中使用的方法不同），然后函数 $F$ 的输出经过 Softmax 进行归一化后，即得到符合概率分布的注意力概率分布。图-6 中可视化的是英语-德语翻译系统加入 Attention 机制后，$Source$ 和 $Target$ 中单词对应的概率分布：

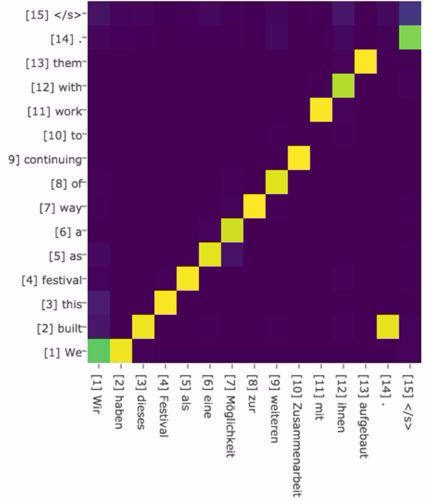
图-6 英语-德语翻译中 Attention 的概率分布

2.3 Attention 机制的本质

将 Attention 机制从 Encoder-Decoder 框架中剥离，并进一步抽象，可以更简单地看出 Attention 机制的本质。

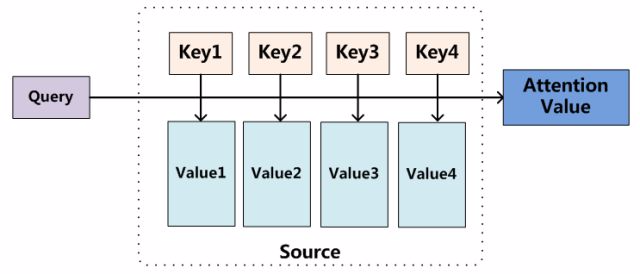
图-7 Attention 机制的本质思想

以图-7 为例：将 $Source$ 中的构成元素抽象为一些列的键值对数据 $<key, value>$，此时，对于给定 $Target$ 中的某个元素 $query$，通过计算 $query$ 和各个 $key$ 的相似性或相关性，得到每个 $key$ 对应 $value$ 的权重系数，然后对 $value$ 进行加权求和，即得到最终的 Attention 数值。因此本质上，Attention 机制是对 $Source$ 中元素的 $value$ 值进行加权求和，而 $query$ 和 $key$ 用来计算对应 $value$ 的权重系数。即可以将其本质思想改写为如下公式：

$\mathrm{Attention}(query, Source) = \sum_{i=1}^{L_x} \mathrm{Similarity}(query, key_i) * value_i$

其中，$L_x=||Source||$。在前面机器翻译的例子里计算 Attention 的过程中，$Source$ 中的 $key$ 和 $value$ 指向的则是同一个数据，即输入句子中单词的语义编码。

从图-7 可以引出另外一种理解，将 Attention 机制看作一种软寻址（Soft Addressing）：$Source$ 可以看作存储器内存储的内容，元素由地址 $key$ 和值 $value$ 组成，当前有个 $key=query$ 的查询，目的是取出存储器中对应的 $value$ 值，即 Attention 数值。通过 $query$ 和存储器内元素的地址 $key$ 进行相似性比较寻址。之所以成为软寻址，指的不同一般寻址从存储中找出取出一条数据，而是可能从每个 $key$ 地址都会取出内容，取出内容的重要性根据 $query$ 和 $key$ 的相似性决定，之后对 $value$ 进行加权求和，从而得到最终的 $value$ 值，即 Attention 值。

对于 Attention 机制的具体计算过程，对目前大多数方法进行抽象，可以归纳为两个过程三个阶段：

• 过程 1：根据 $query$ 和 $key$ 计算权重系数

  • 阶段①：根据 $query$ 和 $key$ 计算两者的相似性或相关性
  • 阶段②：对阶段①的原始分值进行归一化处理

• 过程 2（阶段③）：根据权重系数对 $value$ 进行加权求和

上面的过程可以得到图-8 中的结果：

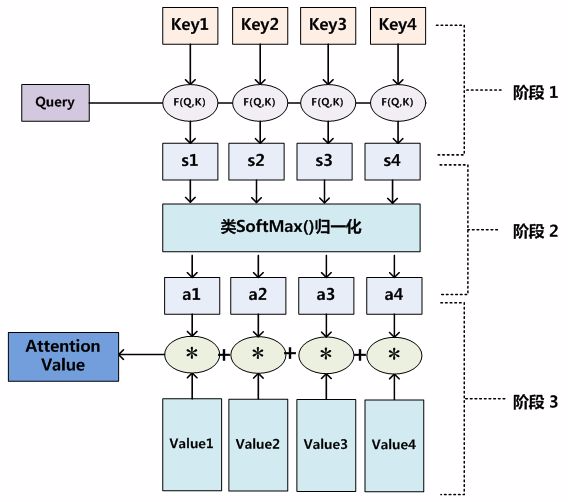
图-8 计算 Attention 的三个阶段

在阶段①，可以使用不同的函数和计算方法，根据 $query(=q)$ 和 $key_i(=k_i)$，计算两者的相似性或相关性，常见的方法如下（式中 $W$、$U$ 和 $v$ 为可学习的参数矩阵或向量，$D$ 为输入向量的维度）：

• 点积

  $s_i = \mathrm{Similarity}(query, key_i) = query \cdot key_i = q^T k_i$

• 缩放点积

  $s_i = \mathrm{Similarity}(query, key_i) = \frac{q^T k_i}{\sqrt{D}}$

• 余弦（cosine）相似性

  $s_i = \mathrm{Similarity}(query, key_i) = \frac{query \cdot key_i}{||query|| \cdot ||key_i||}$

• MLP 网络：$s_i = \mathrm{Similarity}(query, key_i) = \mathrm{MLP}(query, key_i)$

  • 加性模型：$s_i = \mathrm{Similarity}(query, key_i) = v^T \tanh (Wk_i+Uq)$
  • 双线性模型：$s_i = \mathrm{Similarity}(query, key_i) = k_i^T W q$，可以重塑为 $s_i = \mathrm{Similarity}(query, key_i) = k_i^T (U^T V) q = (U k_i)^T (Vq)$，即对 $query$ 和 $key$ 进行线性变换后，再计算点积。

阶段②引入类似 Softmax 的计算，对阶段①的结果一方面进行归一化，另一方面也突出重要元素的权重：

$a_i = \mathrm{Softmax}(s_i) = \frac{\exp(s_i)}{\sum_{j=1}^{L_x}\exp(s_j)}$

然后加权得到 Attention 值：

$\mathrm{Attention}(query, Source) = \sum_{i=1}^{L_x} a_i \cdot value_i$

目前大多数的注意力机制都符合上述的三阶段的计算过程。

3 Attention 注意力机制的变体

3.1 硬性注意力（Hard Attention）

软性注意力通过注意力分布加权求和来融合输入向量。而硬性注意力则不采用这种方式，它根据注意力分布选择输入向量中的一个作为输出：

$\mathrm{Attention}(query, Source) = value_{i*} \\ \mathrm{where}\ i* = \mathrm{ArgCondition}(a_i\ \mathrm{or}\ s_i) \\ i*\ 即满足\ \mathrm{Condition}\ 条件的\ a_i\ 或\ s_i\ 的索引$

这种选择有两种选择方式：

• 选择注意力分布中，分数（概率）最大的一项所对应的输入向量作为 Attention 的输出。
• 根据注意力分布进行随机采样，采样结果作为 Attention 的输出。

硬性注意力通过上面的方式选择 Attention 的输出，会使最终的损失函数与注意力分布之间的函数关系不可导，从而无法使用反向传播算法训练模型，硬性注意力通常需要使用强化学习来进行训练。一般深度学习算法会使用软性注意力的方式进行计算。

3.2 多头注意力（Multi-Head Attention）

多头注意力机制是利用多个查询向量 $Q = [q_1, q_2, ... , q_m]$，并行地从输入信息 $<key, value>$ 或 $(K,V)=[(k_1,v_1),(k_2,v_2),...,(k_n,v_n)]$ 中选取多组信息。在查询过程中，每个查询向量 $q_i$ 将会关注输入信息的不同部分。

假设 $a_{ij}$ 表示第 $i$ 个查询向量 $q_i$ 与第 $j$ 个输入信息 $k_j$ 的注意力权重，$s(\cdot)=\mathrm{Similarity}(\cdot)$，$context_i$ 表示由查询向量 $q_i$ 计算得出的 Attention 输出向量，其计算方式为：

$a_{ij} = \mathrm{Softmax}(s(q_i,k_j)) = \frac{\exp(s(q_i,k_j))}{\sum_{t=1}^n \exp(s(q_i,k_t))} \\ context_i = \sum_{j=1}^n a_{ij} \cdot v_j$

最终将所有查询向量的计算结果进行拼接得到最终结果（$\oplus$ 表示向量拼接操作）：

$\mathrm{Attention} = context_1 \oplus context_2 \oplus \cdots \oplus context_m$

4 自注意力机制（Self-Attention）

Self-Attention 也被称为 Intra-Attention（内部 Attention）。在一般 Encoder-Decoder 框架中，输入 $Source$ 和输出 $Target$ 内容是不相同的，Attention 机制发生在 $Target$ 的元素 $query$ 和 $Source$ 中的所有元素之间。Self-Attention 不是 $Target$ 和 $Source$ 之间的 Attention 机制，而是 $Source$ 内部元素之间或者 $Target$ 内部元素之间发生的 Attention 机制，也可以理解为 $Target=Source$ 这种特殊情况下的注意力计算机制。

在前面所介绍的 Attention 机制中，会使用一个查询向量 $q$ 和对应的输入 $H=[h_1,h_2,...,h_n]$ 进行计算，查询向量 $q$ 则和任务相关，例如 Encoder-Decoder 框架中，$q$ 可以是 Decoder 端前一时刻的输出状态向量。而在 Self-Attention 中，查询向量也可以使用输入信息生成，而非任务相关的向量。即模型读到输入信息后，根据输入信息本身决定当前的重要信息。

自注意力机制往往采用 Query-Key-Value 的模式，以 BERT 重点自注意力机制为例，展开下面的讨论，如图-9 所示：

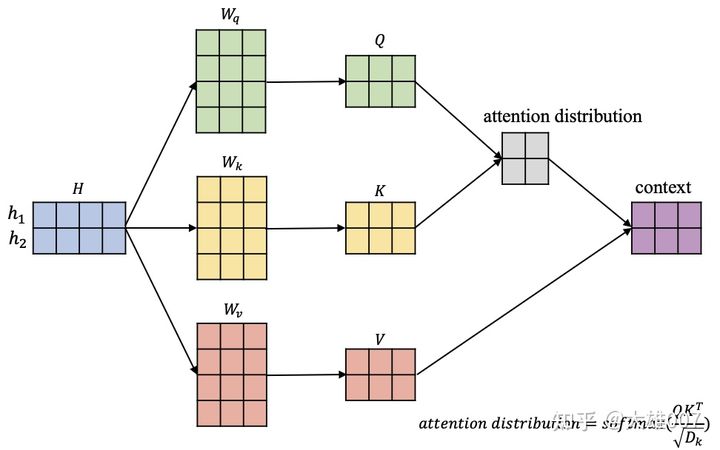
图-9 自注意力机制的计算过程

图-9 中，输入信息 $H=[h_1,h_2]$，蓝色矩阵中每行表示一个输入向量，三个矩阵 $W_q$，$W_k$，$W_v$ 将输入信息 $H$ 以此转换到对应的查询空间 $Q=[q_1,q_2]$，键空间 $K=[k_1,k_2]$ 和值空间 $V=[v_1,v_2]$：

$\begin{aligned} Q &= [q_1=h_1 W_q,\ q_2=h_2 W_q] &\Rightarrow Q = HW_q \\ K &= [k_1=h_1 W_k,\ k_2=h_2 W_k] &\Rightarrow K = HW_k \\ V &= [v_1=h_1 W_v,\ v_2=h_2 W_v] &\Rightarrow V = HW_v \end{aligned}$

不妨以 $h_1$ 为例计算这个位置的 Attention 输出向量 $context_1$，如图-10 所示，其中 $D_k$ 表示 $key$ 向量的维度（$query$ 向量、$key$ 向量和 $value$ 向量的维度相同）：

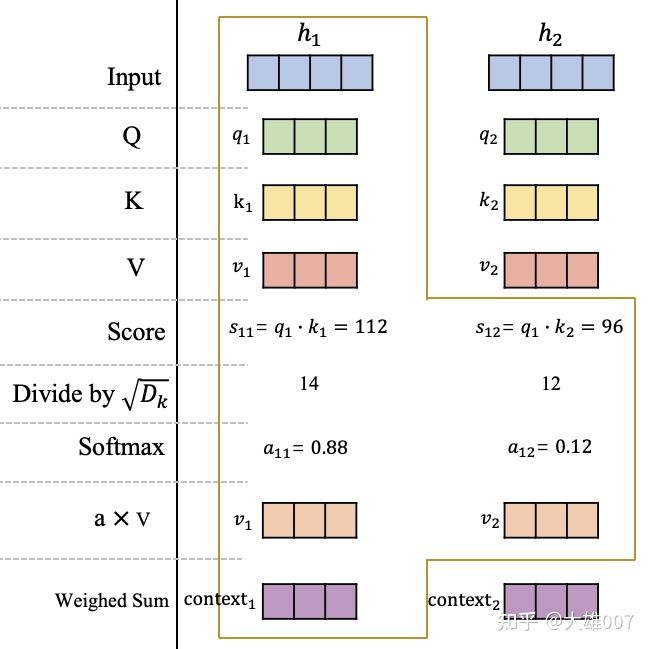
图-10 自注意力机制的详细计算过程

在获得输入信息 $H$ 在不同空间的表达 $Q$、$K$ 和 $V$ 后，计算 $q_1$ 在 $h_1$ 和 $h_2$ 的分数（相似性或相关性） $s_{11}$ 和 $s_{12}$。然后用 Softmax 进行归一化，获得在 $h_1$ 这个位置的注意力分布 $a_{11}$ 和 $a_{12}$，代表了模型当前在 $h_1$ 这个位置需要对输入信息 $h_1$ 和 $h_2$ 的关注程度。最后，根据该位置的注意力分布对 $v_1$ 和 $v_2$ 进行加权平均获得 $h_1$ 位置的 Attention 向量 $context_1$。

同理，对于输入信息 $H=[h_1,h_2,...,h_n]$，可以得到每个位置的 Attention 向量 $\mathrm{Attention}=[context_1,context_2,...,context_n]$。

整个 Self-Attention 的计算过程的矩阵形式为：

$\mathrm{Attention} = \mathrm{Softmax} (\frac{QK^T}{\sqrt{D_k}})V$

参考

• https://www.cnblogs.com/jins-note/p/13056604.html
• https://zhuanlan.zhihu.com/p/393940472