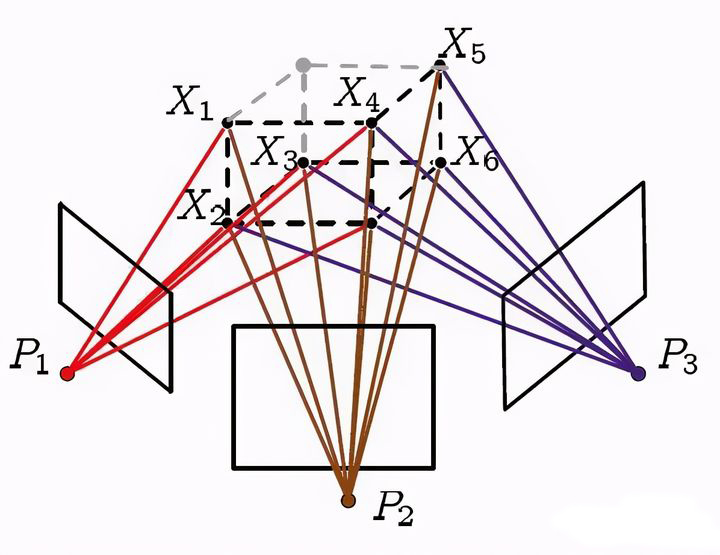
Bundle Adjustment

Posted on 2022-08-09 Edited on 2022-11-18 In Summary Waline:

Bundle Adjustment（光束平差法、捆集调整等）是指从视觉重建中计算出最优的 3D 模型和相机参数（内参和外参）。从每个特征点反射出来的几束光线（bundles of light rays），在把相机姿态和特征点的位置做出最优的调整（adjustment）之后，最后收束到光心的这个过程，简称 BA。

本文总结网络资源，对 BA 进行了总结。

Bundle Adjustment

1 介绍

图-1 BA 示意

2 原理

假设空间位置的 3D 点为： $X = \{ x_1, x_2, ..., x_n \}$ ，相机中心位姿为 $P =\{ p_1, p_2, ..., p_m \}$ 。 $u_i$ 为 $x_i$ 对应的像素位置， $K$ 为相机的内参矩阵， $s_i$ 为 $u_i$ 对应的深度值。如图，BA 要计算的误差是观测值和估计值之间的误差。

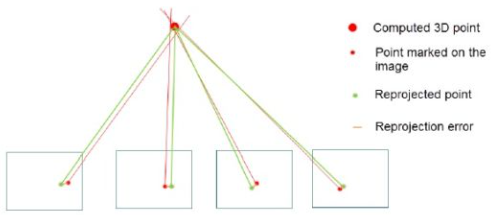
图-2 BA 的计算目标

对于单个相机的 BA，可以构建重投影误差最小二乘如下：

$\varepsilon (X, T) = \sum_{i=1}^{n} || u_i - \frac{1}{s_i} K T x_i ||^2$

其中，变换矩阵 $T$ 满足约束：

$T = \left[ \begin{matrix} R &t \\ \pmb{0}^T &1 \end{matrix} \right] \in SE(3),\ R^T R = I, \ det(R) = 1,\ t \in \mathbb{R}^3$

对于有约束的变换矩阵在最小二乘中不便求解，因此转换为无约束的李群求解：

$\varepsilon (X, T) = \sum_{i=1}^{n} || u_i - \frac{1}{s_i} K \cdot \exp (\xi^{\wedge}) \cdot x_i ||^2$

定义误差函数为：

$f (x_i, \xi) = u_i - K \cdot \exp (\xi^{\wedge}) \cdot x_i$

对于高斯牛顿法，函数 $f(x)$ 有增量方程：

$J(x)^T \cdot J(x) \cdot \Delta x = -J(x)^T \cdot f(x)$

仅需要求 $f(x_i, \xi)$ 的一阶导（Jacobian 矩阵）。

3 C++ 代码

优化相机内参及畸变系数，相机的位姿（6dof）和 landmark 代价函数写法如下：

template <typename CameraModel>
class BundleAdjustmentCostFunction {
public:
  explicit BundleAdjustmentCostFunction(const Eigen::Vector2d& point2D)
      :observed_x_(point2D(0)), observed_y_(point2D(1)) {}
  // 构造函数传入的是观测值
  static ceres::CostFunction* Create(const Eigen::Vector2d& point2D) {
    return (new ceres::AutoDiffCostFunction<
            BundleAdjustmentCostFunction<CameraModel>, 2, 4, 3, 3,
            CameraModel::kNumParams>(new BundleAdjustmentCostFunction(point2D)));
  }
  // 优化量:2代表误差方程个数;4代表pose中的姿态信息,用四元数表示;3代表pose中的位置信息;3代表landmark自由度;CameraModel::kNumParams是相机内参和畸变系数,其取决于相机模型


  // opertator 重载函数的参数即是待优化的量
  template <typename T>
  bool operator()(const T* const qvec, const T* const tvec,
                  const T* const point3D, const T* const camera_params,
                  T* residuals) const {
    // Rotate and translate.
    T projection[3];
    ceres::UnitQuaternionRotatePoint(qvec, point3D, projection);
    projection[0] += tvec[0];
    projection[1] += tvec[1];
    projection[2] += tvec[2];

    // Project to image plane.
    projection[0] /= projection[2];
    projection[1] /= projection[2];

    // Distort and transform to pixel space.
    CameraModel::WorldToImage(camera_params, projection[0], projection[1],
                              &residuals[0], &residuals[1]);

    // Re-projection error.
    residuals[0] -= T(observed_x_);
    residuals[1] -= T(observed_y_);

    return true;
  }

private:
  const double observed_x_;
  const double observed_y_;
};

ceres 自动求导，代码如下：

ceres::Problem problem;
ceres::CostFunction* cost_function = nullptr; 
ceres::LossFunction * p_LossFunction =
    ceres_options_.bUse_loss_function_ ?
      new ceres::HuberLoss(Square(4.0))
      : nullptr; // 关于为何使用损失函数,因为现实中并不是所有观测过程中的噪声都服从 
      // gaussian noise的（或者可以说几乎没有），
      // 遇到有outlier的情况，这些方法非常容易挂掉，
      // 这时候就得用到robust statistics里面的
      // robust cost(*cost也可以叫做loss, 统计学那边喜欢叫risk) function了，
      // 比较常用的有huber, cauchy等等。
cost_function = BundleAdjustmentCostFunction<CameraModel>::Create(point2D.XY()); 
// 将优化量加入残差块
problem_->AddResidualBlock(cost_function, p_LossFunction, qvec_data,
                                 tvec_data, point3D.XYZ().data(),
                                 camera_params_data);

优化相机内参及畸变系数，pose subset parameterization（pose 信息部分参数优化）和 3D landmark，当只优化姿态信息时，problem 需要添加的代码如下：

map_poses[indexPose] = {angleAxis[0], angleAxis[1], angleAxis[2], t(0), t(1), t(2)};

double * parameter_block = &map_poses.at(indexPose)[0];
problem.AddParameterBlock(parameter_block, 6);
std::vector<int> vec_constant_extrinsic;
vec_constant_extrinsic.insert(vec_constant_extrinsic.end(), {3,4,5});
if (!vec_constant_extrinsic.empty()) {
    // 主要用到ceres的SubsetParameterization函数
    ceres::SubsetParameterization *subset_parameterization =
        new ceres::SubsetParameterization(6, vec_constant_extrinsic);
    problem.SetParameterization(parameter_block, subset_parameterization);
}

优化相机内参及畸变系数，pose subset parameterization（pose 信息部分参数优化）和 3D landmark，当只优化位置信息时，problem 需要添加的代码如下（同上，只需修改一行）：

map_poses[indexPose] = {angleAxis[0], angleAxis[1], angleAxis[2], t(0), t(1), t(2)};

double * parameter_block = &map_poses.at(indexPose)[0];
problem.AddParameterBlock(parameter_block, 6);
std::vector<int> vec_constant_extrinsic;
vec_constant_extrinsic.insert(vec_constant_extrinsic.end(), {1,2,3});
if (!vec_constant_extrinsic.empty()) {
    ceres::SubsetParameterization *subset_parameterization =
        new ceres::SubsetParameterization(6, vec_constant_extrinsic);
    problem.SetParameterization(parameter_block, subset_parameterization);
}

优化相机内参及畸变系数，pose 是常量不优化和 3D landmark，代价函数写法如下：

// 相机模型
template <typename CameraModel>  
class BundleAdjustmentConstantPoseCostFunction {
public:
  BundleAdjustmentConstantPoseCostFunction(const Eigen::Vector4d& qvec,
                                           const Eigen::Vector3d& tvec,
                                           const Eigen::Vector2d& point2D)
      : qw_(qvec(0)),
        qx_(qvec(1)),
        qy_(qvec(2)),
        qz_(qvec(3)),
        tx_(tvec(0)),
        ty_(tvec(1)),
        tz_(tvec(2)),
        observed_x_(point2D(0)),
        observed_y_(point2D(1)) {}

  static ceres::CostFunction* Create(const Eigen::Vector4d& qvec,
                                     const Eigen::Vector3d& tvec,
                                     const Eigen::Vector2d& point2D) {
    return (new ceres::AutoDiffCostFunction<
            BundleAdjustmentConstantPoseCostFunction<CameraModel>, 2, 3,
            CameraModel::kNumParams>(
        new BundleAdjustmentConstantPoseCostFunction(qvec, tvec, point2D)));
  }

  template <typename T>
  bool operator()(const T* const point3D, const T* const camera_params,
                  T* residuals) const {
    const T qvec[4] = {T(qw_), T(qx_), T(qy_), T(qz_)};

    // Rotate and translate.
    T projection[3];
    ceres::UnitQuaternionRotatePoint(qvec, point3D, projection);
    projection[0] += T(tx_);
    projection[1] += T(ty_);
    projection[2] += T(tz_);

    // Project to image plane.
    projection[0] /= projection[2];
    projection[1] /= projection[2];

    // Distort and transform to pixel space.
    CameraModel::WorldToImage(camera_params, projection[0], projection[1],
                              &residuals[0], &residuals[1]);

    // Re-projection error.
    residuals[0] -= T(observed_x_);
    residuals[1] -= T(observed_y_);

    return true;
  }

private:
  const double qw_;
  const double qx_;
  const double qy_;
  const double qz_;
  const double tx_;
  const double ty_;
  const double tz_;
  const double observed_x_;
  const double observed_y_;
};

接下来 problem 加入残差块代码如下:

ceres::Problem problem;
ceres::CostFunction* cost_function = nullptr; 
ceres::LossFunction * p_LossFunction =
    ceres_options_.bUse_loss_function_ ?
      new ceres::HuberLoss(Square(4.0))
      : nullptr; // 关于为何使用损失函数,因为现实中并不是所有观测过程中的噪声都服从 
      // gaussian noise的（或者可以说几乎没有），
      // 遇到有outlier的情况，这些方法非常容易挂掉，
      // 这时候就得用到robust statistics里面的
      // robust cost(*cost也可以叫做loss, 统计学那边喜欢叫risk) function了，
      // 比较常用的有huber, cauchy等等。
cost_function = BundleAdjustmentConstantPoseCostFunction<CameraModel>::Create(
            image.Qvec(), image.Tvec(), point2D.XY()); // 观测值输入  
// 将优化量加入残差块
problem_->AddResidualBlock(cost_function, loss_function,
                           point3D.XYZ().data(), camera_params_data); // 被优化量加入残差-3D点和相机内参

1 介绍

2 原理

3 C++ 代码

参考