CLINS

在一个实数向量空间 $\mathcal{V}$ 中，对于给定集合 $X$，所有包含 $X$ 的凸集的交集 $S$ 被称为 $X$ 的凸包。$X$ 的凸包可以用 $X$ 内所有点 $(x_1,x_2,...,x_n)$ 的线性组合来构造。在二维欧氏空间中，凸包可以想象为一条刚好包括所有点的橡皮圈。

以不严谨的语言来描述，给定二维平面上的点集，凸包就是将最外层的点连接起来构成的凸多边形，它能包含点集中的所有点。如图-1，假设平面共有 $p_0 \sim p_{12}$ 共 13 个点，过某些点作一个多边形，使这个多边形能把所有点都“包”起来。当这个多边形是凸多边形的时候，就叫它“凸包”。

凸包算法

1 概念

在一个实数向量空间 $\mathcal{V}$ 中，对于给定集合 $X$，所有包含 $X$ 的凸集的交集 $S$ 被称为 $X$ 的凸包。$X$ 的凸包可以用 $X$ 内所有点 $(x_1,x_2,...,x_n)$ 的线性组合来构造。在二维欧氏空间中，凸包可以想象为一条刚好包括所有点的橡皮圈。

以不严谨的语言来描述，给定二维平面上的点集，凸包就是将最外层的点连接起来构成的凸多边形，它能包含点集中的所有点。如图-1，假设平面共有 $p_0 \sim p_{12}$ 共 13 个点，过某些点作一个多边形，使这个多边形能把所有点都“包”起来。当这个多边形是凸多边形的时候，就叫它“凸包”。

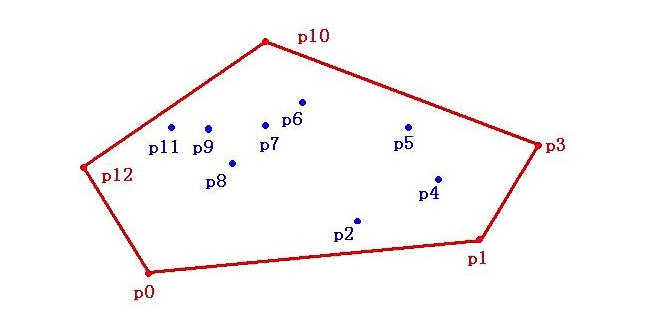
图-1 凸包示意

2 解法一（Graham 扫描法）

• 时间复杂度：$O(n\log n)$

2.1 计算步骤

Graham 扫描的思想是先找到凸包上的一个点，然后从那个点开始按逆时针方向逐个找凸包上的点，实际上就是进行极角排序，然后对其查询使用。 以图-2 为例，Graham 扫描法计算步骤为：

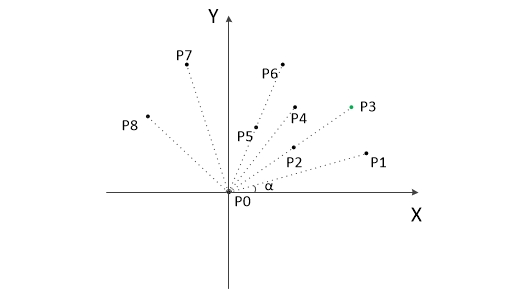
图-2 Graham扫描初始图

1. 把所有点放在二维坐标系中，则纵坐标最小的点一定是凸包上的点，如图-2 中 $P_0$。
2. 将所有点的坐标平移，使 $P_0$ 作为原点。
3. 计算各个点相对于 $P_0$ 的幅角 $\alpha$ ，按从小到大的顺序对各个点排序。当 $\alpha$ 相同时，距离 $P_0$ 比较近的排在前面。如图-2 得到的结果为 $P_1,P_2,P_3,P_4,P_5,P_6,P_7,P_8$。由几何知识可以知道，结果中第一个点 $P_1$ 和最后一个点 $P_8$ 一定是凸包上的点。以上，已经知道了凸包上的第一个点 $P_0$ 和第二个点 $P_1$，把它们放在栈 $S$ 里。把 $P_2$ 压入栈 $S$，假设 $S$ 的栈底元素为 $S[0]$，栈顶元素为 $S[t]$。
4. 对 $i$ 遍历 3 到 8（所有点的最大下标）：
5. 连接 $S[t-1]$ 和 $S[t]$ 得向量 $v_1$，连接 $S[t-1]$ 和 $P_i$ 得向量 $v_2$。
6. 若 $v_2$ 的方向相对于 $v_1$ 为左转，则把 $P_i$ 压入 $S$，继续步骤 4，否则进入步骤 7。
7. $S[t]$ 不满足凸包要求，把 $S[t]$ 弹出，继续步骤 5。

最后，栈中的元素就是凸包上的点。计算的动态过程如图-3。

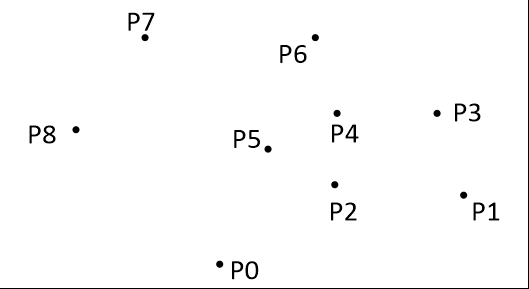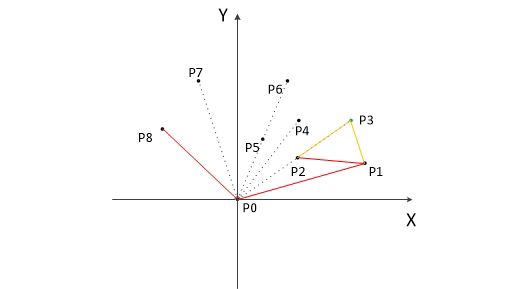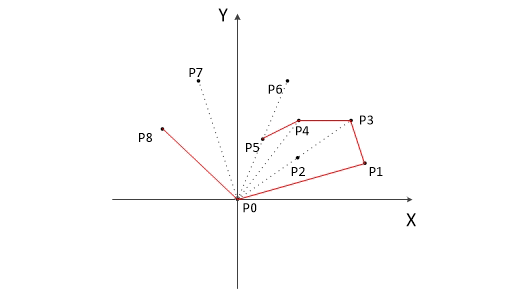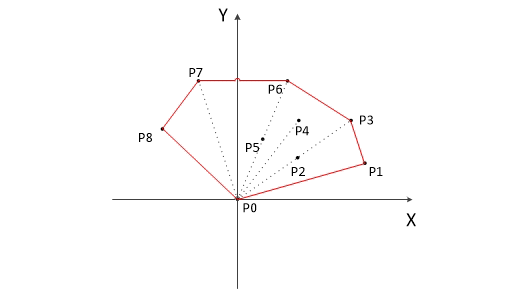
图-3 Graham扫描法计算过程

2.2 算法

图-4 Graham扫描法算法

2.3 CPP 代码

#include <iostream>
#include <vector>
#include <cmath>
 
using namespace std;

class mpoint {
//class point(x, y)
public:
    double x;
    double y;
    mpoint(double xx = 0, double yy = 0) {
        x = xx;
        y = yy;
    }
 
};
 
int get_miny_point_id(mpoint *points, int size) {
    //get the point with min_y
    int min_id = 0;
    double miny = 10000;
    for (int i = 0; i < size; i++) {
        if (points[i].y < miny) {
            miny = points[i].y;
            min_id = i;
        }
    }
    return min_id;
}
 
void get_cos(mpoint *points, double *mcos, int id, int size) {  
    //get point's cos
    double coss;
    for (int i = 0; i < size; i++) {
        if (i == id) {
            mcos[i] = 2;
        } else {
            coss = (points[i].x - points[id].x) / sqrt((points[i].x - points[id].x) * (points[i].x - points[id].x) + (points[i].y - points[id].y) * (points[i].y - points[id].y));
            mcos[i] = coss;
        }
    }
}
 
void sort_points(mpoint *points, double *mcos, int size) {   
    //sort the points
    int i, j;
    double temp_cos;
    mpoint temp_point;
    for (i = 0; i < size; i++) {
        for (j = 0; j < size - i - 1; j++) {      
            //bubble sorting
            if (mcos[j] < mcos[j + 1]) {
                temp_cos = mcos[j];
                mcos[j] = mcos[j + 1];
                mcos[j + 1] = temp_cos;
                
                temp_point = points[j];
                points[j] = points[j + 1];
                points[j + 1] = temp_point;
            }
        }
    }
}
 
int ccw(mpoint a, mpoint b, mpoint c) {          
    //judge if it is couter-colockwise
    double area = (b.x-a.x) * (c.y-a.y) - (b.y-a.y) * (c.x-a.x);
    if (area < 0) {
        return -1; // clockwise
    } else {
        if (area > 0) return 1; // counter-clockwise
        else return 0; // collinear
    }
    
}
 
void get_outpoint(mpoint *points, int size) {    
    //get points in stack
    vector<mpoint> outpoint;
    outpoint.push_back(points[0]);
    outpoint.push_back(points[1]);
    int i = 2;
    while (i != size) {
        if (ccw(outpoint[outpoint.size() - 2], outpoint[outpoint.size() - 1], points[i]) > 0) {
            outpoint.push_back(points[i]);
            i = i + 1;
        } else {
            outpoint.pop_back();
        }
    }
    cout << "The outpoints are: " << endl;
    for (int k = 0; k < outpoint.size(); k++) {
        cout << outpoint[k].x << " " << outpoint[k].y << endl;
    }
}
 
int main() {
    int size = 4;
    double px, py;
    cout << "Please input the size: ";
    cin >> size;
    mpoint *points;
    int miny_point_id;
    double *mcos;
    points = new mpoint[size];
    mcos = new double[size];
    for (int i = 0; i < size; i++) {
        cin >> px;
        cin >> py;
        points[i].x = px;
        points[i].y = py;
    }
    miny_point_id = get_miny_point_id(points, size);
    get_cos(points, mcos, miny_point_id, size);
    sort_points(points, mcos, size);
    get_outpoint(points, size);
}

2.4 左转的判断

对于前面的 $v_2$ 相对 $v_1$ 是左转还是右转，计算方式可以使用叉乘：

$v_1 \times v_2 = \left[ \begin{matrix} x_1 &x_2 \\ y_1 &y_2 \end{matrix} \right] =x_1 y_2 - x_2 y_1$

若值为正，则 $v_1$ 在 $v_2$ 的右侧（顺时针方向），若为负则 $v_1$ 在 $v_2$ 的左侧（逆时针方向）。

3 解法二（Javis-March 算法或 Gift Wrapping 算法）

• 时间复杂度：$O(NM)$，$N$ 为点的数量，$M$ 为凸包的顶点数。

3.1 计算步骤

1. 先确定凸包边界上的点 $p_1$ 和与下一个点 $p_2$（可以利用 Graham 扫描法中的方法）；
2. 在点集里去寻找下一个点 $p_3$，使得 $p_1,p_3,p_2$ 满足 CCW（Counterclockwise，以逆时针方向旋转）；
3. 如果满足，这就说明 $p_3$ 是更外围的点，把 $p_3$ 的值覆盖 $p_2$，即 $p_2 = p_3$；
4. 重复第 3 步，直到所有点都访问过，即为找到了下一个最外边的点；
5. 将 $p_2$ 的值覆盖 $p_1$，即 $p_1 = p_2$；
6. 重复第 2 步，直到下一个点回到起点。

3.2 CPP 代码

typedef vector<pair<double, double>> vpdd;
typedef pair<double, double> pdd;

bool ccw(pdd a, pdd b, pdd c) {
    // 叉乘
    return ((c.first - a.first) * (b.second - a.second) - (c.second - a.second) * (b.first - a.first)) < 0;
}

void jarvis_march(const vpdd &input) {

    int n = input.size();
    int left = 0;
    for (int i = 0; i < n; i++) {
        if (input[i].first < input[left].first) {
            left = i;
        }
    }

    int first_point = left;
    int third_point;
    do {
        hull_jmarch.push_back(input[first_point]);
        third_point = (first_point + 1) % n;
        for (int i = 0; i < n; i++) {
            if (ccw(input[first_point], input[i], input[third_point])) {
                third_point = i;
            }
        } 
        first_point = third_point;

    } while (first_point != left);
}

参考

• https://blog.csdn.net/viafcccy/article/details/87483567
• https://blog.csdn.net/u012328159/article/details/50808360
• https://blog.csdn.net/shungry/article/details/104340363