DCN and RepPoints
可变形卷积网络(DCN)和 RepPoints 的介绍,结合网络计算整理总结。
1 DCN (Deformable Convolution Network)
在计算机视觉领域,同一物体在不同场景、角度中未知的几何变换是检测/识别的一大挑战,通常来说有两种做法:
-
通过充足的数据增强,扩充足够多的样本去增强模型适应尺度变换的能力。
-
设置一些针对几何变换不变的特征或者算法,如 SIFT 和 sliding windows。
两种方法都有缺陷,第一种方法因为样本的局限性使得模型的泛化能力比较低;第二种方法则因为手工设计的不变特征和算法对于过于复杂的变换是很难的而无法设计。所以提出了Deformable Conv(可变形卷积)和 Deformable Pooling(可变形池化)来解决这个问题。
图-1 展示了卷积核大小为 的普通卷积和可变形卷积的采样方式。(a) 表示按照正常的卷积规律采样 9 个点(绿点),(b)©(d) 为可变形卷积,再正常的采样坐标上加了一个位移量(蓝色箭头),其中 ©(d) 为 (b) 的特殊情况,展示了可变形卷积可以作为尺度变换、比例变换和旋转变换的特殊情况。
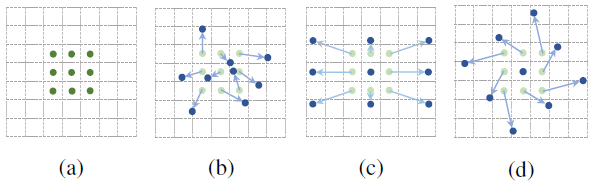
1.1 可变形卷积
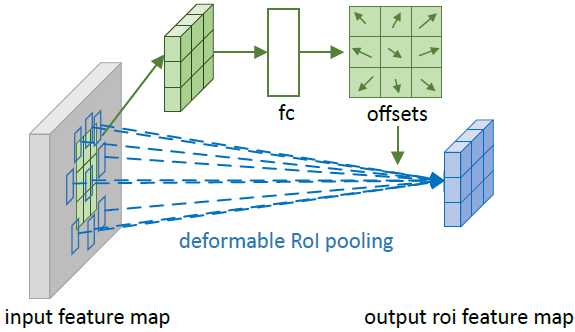
1.2 可变形卷积的可视化
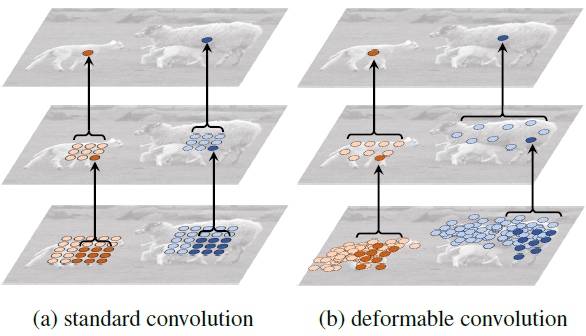

可以从图-4 看到,当绿色点在目标上时,红色点所在区域也集中在目标位置,并且基本能够覆盖不同尺寸的目标,因此经过可变形卷积,可以更好地提取出感兴趣物体的完整特征。
1.3 可变形池化
原始的 RoI Pooling 在操作过程中是将 RoI 划分为 个子区域(bin),最终得到 的 feature map,对于第 个 bin,有:
为 bin 中像素点的个数,对于第 个 bin,有:
新的 RoI Pooling 可以计算规则为:
可变形池化的偏移量其实就是子区域的偏移。每一个子区域都有一个偏移,偏移量对应子区域有 个。与可变形卷积不同的是,可变形池化的偏移量是通过全连接层得到的。对于可变形池化的偏移量,计算式子如下:
首先 RoI Pooling 产生 pooled feature map(图-2 中绿色部分),然后用 FC(Fully Connected)去学习归一化后的偏移值(归一化的目的是使偏移量学习不受 RoI 大小的影响),这个偏移量会与 做点乘,然后再乘以尺度因子 ,其中 是 RoI 的宽和高, 为 0.1。用该位移作用在可变形 RoI Pooling 上(蓝色区域),以获得不局限于 RoI 固定网格的特征。

调整后的 RoI bin 如红色框所示,此时并不是规则的将黄色框 RoI 等分为 的 bins。
1.4 Deformable Network
网络设置方面:
- 学习 offset 的参数采用的是0初始化,然后按照网络其它参数学习率的 倍来学习, 默认是 1,但在某些情况下,比如 Faster R-CNN 中的 fc 是 0.01。
- 并不是所有的卷积都换成可变形卷积就是好的,在提取到一些语义特征后使用可变形卷积效果会更好,一般来说是网络靠后的几层。
2 DCN v2
图-6 为普通卷积核 DCN v1 再三张图片上的展示结果,每一列代表检测不同的物体,从左向右,物体面积增大;每一行代表不同的表现形式,第一行为物体周围的感受野分布,第二行为有效的采样位置,第三行为得到能相同的响应的最小区域。从第三行可以很明显的看出,DCN v1 会增加无关信息。为了提高网络适应几何变化的能力,减少无关因素的影响,DCN v2 提出了改进以提高其建模能力并帮助它利用这种增强的功能。

DCN v2 提出了三种解决方法:
- More Deformable Conv Layers(使用更多的可变形卷积)。
- Modulated Deformable Modules(在 DCN v1 基础(添加 offset)上添加每个采样点的权重)
- R-CNN Feature Mimicking(模拟 R-CNN 的 feature)。
2.1 More Deformable Conv Layers
DCN v1 只在 ResNet-50 的 conv5 中使用了三个可变形卷积,而 DCN v2 在 conv3、conv4 和 conv5 的 卷积层中都使用了可变形卷积,得到如图-7 中的结果。
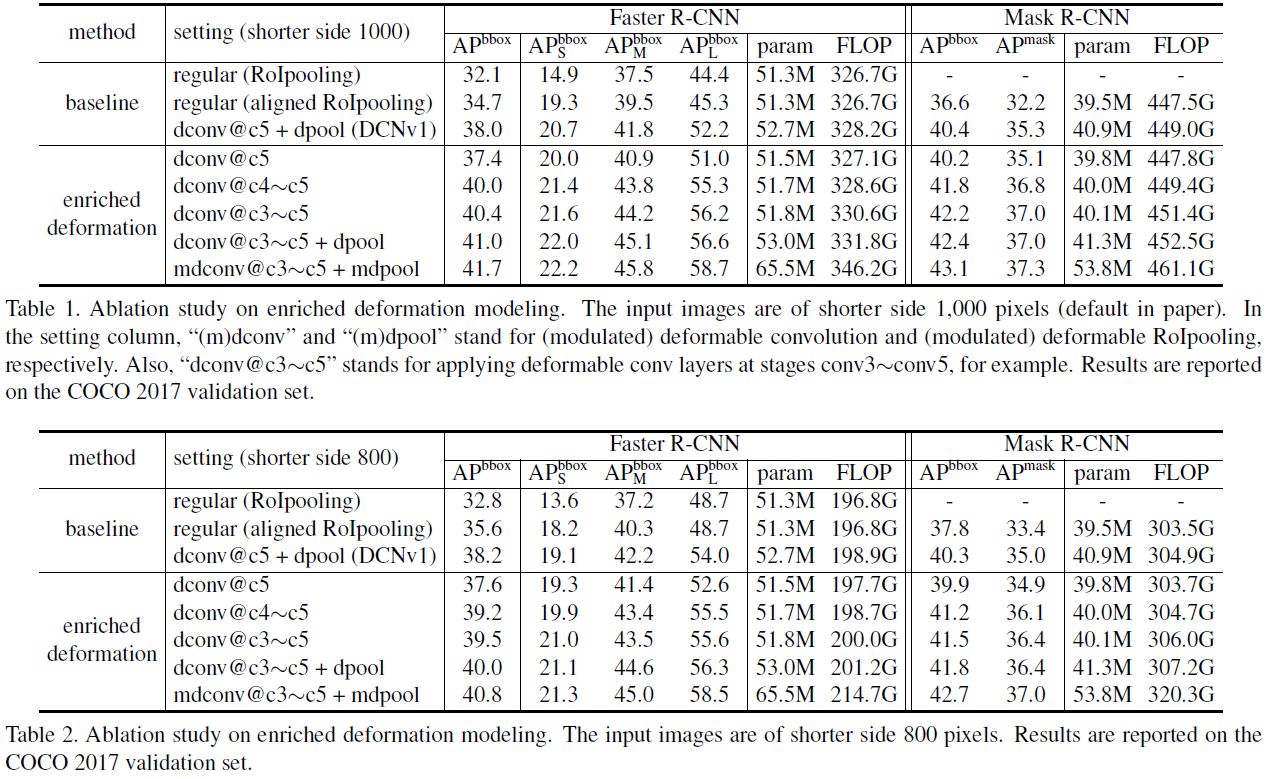
2.2 Modulated Deformable Modules
在 DCN v1 中,卷积只是添加了 offset 参数 :
或记 为卷积核的采样点个数, 为第 个采样点的卷积核权重和偏移,则上式可以写为:
为解决引入了一些无关区域的问题,DCN v2 中不只添加每一个采样点的偏移,还添加了一个权重系数 ,用于区分所引入的区域是否为感兴趣的区域。加入权重系数后,上式变为:
和 是学习到的 offset 和权重,这样的好处是增加了更大的自由度,对于不需要的采样点则设置权重为 0 即可(权重学习为 0)。
和 都是通过在相同的输入 feature map 上应用单独的卷积层获取,该卷积层具有与当前卷积层相同的空间分辨率,输出为 通道,其中前 对应于学习的偏移,剩余 进一步进入 Sigmoid 层用于获得权重,此卷积的卷积核初始为 0, 和 的初始值为 0 和 0.5,学习率为其他现有卷积层的 0.1 倍。
Modulated Deformable RoI Pooling 的式子也因权重的加入相应变为:
和 由输入特征图上的分支产生。在这个分支中,RoI Pooling 在 RoI 上生成特征,然后输入两个 1024-D 的 FC 层。然后在这些后面有一个额外的 FC 层,产生 的通道输出,前 是可学习的归一化偏移 ,后 是经 Sigmoid 标准化后产生的 ,额外的 FC 层的学习率和其他层相同。
2.3 R-CNN Feature Mimicking
把 R-CNN 和 Faster R-CNN 的 classification score 结合起来可以提升 performance,说明 R-CNN 学到的 focus 在物体上的 feature 可以解决 redundant context 的问题。但是增加额外的 R-CNN 会使 inference 速度变慢很多。DCN v2 里的解决方法是把 R-CNN 当做 teacher network,让 DCN v2 的 RoI Pooling 之后的 feature 去模拟 R-CNN 的 feature。
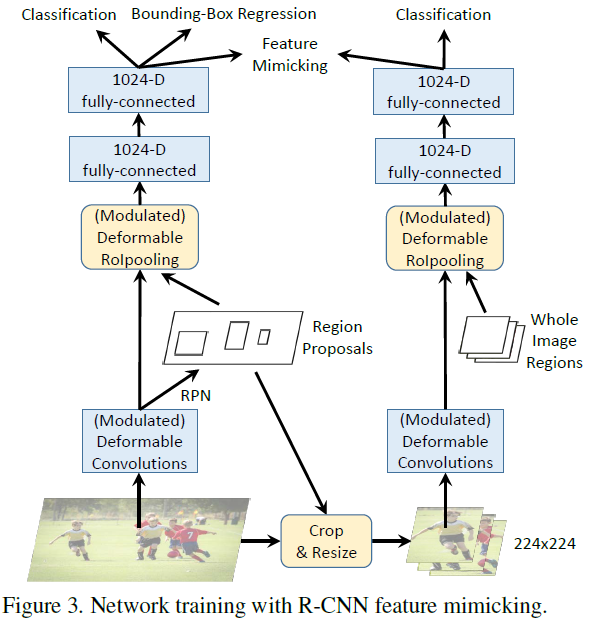
左边的网络为主网络(Faster R-CNN),右边的网络为子网络(R-CNN)。实现上大致是用主网络训练过程中得到的 RoI 去裁剪原图,然后将裁剪到的图 resize 到 大小作为子网络的输入,将裁剪的 RoI 区域记为 。在 R-CNN 分支中,骨干网络在调整大小的图像块上操作并产生 的特征图。可变形 RoI Pooling 层应用于特征图,其中输入 RoI 覆盖整个调整大小的图像块(左上角为 ,高度和宽度为 224 像素)。之后,应用 2 个 1024-D 层,产生输入图像的 R-CNN feature vector,表示为 。用 Softmax 分类器进行分类,其中 表示前景类别的数量,加上一个用于背景。在 R-CNN 特征表示 和 Faster R-CNN 中的对应物 之间执行 feature mimic loss,其也是 和 的余弦相似度,计算方法如下:
因为 R-CNN 这个子网络的输入就是 RoI 在原输入图像上裁剪出来的图像,因此不存在 RoI 以外区域信息的干扰,这就使得 R-CNN 这个网络训练得到的分类结果更加可靠,以此通过一个损失函数监督主网络 Faster R-CNN 的分类支路训练就能够使网络提取到更多 RoI 内部特征,而不是自己引入的外部特征。
总的 loss 由三部分组成:mimic loss + R-CNN classification loss + Faster-RCNN loss
在训练时,主干网络、Deformable RoIPooling和 2 个 FC 共享参数。inference 阶段,只用 Faster R-CNN 来测试。
3 RepPoints
在典型 anchor-based 的算法中,模型的效果往往受限于 anchor 的配置参数,如 anchor 大小、正负样本采样、anchor 的宽高比等。anchor-free 的算法无需配置 anchor 参数,即可训练得到一个好的检测模型,减少了训练前对数据复杂的分析过程。
anchor-free 算法又可分为基于 anchor-point 的算法和基于 key-point 的算法:
- anchor-point 算法本质上和 anchor-based 算法相似,通过预测目标中心点 及边框距中心点的距离 来检测目标,典型的此类算法有 FSAF、FCOS 等。
- key-point 方法是通过检测目标的边界点(如:角点),再将边界点配对组合成目标的检测框,此类算法包括 CornerNet、RepPoints 等。
经典的 bounding box 虽然有利于计算,但没有考虑目标的形状和姿态,而且从矩形区域得到的特征可能会受背景内容或其它的目标的严重影响,低质量的特征会进一步影响目标检测的性能。为了解决 bounding box 存在的问题,RepPoints 的提出能够进行更细粒度的定位能力以及更好的分类效果。
RepPoints 提出使用点集的方式来表示目标,该方法在不使用 anchor 的基础上取得了非常好的效果。如图-9 ,(a) 表示一般目标检测算法使用水平包围框来表示目标位置信息,(b) 则表示 RepPoints 使用点集来表示目标位置的方法。RepPoints 系列工作其实就是以点集表示为核心,从不同的角度去进一步提升该算法精度而做出改进:
- 将验证(即分割)的过程融入 RepPoints,进一步提升结果,得到 RepPoints V2;
- 将点集的监督方式进行改进,并扩充点集的点数,实现了目标实力分割任务的统一范式,即 Dense RepPoints。

3.1 RepPoints
bounding box 只是粗粒度的目标位置表示方法,只考虑了目标的矩形空间,没有考虑形状、姿态以及语义丰富的局部区域,而语义丰富的局部区域能够帮助网络更好的定位以及特征提取。为了解决上述的缺点,RepPoints 使用一组自适应的采样点表示目标:
表示目标的采样点数,RepPoints 原始论文中设为 9。
3.1.1 RepPoints Refinement
逐步调整 bounding box 定位和特征提取是 multi-stage 检测器成功的重要手段,对于 RepPoints,调整可简单地表示为:
为预测的新采样点相对与旧采样点的偏移值,采样点调整的尺寸都是一样的,不会像 bouning box 那样需要解决中心点坐标和边框长度的尺寸不一致问题。
3.1.2 Converting RepPoints to Bounding Box
为了利用 bounding box 的标注信息进行训练以及验证 RepPoint-based 检测算法的性能,使用预设的转化方法 将 RepPoints 转化成伪预测框( 表示物体 的 RepPoints, 表示相应的 pseudo box),共有三种转化方法:
- : Min-max function,对所有的 RepPoints 进行 min-max 操作来获取预测框
- :Partial min-max function,对部分的 RepPoints 进行 min-max 操作获取预测框
- :Moment-based function,通过 RepPoints 的均值和标准差计算中心点位置以及预测框尺寸得到预测框 ,尺寸通过全局共享的可学习参数 和 相乘得到
这些函数都是可微的,可加入检测器中进行 end-to-end 的训练。通过实验验证,这 3 个转化方法效果都不错。

3.2 RPDet: an Anchor Free Detector
anchor-free 的目标检测算法 RPDet 是基于 RepPoints 设计,包含两个识别阶段。因为可变形卷积可采样多个不规则分布的点进行卷积输出,所以可变形卷积十分适合 RepPoints 场景,能够根据识别结果的反馈进行采样点的引导。图-11 为 RPDet 的主要框架:
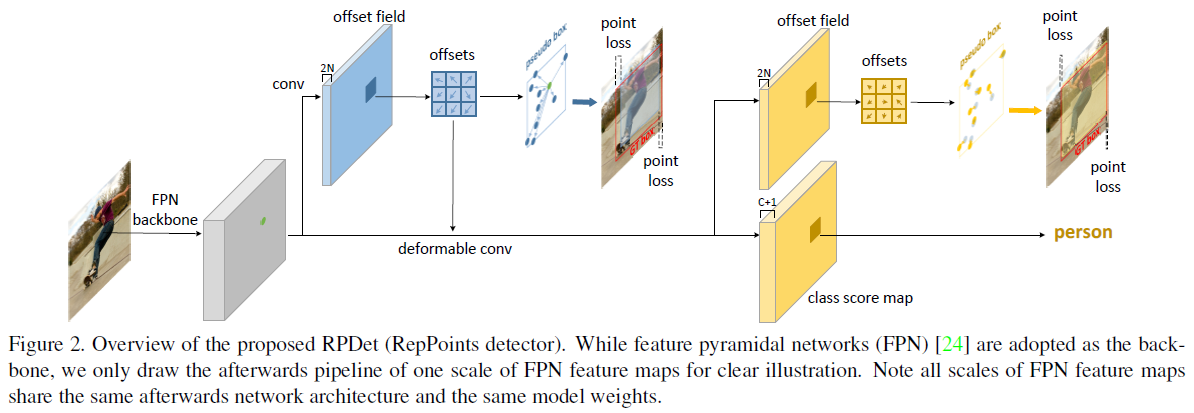
3.2.1 Center Point Based Initial Object Representation
RPDet 将中心点作为初始的目标表示,然后逐步调整出最终的 RepPoints,中心点也可认为是特殊的 RepPoints。当两个目标存在于特征图同一位置时,这种基于中心点的方法通常会出现识别目标歧义的问题。此前的方法在同一位置设置多个预设的 anchor 来解决此问题,而 RPDet 则利用 FPN 来解决此问题:
- 不同大小的目标由不同 level 的特征负责识别
- 小物体对应 level 的特征图一般较大,减少了同一物体存在同一位置的可能性
3.2.2 Utilization of RepPoints
如图-11 所示,RepPoints 是 RPDet 的基础目标表示方法,从中心点开始,第一组 RepPoints 通过回归中心点的偏移值获得。第二组 RepPoints 代表最终的目标位置,由第一组 RepPoints 优化调整得到。RepPoints 的学习主要由两个目标驱动:
- 伪预测框和 GT 框的左上角点和右上角点的距离损失
- 后续的目标分类损失
第一组 RepPoints 由距离损失和分类损失引导,第二组 RepPoints 仅使用距离损失进行引导,主要为了学习到更精准的目标定位。
3.2.3 Backbone and Head Architectures
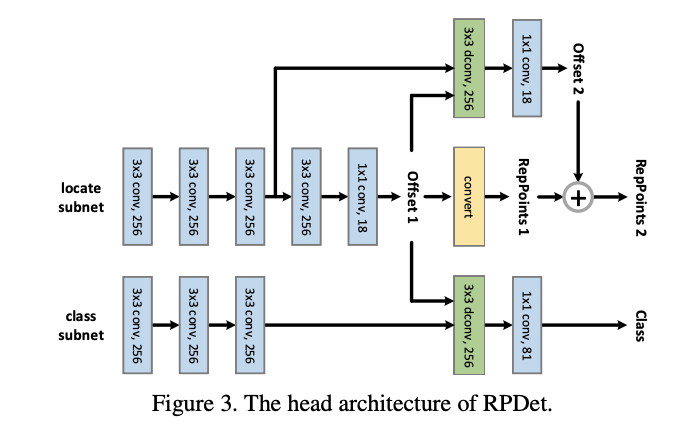
FPN 主干网络包含5层特征金字塔 level,从 stage3(下采样 8 倍)到 stage7(下采样 128 倍)。Head 的结构如图-12,Head 在不同的 level 中是共享的,包含两个独立的子网,分别负责定位(RepPoints 的生成)和分类:
- 定位子网首先使用 3 个 256-d 卷积提取特征,每个卷积都接 group normalization 层,然后连续接两个小网络计算两组 RepPoints 的偏移值。
- 分类子网首先使用 3 个 256-d 卷积提取特征,每个卷积都接 group normalization 层,然后将定位子网输出的第一组 RepPoints 的偏移值输入到 256-d 可变形卷积中进一步提取特征,最后输出分类结果。
尽管 RPDet 采用了两阶段定位,但其性能甚至比单阶段的 RetinaNet 要高,主要是 anchor-free 的设计使得分类层的计算减少了,覆盖了额外的定位阶段带来的少量消耗。
3.2.4 Localization/Class Target Assignment
如图-12,定位包含两个阶段,第一阶段从中心点得到第一组 RepPoints,第二阶段则从第一组 RepPoints 调整得到第二组 RepPoints,不同的阶段的正样本定义不同:
- 对于第一阶段,特征点被认为是正样本需满足:1) 该特征点所在的特征金字塔 level 等于 。2) 目标的中心点在特征图上映射位置对应该特征点。
- 对于第二阶段,只有特征点对应的第一阶段产生的伪预测框与目标的 IoU 大于 0.5 才被认为是正样本。与当前的 anchor-based 方法有点类似,将第一阶段的输出当作 anchor。
由于目标的分类只考虑第一组 RepPoints,所以,特征点对应的第一组 RepPoints 产生的伪预测框于目标的 IoU 大于 0.5 即认为是正样本,小于 0.4 则认为是背景类,其它则忽略。
附 空洞卷积(Dilated Convolution)
Appendix.1 空洞卷积
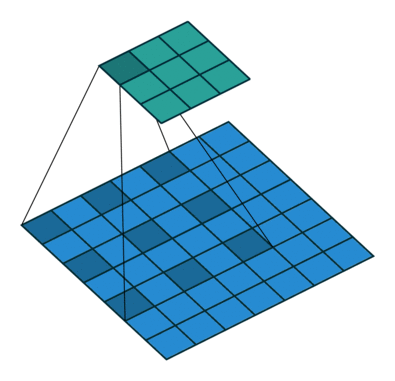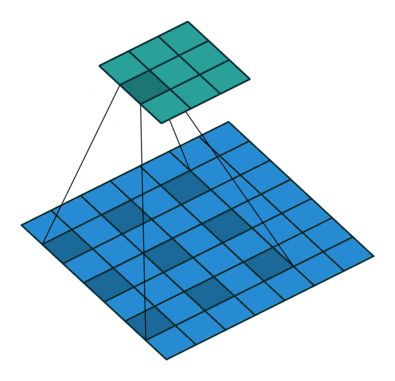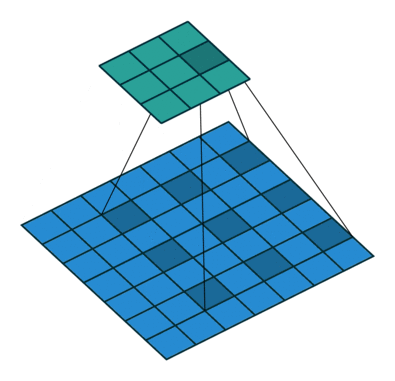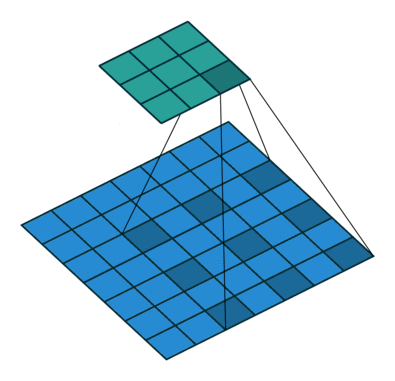
如图.附-1 所示就是空洞卷积,这里 。空洞卷积有两种理解:
- 理解为将卷积核扩展,如图卷积核为 但是这里将卷积核变为 ,即在卷积核每行每列中间加0 。
- 理解为在特征图上每隔 1 行或 1 列取数与 卷积核进行卷积。
改变 stride 和 padding,空洞卷积就会和图.附-1 有区别。
Appendix.2 空洞卷积的感受野
CNN 的感受野为:
为本层感受野, 为上层感受野, 是第 层卷积或池化的步长, 为卷积核的大小,例(初始感受野为 1):
- 第一层 卷积():,感受野为
- 第二层 池化():,感受野为
- 第三层 卷积():,感受野为
- 第四层 卷积():,感受野为
空洞卷积的感受野计算方法和上面相同,空洞可以理解为扩大了卷积核的大小,空洞卷积的感受野变化(卷积核大小为 ,):
- 第一层 1-dilated conv: 的空洞卷积为普通的 卷积,因此 ,感受野为
- 第二层 2-dilated conv: 的空洞卷积可以理解为卷积核变为了 ,因此 ,感受野为
- 第三层 4-dilated conv: 的空洞卷积可以理解为卷积核变味了 ,因此 ,感受野为
可以看到将卷积以上面的过程叠加,感受野变化会指数增长,感受野公式为
上文所述该计算公式是基于叠加的顺序,如果单用三个 的 2-dilated 卷积则感受野使用卷积感受野计算公式计算:
- 第一层 的 2-dilated 卷积:
- 第二层 的 2-dilated 卷积:
- 第三层 的 2-dilated 卷积:
参考
References.1 RepPoints
- https://zhuanlan.zhihu.com/p/64522910
- https://zhuanlan.zhihu.com/p/260656201
- https://segmentfault.com/a/1190000040265117
- https://blog.csdn.net/weixin_43711554/article/details/104983391
References.2 DCN
- https://blog.csdn.net/qq_41917697/article/details/116193042
- https://zhuanlan.zhihu.com/p/180075757
- https://zhuanlan.zhihu.com/p/339660219
- https://zhuanlan.zhihu.com/p/52578771