Epipolar Geometry

Posted on Edited on In Waline:

对极几何（Epipolar Geometry）是 Structure from Motion 问题中，在两个相机位置产生的两幅图像之间存在的一种特殊几何关系，是 SfM 问题中 2D-2D 求解两帧间相机姿态的基本模型。

本文结合网络资源对对极几何进行整理。

Epipolar Gemotry

1 基本概念

对极几何（Epipolar Geometry）是 Structure from Motion 问题中，在两个相机位置产生的两幅图像之间存在的一种特殊几何关系，是 SfM 问题中 2D-2D 求解两帧间相机姿态的基本模型。

2 基本模型

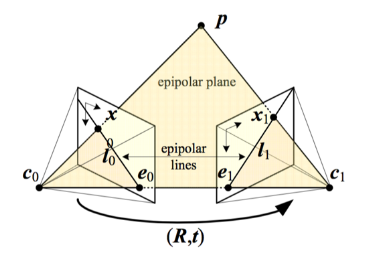
图中 c0,c1c_0, c_1 为两个相机中心，p\bold{p} 为空间中一点，p\bold{p} 在 c0,c1c_0, c_1 对应的像平面上的投影分别为 x0,x1\bold{x}_0, \bold{x}_1。c0,c1c_0, c_1 连线与像平面的交点 e0,e1e_0, e_1 为极点（epipole），l0,l1\bold{l}_0, \bold{l}_1 为极线（epipolar line），c0,c1,pc_0, c_1, p 三点组成的平面称为极平面（epipolar plane）。

3 对极约束

根据针孔相机模型，相机成像平面一点的像素坐标 p\bold{p} 和该点在世界坐标系下的 3D 坐标 P\bold{P} 有 p=KP\bold{p} = \bold{KP} 的关系，使用齐次坐标则有：

dp=KP(3.1)d \bold{p} = \bold{KP} \tag{3.1}

其中 dd 为点深度，K\bold{K} 为内参矩阵，p\bold{p} 为齐次坐标。

以第一个相机的坐标系为参照，对于两个相机则有：

d0p0=K0P, d1p1=K1(RP+t)(3.2)d_0 \bold{p}_0 = \bold{K}_0 \bold{P},\ d_1 \bold{p}_1 = \bold{K}_1 (\bold{RP} + \bold{t}) \tag{3.2}

令 x=K−1p\bold{x} = \bold{K}^{-1} \bold{p}，则上式可以归一化为：

d0x0=P, d1x1=RP+t(3.3)d_0 \bold{x}_0 = \bold{P},\ d_1 \bold{x}_1 = \bold{RP} + \bold{t} \tag{3.3}

由这两式得：

d1x1=R(d0x0)+t⇒t×d1x1=t×Rd0x0+t×t (叉乘 t)⇒t×d1x1=t×Rd0x0⇒x1T(t×d1x1)=x1T(t×Rd0x0)⇒d1x1Tt∧x1=d0x1Tt∧Rx0(3.4)\begin{aligned} &d_1 \bold{x}_1 = \bold{R} (d_0 \bold{x}_0) + \bold{t} \\ \Rightarrow &\bold{t} \times d_1 \bold{x}_1 = \bold{t} \times \bold{R} d_0 \bold{x}_0 + \bold{t} \times \bold{t}\ (\text{叉乘}\ \bold{t}) \\ \Rightarrow &\bold{t} \times d_1 \bold{x}_1 = \bold{t} \times \bold{R} d_0 \bold{x}_0 \\ \Rightarrow &\bold{x}^T_1 (\bold{t} \times d_1 \bold{x}_1) = \bold{x}^T_1 (\bold{t} \times \bold{R} d_0 \bold{x}_0) \\ \Rightarrow &d_1 \bold{x}_1^T \bold{t}^{\wedge} \bold{x}_1 = d_0 \bold{x}_1^T \bold{t}^{\wedge} \bold{R} \bold{x}_0 \end{aligned} \tag{3.4}

由于等号左边左乘 x1T\bold{x}_1^T 为乘了一个与自身（t∧x1\bold{t}^{\wedge} \bold{x}_1）垂直的向量，因此等于 0，故而：

x1Tt×Rx0=x1Tt∧Rx0=0(3.5)\bold{x}^T_1 \bold{t} \times \bold{R} \bold{x}_0 = \bold{x}^T_1 \bold{t}^{\wedge} \bold{R} \bold{x}_0 = 0 \tag{3.5}

上式即为对极约束。

对极约束的几何意义：

  • x1,t,Rx0\bold{x}_1, \bold{t}, \bold{R} \bold{x}_0 三者的混合积为 0，即三个向量共勉，即上图中三角形的三边共面。

4 本质矩阵

令 E=t×R=t∧R\bold{E} = \bold{t} \times \bold{R} = \bold{t}^{\wedge} \bold{R}，得到对极约束的新形式：

x1TEx0=0(4.1)\bold{x}_1^T \bold{E} \bold{x}_0 = 0 \tag{4.1}

E\bold{E} 称为本质矩阵（Essential Matrix），由外参 R\bold{R} 和 t\bold{t} 决定。

本质矩阵的几何意义：

  • x1Tl1=0\bold{x}_1^T \bold{l}_1 = 0，即 x1\bold{x}_1 在直线 l1=Ex0\bold{l}_1 = \bold{E} \bold{x}_0 上，表示 E\bold{E} 将 x0\bold{x}_0 投影到另一幅图像中的直线 l1\bold{l}_1 上。

5 基本矩阵

引入相机内参矩阵，将像点映射到像素平面：

{p0=K0x0p1=K1x1(5.1)\begin{cases} \bold{p}_0 = \bold{K}_0 \bold{x}_0 \\ \bold{p}_1 = \bold{K}_1 \bold{x}_1 \end{cases} \tag{5.1}

带入本质矩阵的 (4.1) 式可得：

p1TK1−TEK0−1p0=0(5.2)\bold{p}_1^T \bold{K}_1^{-T} \bold{E} \bold{K}_0^{-1} \bold{p}_0 = 0 \tag{5.2}

令 F=K1−TEK0−1\bold{F} = \bold{K}_1^{-T} \bold{E} \bold{K}_0^{-1}，上式变为：

p1TFp0=0(5.3)\bold{p}_1^T \bold{F} \bold{p}_0 = 0 \tag{5.3}

F\bold{F} 称为基本矩阵（Fundamental Matrix），表示了同一 3D 点在两个相机像素平面上像素点之间的几何约束关系。

本征矩阵与基本矩阵表征了两个透视模型对极几何的代数特征，以上 (4.1) 和 (5.2) 二式共同构成对极约束（Epipolar Constraint）。

参考