本文结合网络资源对匈牙利算法进行整理。
匈牙利算法
1 指派问题
假设有三位工人 A,B,C,需要分配每人完成一件工作;对于不同的工作他们索要不同的工钱,如下表所示。问题就是要找到一套开销最小的指派方案。
| . |
工作1 |
工作2 |
工作3 |
| A |
1 |
3 |
3 |
| B |
3 |
1 |
3 |
| C |
3 |
3 |
1 |
使用匈牙利方法可以找到开销最小的方案,即 A 负工作 1,B 负责工作 2,C 负责工作 3,总开销为 3。
2 匈牙利算法的矩阵形式
给定 n 位工人以及 n 件工作,可以用一个 n×n 的开销矩阵来表示这一指派问题:
\left[
\begin{matrix}
a_1 & a_2 & a_3 & a_4\\
b_1 & b_2 & b_3 & b_4\\
c_1 & c_2 & c_3 & c_4\\
d_1 & d_2 & d_3 & d_4
\end{matrix}
\right]
$$ {]}
其中 $a, b, c, d$ 表示工人,下标 $1, 2, 3, 4$ 表示工作,$x_y$ 表示指派工人 $x$ 负责工作 $y$ 的开销。
# 3 匈牙利算法步骤
- 算法核心思想:一件大的事物若除去一件小的事物,对这件事没有多大影响。
## Step 1 对开销矩阵的各行进行操作
- 找出每一行中值最小的元素,然后把该行所有元素都减去这一最小值
完成后矩阵的每一行至少会出现一个 $0$。假如 $a_1, b_4, c_2, d_3$ 是开销矩阵每行的最小值,则开销矩阵在完成本项操作后变成:
\left[
\begin{matrix}
0 & a_2-a_1 & a_3-a_1 & a_4-a_1\
b_1-b_4 & b_2-b_4 & b_3-b_4 & 0\
c_1-c_2 & 0 & c_3-c_2 & c_4-c_2\
d_1-d_3 & d_2-d_3 & 0 & d_4-d_3
\end{matrix}
\right]
这个矩阵每行都有一个 $0$,而且这些 $0$ 分布于**不同的列**,那么开销最小的指派方案就出来了,就是
a\rightarrow1, b\rightarrow4, c\rightarrow2, d\rightarrow3
执行完这一步后,开销矩阵中的 $0$ 元素很可能没有**分布于不同的行列**:
\left[
\begin{matrix}
a_1 & 0 & a_3 & a_4\
0 & b_2 & b_3 & b_4\
c_1 & c_2 & c_3 & 0\
0 & d_2 & d_3 & d_4
\end{matrix}
\right]
那么继续进行下一步计算。
## Step 2 对开销矩阵的各**列**进行操作
- 找出每一列中值最小的元素,然后把该列所有元素都减去这一最小值
这一步之后,如果 $0$ 分布于不同的行列,则得到了最优解;如果以每个 $0$ 为中心画十字、被十字覆盖的其余 $0$ 不再画十字,所有的 $0$ 都画十字后仍有元素未被覆盖,则说明指派未完成,继续进行下一步。
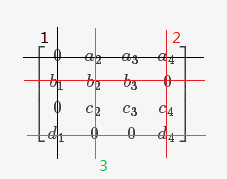
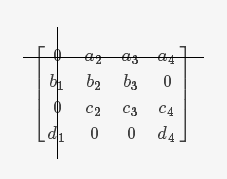
## Step 3 用尽量少的横线或竖线覆盖矩阵中的所有 $0$
\left[
\begin{matrix}
0 & a_2 & a_3 & a_4\
b_1 & b_2 & b_3 & 0\
0 & c_2 & c_3 & c_4\
d_1 & 0 & 0 & d_4
\end{matrix}
\right]
假设对上矩阵做计算寻找最优分配:
### 3.1 尽可能多的分配
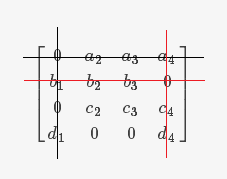
(1)第一行有一个 $0$,所以把 $1$ 分配给 $a$。由于 $1$ 已经分配出去,所以位于第三行第一列的 $0$ 不再被考虑。
(2)第二行有一个 $0$,所以把 $4$ 分配给 $b$。
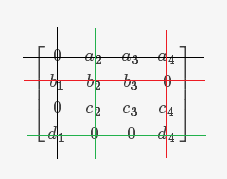
(3)第三行原本有一个 $0$,但由于 $1$ 已经被分配出去,所以不予以考虑,不能给 $c$ 分配。
(4)第四行有两个未被覆盖的 $0$,但只能给 $d$ 一项,另一项未被分配的任务要划掉、本轮不予以考虑。
### 3.2 用最少的线覆盖所有 $0$
(1)标记所有上一步后仍未得到任务的工人
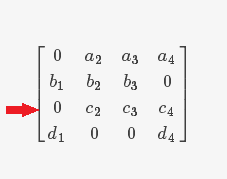
(2)标记所有**刚被标记过的行中** $0$ 所在的列
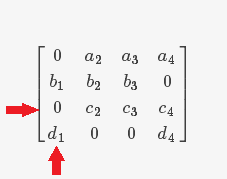
(3)标记所有刚被标记过的列中 $0$ 所在的行
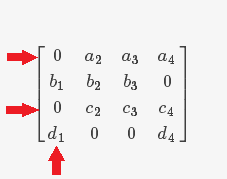
(4)对仍未得到任务的工人(矩阵的行)重复以上 3 步
(5)在所有标记过的列和未标记的行上画线
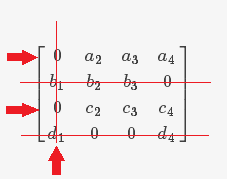
- 经过以上画线操作,所有的 $0$ 就被最少的线覆盖
## Step 4
- 从上一步中未被覆盖的元素中找到最小值,然后把这些元素都减去最这一小值、给直线交叉点的元素加上这一最小值
## Step 5
- 重复 Step-3 和 Step-4,直到所有任务都被分配
# 参考
- https://blog.csdn.net/u011837761/article/details/52058703
- https://zhuanlan.zhihu.com/p/96229700