Occupancy Grid Map

Posted on Edited on In Waline:

对论文 OA-SLAM: Leveraging Objects for Camera Relocalization in Visual SLAM (ISMAR, 2022) 的阅读整理。

占位栅格图

1 Occupancy Map 简介

将空间划分为一个个小网格（cell），每个 cell 中存储 cell 内是否有障碍物的概率，这样的地图称为 Occupancy Map，由于所有 cell 构成一个网，所以也称为 Grid Map。

以 2D Occupancy Map 为例，每个 cell 中都有一个概率，那整个地图可以看做一个描述障碍物分布的概率分布（须将所有 cell 中的概率值归一化）。构建地图的过程，就是根据传感器（比如 LiDAR）的观测，更新这个概率分布。

设每个 cell 的概率相对于其他 cell 是独立的，更新地图的概率分布就简化为更新每个 cell 的概率。即在已知 11 到 tt 时刻所有观测的情况下，该 cell 中有障碍物的概率，记为：

p(mi∣y1:t)p (m^i | y_{1:t})

2 占位栅格图（Occupancy Grid Map）

图-1 图像栅格化

如上图，将车辆行驶的道路环境用网格（cell）切分，并且每个 cell 用二值数值 0 和 1 填充，0 表示该 cell 被占用，1 表示该网格 cell 没有被占用，即此处

mi∈{0,1}m^i \in \{0, 1 \}

由此得到如下的栅格占位图：

图-2 占位栅格地图

制作理想的占位栅格地图必须满足以下几个假设条件：

  1. 占位栅格地图是对道路行驶区域中的静态环境（static environment）的描述。意味着，在制图前必须将地面、动态物体（车辆、行人等）从传感器数据中移除；

  2. 每个网格 cell 与其它的所有网格的状态是相互独立的，即它的状态不受周围其它网格状态的影响；

  3. 在每个时刻，车辆的位置是精确的、已知的。

3 概率占位栅格图（Probabilistic Occupancy Grid Map）

实际应用中，车辆传感器的数据测量存在误差，车辆的定位结果也存在误差，动态障碍物的识别也存在误差，因此用概率表示一个 cell 被占用的可能性是更加可行的方案。每个网格存储一个 [0,1][0, 1] 之间的概率值，值越大，表示网格被占用的可能性越大，如下图所示。

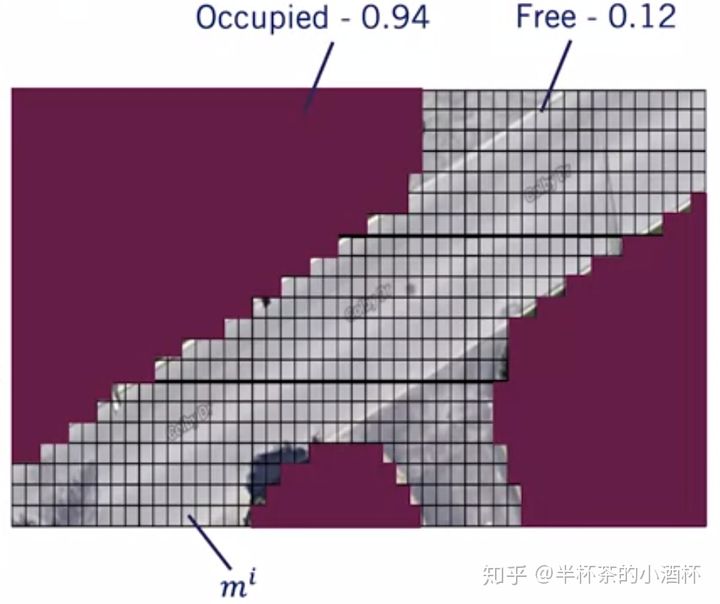
图-3 概率占位栅格地图

4 概率占位栅格图的制图

栅格图每个 cell 的概率值计算公式为：

belt(mi)=p(mi∣y1:t)bel_t (m^i) = p (m^i | y_{1:t})

其中 y1:ty_{1:t} 是 11 到 tt 时刻车辆位置和传感器测量结果，通过历史信息的累计提升制作的地图的准确性。可以通过贝叶斯理论将历史信息融合：

belt(mi)=ηp(yt∣mi)belt−1(mi)bel_t (m^i) = \eta p(y_t | m^i) bel_{t-1}(m^i)

其中 η\eta 是归一化参数，p(yt∣mi)p(y_t | m^i) 是传感器的测量模型。

4.1 贝叶斯理论更新存在的问题

由上面的贝叶斯迭代更新式子，因为概率值为小于 1 的浮点数，那么长期重复的浮点数运算将会导致计算结果的数值越来越小而难以精确表达和运算。因此，可以使用 Logit 函数把变量从 (0,1)(0,1) 单调映射至 (−∞,∞)(-\infty, \infty)：

Logit⁡(x)=f(x)=log⁡x1−x\operatorname{Logit}(x) = f(x) = \log \frac{x}{1-x}

因此，可以使用 Logit 函数替代标准的贝叶斯更新过程。

4.2 贝叶斯更新过程

贝叶斯理论更新 cell 占用概率的公式如下：

p(mi∣y1:t)=p(yt∣y1:t−1,mi)p(mi∣y1:t−1)p(yt∣y1:t−1)(1)p(m^i | y_{1:t}) = \frac{p(y_t | y_{1:t-1}, m^i) p(m^i | y_{1:t-1})}{p(y_t | y_{1:t-1})} \tag{1}

根据一阶马尔科夫假设，tt 时刻的状态只与 t−1t-1 时刻的状态有关，因此上式可以写为：

p(mi∣y1:t)=p(yt∣mi)p(mi∣y1:t−1)p(yt∣y1:t−1)(2)p(m^i | y_{1:t}) = \frac{p(y_t | m^i) p(m^i | y_{1:t-1})}{p(y_t | y_{1:t-1})} \tag{2}

对测量模型使用贝叶斯更新过程：

p(yt∣mi)=p(mi∣yt)p(yt)p(mi)(3)p(y_t | m^i) = \frac{p(m^i | y_t) p(y_t)}{p(m^i)} \tag{3}

将公式 (3) 带入 (2) 得到：

p(mi∣y1:t)=p(mi∣yt)p(yt)p(mi∣y1:t−1)p(mi)p(yt∣y1:t−1)(4)p(m^i | y_{1:t}) = \frac{p(m^i | y_t) p(y_t) p(m^i | y_{1:t-1})}{p(m^i) p(y_t | y_{1:t-1})} \tag{4}

计算 1−p1-p：

p(¬mi∣y1:t)=1−p(mi∣y1:t)=p(¬mi∣yt)p(yt)p(mi∣y1:t−1)p(¬mi)p(yt∣y1:t−1)(5)p(\lnot m^i | y_{1:t}) = 1 - p(m^i | y_{1:t}) = \frac{p(\lnot m^i | y_t) p(y_t) p(m^i | y_{1:t-1})}{p(\lnot m^i) p(y_t | y_{1:t-1})} \tag{5}

因此有：

p1−p=p(mi∣y1:t)p(¬mi∣y1:t)=p(mi∣yt)p(yt)p(mi∣y1:t−1)p(mi)p(yt∣y1:t−1)p(¬mi∣yt)p(yt)p(mi∣y1:t−1)p(¬mi)p(yt∣y1:t−1)=p(mi∣yt)p(¬mi)p(mi∣y1:t−1)p(¬mi∣yt)p(mi)p(¬mi∣y1:t−1)=p(mi∣yt)(1−p(mi))p(mi∣y1:t−1)(1−p(mi∣yt))p(mi)(1−p(mi∣y1:t−1))(6)\begin{aligned} \frac{p}{1-p} &= \frac{p(m^i | y_{1:t})}{p(\lnot m^i | y_{1:t})} = \frac{\frac{p(m^i | y_t) p(y_t) p(m^i | y_{1:t-1})}{p(m^i) p(y_t | y_{1:t-1})}}{\frac{p(\lnot m^i | y_t) p(y_t) p(m^i | y_{1:t-1})}{p(\lnot m^i) p(y_t | y_{1:t-1})}} \\ &= \frac{p(m^i | y_t) p(\lnot m^i) p(m^i | y_{1:t-1})}{p(\lnot m^i | y_t) p(m^i) p(\lnot m^i | y_{1:t-1})} \\ &= \frac{p(m^i | y_t) (1 - p(m^i)) p(m^i | y_{1:t-1})}{(1 - p(m^i | y_t)) p(m^i) (1 - p(m^i | y_{1:t-1}))} \end{aligned} \tag{6}

带入 Logit 函数，即对 (6) 两侧取对数，整理得到：

logit⁡(p(mi∣y1:t))=logit⁡(p(mi∣yt))+logit⁡(p(mi∣y1:t−1))−logit⁡(p(mi))(7)\operatorname{logit}(p(m^i | y_{1:t})) = \operatorname{logit}(p(m^i | y_t)) + \operatorname{logit}(p(m^i | y_{1:t-1})) - \operatorname{logit}(p(m^i)) \tag{7}

因此，得到贝叶斯更新递推公式：

lt,i=logit⁡(p(mi∣yt))+lt−1,i−l0,il_{t, i} = \operatorname{logit}(p(m^i | y_t)) + l_{t-1, i} - l_{0, i}

其中，logit⁡(p(mi∣yt))\operatorname{logit}(p(m^i | y_t)) 是 Inverse Measurement Model，lt−1,il_{t-1, i} 是网格 ii 在 t−1t-1 时刻的置信度（belif），l0,il_{0,i} 是 initial belif。由此，关键则是如何计算 Inverse Measurement Model。

4.3 Inverse Measurement Model

以 2D LiDAR 扫描模型来说明（此处 2D LiDAR 是为了简化模型，而实际使用则把理论推广到 3D LiDAR）。

4.3.1 2D LiDAR

在 2D 平面上扫描，使用两个参数 scanner bearings 和 scanner rangers：

  • scanner bearings 均匀分布在 [−ϕmaxs,ϕmaxs][-\phi_{max}^s, \phi_{max}^s]，一般可以认为均匀分布在 360° 的各个方向上；
  • scanner rangers 是从 LiDAR 中心到障碍物的距离，范围为 [0,rmaxs][0, r_{max}^s]，此处假设 LiDAR 发射激光后立即收到回波，不存在时间延迟。

4.3.2 Map 坐标系、Vehicle 坐标系和传感器坐标系

假设在 2D LiDAR 在 Map 坐标系中的姿态为 (x1,t,x2,t,x3,t)(x_{1,t},x_{2,t},x_{3,t})，前面两个值表示 x 和 y 坐标，后面一个表示传感器朝向。通过姿态，可以将 2D LiDAR 测量结果转换到 Map 坐标系。

4.3.3 LiDAR 测量结果雨 Map cell 相关联

如下图所示，第 ii 个 Map cell 用 (ri,ϕi)(r_i, \phi_i) 表示：

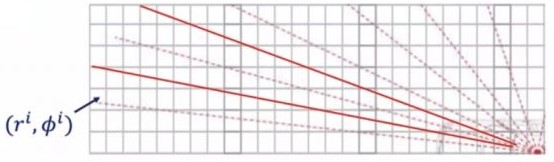
图-4 Map cell 的表示

Relative range: ri=(mxi−x1,t)2+(myi−x2,t)2Relative bearing: ϕi=arctan⁡myi−x2,tmxi−x1,t−x3,t\mathrm{Relative\ range:\ } r_i = \sqrt{(m^i_x - x_{1,t})^2 + (m^i_y - x_{2,t})^2} \\ \mathrm{Relative\ bearing:\ } \phi_i = \arctan \frac{m^i_y - x_{2,t}}{m^i_x - x_{1,t}} - x_{3,t}

通过 2D LiDAR bearing 与 Map cell 相对于传感器的方位进行最小误差匹配，得到影响当前 Map cell 的激光束：

k=argmin⁡∣(ϕi−ϕis)∣k = \operatorname{argmin} |(\phi_i - \phi_i^s)|

匹配过程，先定义 α\alpha 和 β\beta，各个 cell 的概率计算如下：

  1. 如果 ri>rmaxsr_i > r_{max}^s 或 ∣ϕi−ϕks∣>β/2|\phi_i - \phi_k^s| > \beta/2，表示为探测区域，没有信息，这些区域的概率值一般为 0.5，表示不确定是否被占用。
  2. 如果 rks<rmaxsr_k^s < r_{max}^s 且 ∣ri−rks<α/2∣|r_i - r_k^s < \alpha/2|，表示该区域大概率被占用，因此要赋予一个大于0.5的概率值。
  3. 如果 ∣ri−rks∣>α/2|r_i - r_k^s| > \alpha/2，这些网格被占用的概率较低，因此赋予一个小于 0.5 的概率值。

参考