RetinaNet

Posted on 2022-06-02 Edited on 2023-02-01 In Summary Waline:

本文是关于 RetinaNet 相关网络资料的整理。

RetinaNet

1 目标检测的 Two Stage 和 One Stage

1.1 Two Stage 和 One Stage

Two Stage：第一级专注于 proposal 的提取，第二级对提取出的 proposal 进行分类和精确坐标回归。两级结构准确度较高，但因为第二级需要单独对每个 proposal 进行分类/回归，处理速度上就受到了影响。例如 Faster-RCNN。

One Stage：摒弃了提取 proposal 的过程，只用一级就完成了识别和回归，速度较快但准确率远不比两级结构。例如 SSD，YOLO。

1.2 类别失衡

类别失衡（Class Imbalance）是产生精度差异的主要原因：

One Stage 方法在得到特征图后，会产生密集的目标候选区域，而这些大量的候选区域中只有很少部分是真正的目标，这就造成了机器学习中经典的训练样本正负不平衡的问题。它往往会造成最终算出的 training loss 为占绝对多数但包含信息量却很少的负样本所支配，少样正样本提供的关键信息却不能在一般所用的 training loss 中发挥正常作用，从而无法得出一个能对模型训练提供正确指导的 loss。
Two Stage 方法得到 proposal 后，其候选区域要远远小于 One Stage 产生的候选区域，因此不会产生严重的类别失衡问题。
常用的解决此问题的方法就是负样本挖掘，或其它更复杂的用于过滤负样本从而使正负样本数维持一定比率的样本取样方法。RetinaNet 中提出了 Focal Loss 来对最终的 Loss 进行校正。

2 Focal Loss

Focal Loss 是在原有的交叉熵损失函数上增加了一个因子，让损失函数更加关注 hard examples。下面是用于二值分类的交叉熵损失函数，其中 $y\in \{\pm1\}$ 为真实类别标签， $p\in[0,1]$ 是模型预测的 $y=1$ 的概率：

$CE(p,y)= \begin{cases} -\log{(p)} &\mathrm{if}\ \ y=1 \\ -\log{(1-p)} &\mathrm{otherwise} \end{cases}$

定义：

$p_t= \begin{cases} p, &\mathrm{if}\ \ y=1 \\ 1-p, &\mathrm{otherwise} \end{cases}$

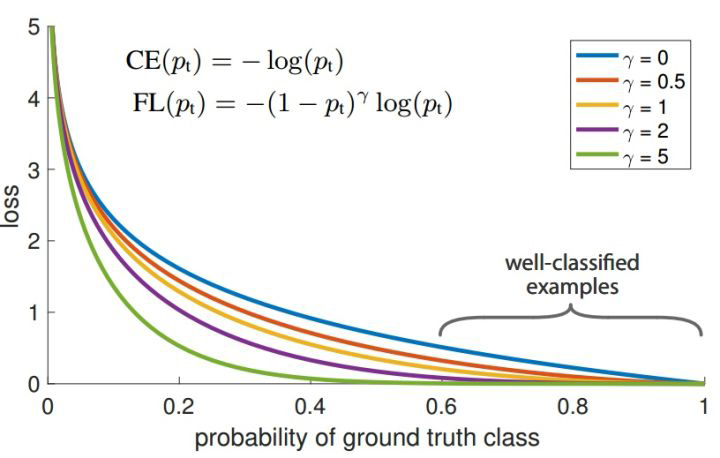
因此交叉熵可以写成如下形式，其曲线如图-1 中蓝色曲线：

$CE(p,y)=CE(p_t)=-\log{(p_t)}$

由图-1 中蓝色曲线，可以认为当预测模型得到的 $p_t\ge0.6$ 的样本为容易分类的样本，而 $p_t$ 值预测较小的样本为 hard examples，最后整个网络的 loss 就是所有训练样本经过模型预测得到的值的累加，因为 hard examples 通常为少数样本，所以虽然其对应的 loss 值较高，但是全部累加后，大部分的 loss 值来自于容易分类的样本，这样在模型优化的过程中就会将更多的优化放到容易分类的样本中，而忽略 hard examples。

对于这种类别不均衡问题常用的方法是引入一个权重因子 $\alpha$ ，对于类别 $+1$ 的使用权重 $\alpha$ ，对于类别 $-1$ 使用权重 $1-\alpha$ ：

$CE(p_t)=-\alpha_t\log{(p_t)}$

但采用这种加权方式可以平衡正负样本的重要性，但无法区分容易分类的样本与难分类的样本。因此，RetinaNet 中提出在交叉熵前增加一个调节因子 $(1-p_t)^\gamma$ ，其中 $\gamma$ 为 focusing parameter，且 $\gamma\ge0$ ，此时的公式为：

$FL(p_t)=-(1-p_t)^\gamma\log(p_t)$

$\gamma$ 取不同值时对应的曲线如图-1 所示。由图-1 可以发现，当 $\gamma$ 越来越大时，loss 函数在容易分类的部分其 loss 几乎为零，而 $p_t$ 较小的部分（hard examples 部分）loss 值仍然较大，这样就可以保证在类别不平衡较大时，累加样本 loss，可以让 hard examples 贡献更多的 loss，从而可以在训练时给与 hard examples 部分更多的优化。

在实际应用中，RetinaNet 还提出可以在 Focal Loss 的基础上，增加平衡因子 $\alpha_t$ ，从而产生轻微的精度提升：

$FL(p_t)=-\alpha_t(1-p_t)^\gamma\log(p_t)$

图-1 损失曲线

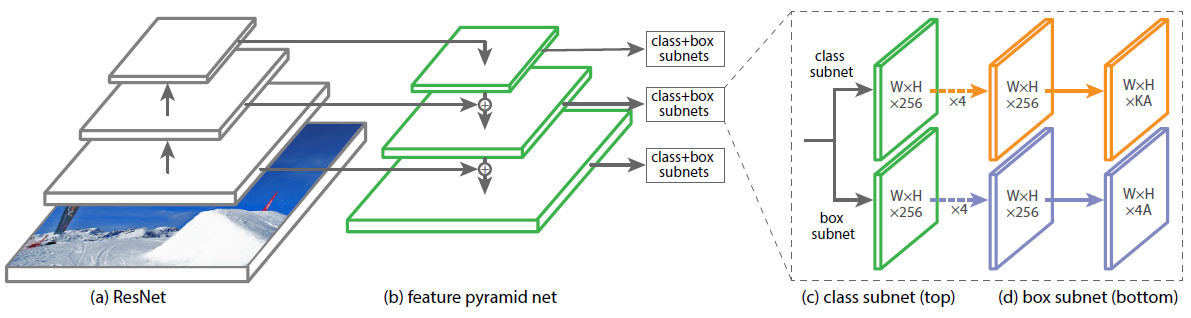
3 RetinaNet

图-2 是 RetinaNet 的网络结构，整个网络主要由 ResNet+FPN+2×FCN 子网络构成：

图-2 RetinaNet

3.1 Backbone

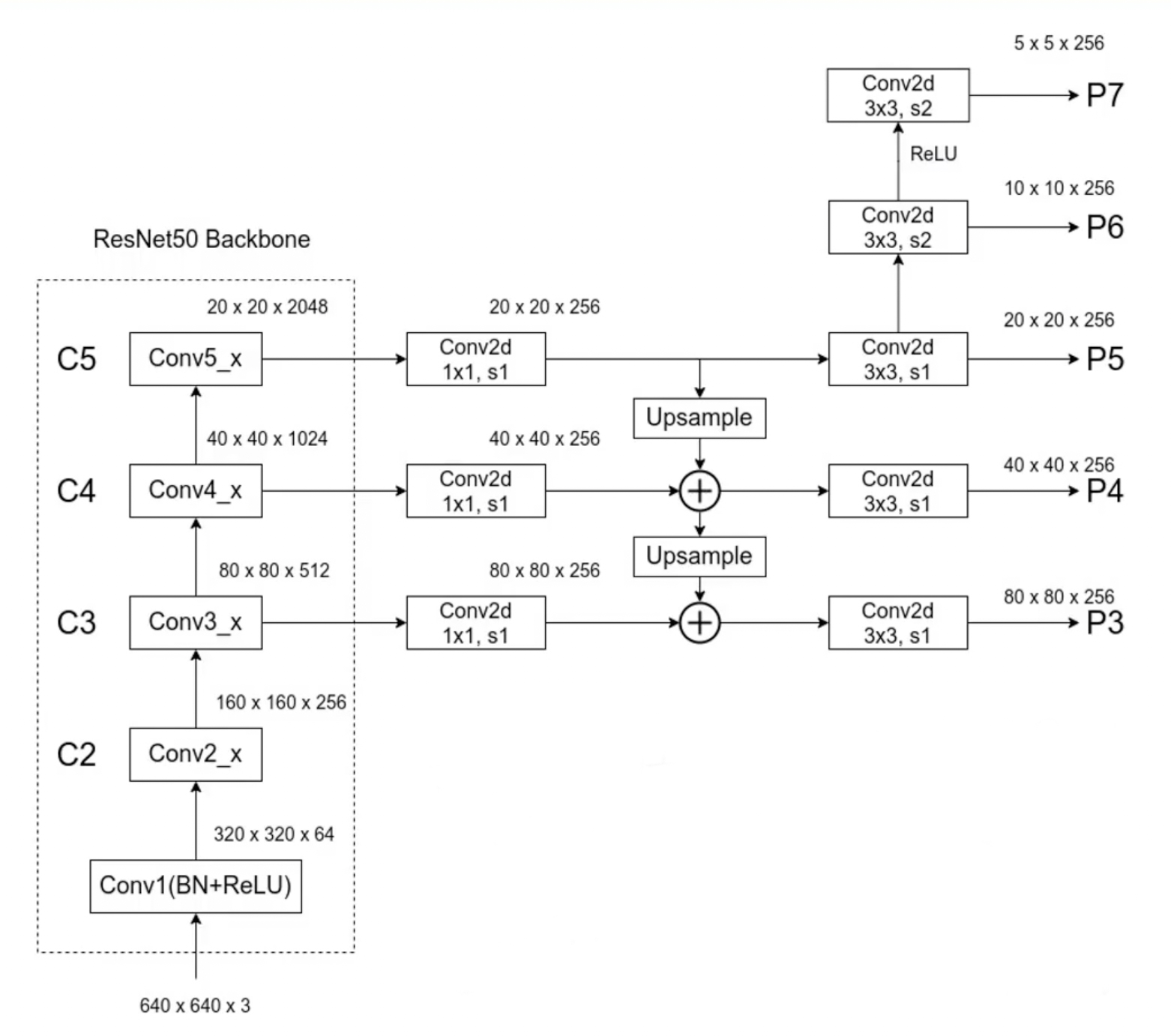
RetinaNet 的 backbone 部分如图-3 所示（图中 s2 表示 stride 为 2）：

图-3 RetinaNet的backbone部分（PyTorch官网提供的实现方法）

不同点：

与 FPN 不同，FPN 会使用到 C2，而 RetinaNet 因为考虑到 C2 生成的 P2 会占用更多的计算资源而没有使用。
对于 P6，RetinaNet 的原论文中是基于 C5 生成（最大池化下采样得到），而图-3 来自于 PyTorch 官方的实现，通过 $3\times3$ 卷积层下采样实现。
FPN 是从 P2 到 P6，而 RetinaNet 是从 P3 到 P7。

FPN 中每个特征层上使用了一个 scale（缩放比）和三个 ratio（纵横比），而 RetubaNet 是三个 scale 和三个 ratio 共计 9 个 anchor。RetinaNet 所使用的 scale 和 ratio 如下表。注意这里 scale 等于 $32$ 其对应的 anchor 的面积是 $32^2$ ，在 RetinaNet 中最小的 scale 是 $32$ ，最大的则是 $512\times2^{\frac{2}{3}}\approx813$ 。

Scale	Ratios
$32\{2^0,2^{\frac{1}{3}},2^{\frac{2}{3}}\}$	$\{1:2,1:1,2:1\}$
$64\{2^0,2^{\frac{1}{3}},2^{\frac{2}{3}}\}$	$\{1:2,1:1,2:1\}$
$128\{2^0,2^{\frac{1}{3}},2^{\frac{2}{3}}\}$	$\{1:2,1:1,2:1\}$
$256\{2^0,2^{\frac{1}{3}},2^{\frac{2}{3}}\}$	$\{1:2,1:1,2:1\}$
$512\{2^0,2^{\frac{1}{3}},2^{\frac{2}{3}}\}$	$\{1:2,1:1,2:1\}$

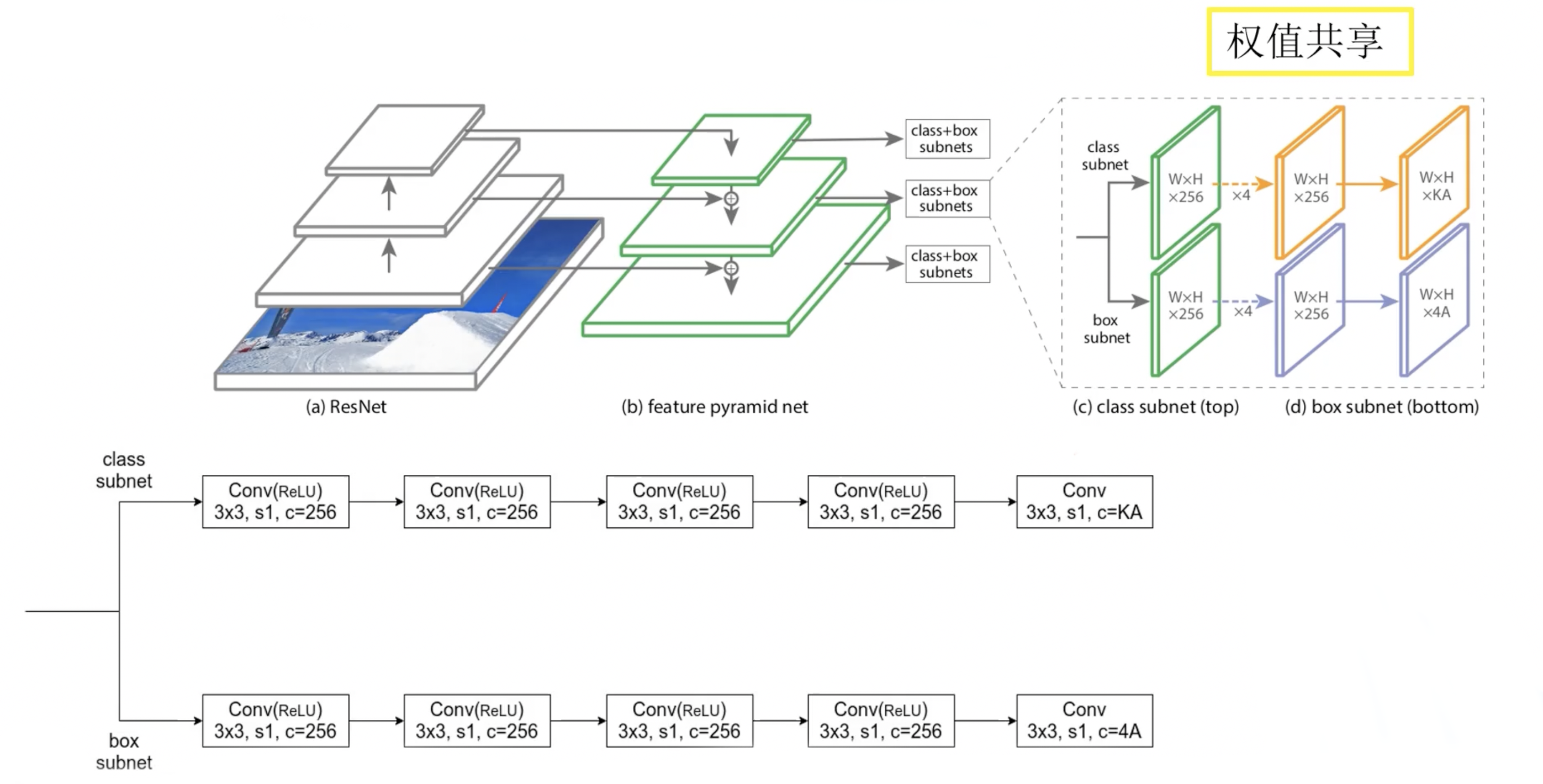
3.2 预测器

由于 RetinaNet 是 One Stage 的网络，所以不用 RoI Pooling，直接使用图-4 中权重共享的基于卷积操作的预测器。预测器分为两个分支，分别预测每个 anchor 所属的类别，以及目标边界框回归参数。最后的 $kA$ 中 $k$ 是检测目标的类别个数， $k$ 不包含背景类别； $A$ 是预测特征层在每一个位置生成的 anchor 的个数，此处为 9。

图-4 RetinaNet中预测器的结构

3.3 正负样本匹配

对每一个 anchor 与事先标注好的 GT box 进行比对，如果 IoU 大于 0.5 则是正样本，如果某个 anchor 与所有的 GT box 的 IoU 值都小于 0.4，则是负样本。其余的舍弃。

3.4 损失函数

总损失分为两部分，分类损失和回归损失：

$\begin{aligned} \mathcal{Loss} &=\frac{1}{N_{pos}}\sum_i \mathcal{L}_{cls}^i + \frac{1}{N_{pos}}\sum_j \mathcal{L}_{reg}^j \\ \mathcal{L}_{cls} &\text{: Sigmoid\ Focal\ Loss} \\ \mathcal{L}_{reg} &\text{: L1\ Loss} \\ N_{pos} &\text{: Number of Positive Samples} \\ i &\text{: All Positive/Negative Samples} \\ j &\text{: All Positive Samples} \end{aligned}$

参考

源码

https://link.zhihu.com/?target=https%3A//github.com/yhenon/pytorch-retinanet