Sparse Convolution
稀疏卷积常用于 3D 项目,如 3D 点云分割,由于点云数据是稀疏的,无法使用标准的卷积操作。同理,2D 任务中,如果只处理其中一部分像素,也需要使用稀疏卷积,这样有助于模型加速。本文是关于稀疏卷积的相关网络资料的整理。
1 介绍
稀疏卷积常用于 3D 项目,如 3D 点云分割,由于点云数据是稀疏的,无法使用标准的卷积操作。同理,2D 任务中,如果只处理其中一部分像素,也需要使用稀疏卷积,这样有助于模型加速。
原理:通过建立哈希表,保存特定位置的计算结果。
2 卷积的举例定义
2.1 输入数据
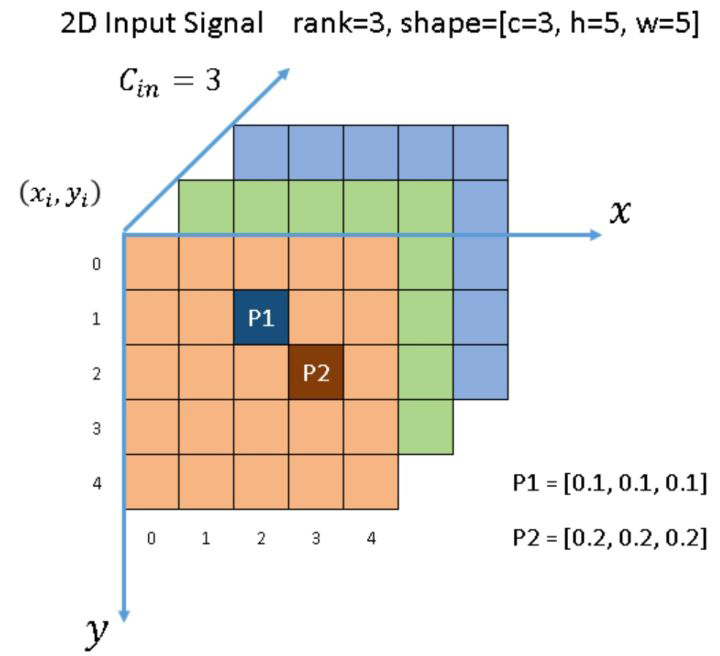
如图-1,有一个 3 channels 的 图像,除点 和 外,所有像素都是 ,而如 和 此类非零元素,也称为 activate input sites。输入张量按 顺序为 ,在稀疏形式下, 的数据列表为 ,索引列表为 ,注意索引的坐标顺序为 。
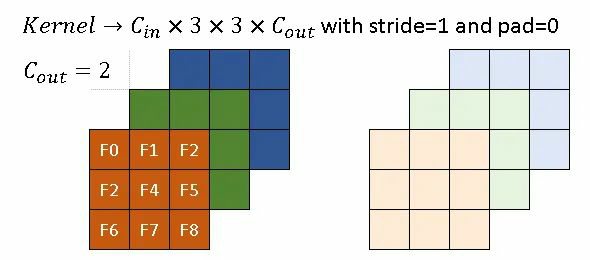
2.2 卷积核
稀疏卷积的卷积核和传统卷积相同,如图-2 所示,其核大小为 ,深色和浅色分别代表两个卷积核,即使得输出图像的 channel 数变为 。
2.3 输出数据
稀疏卷积的输出与传统卷积有很大不同,其输出有两种定义:
- regular output:和普通卷积一样,只要卷积核覆盖一个输入点(activate input site)就计算输出点;
- submanifold output:只有当卷积核中心覆盖输入点时,才计算输出。
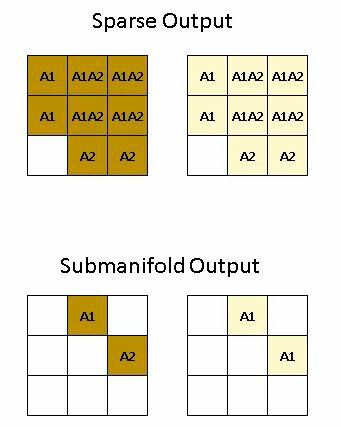
如图-3,输入图像为 ,卷积核为 ,stride 为 1,padding 为 0,输出张量的尺寸为 :
- sparse output 即为 regular output,例如 位置的 就表示输出只与 有关, 位置为 表示输出与 都有关。
- 第二种输出即为 submanifold output,只有当卷积核中心覆盖点 或 时才发生计算。
- 图-3 中两种颜色对应两个卷积通道。
3 计算实现
3.1 建立哈希表
建立输入、输出张量的序号-坐标哈希表,以 regular output definition 输出为例,如图-4。
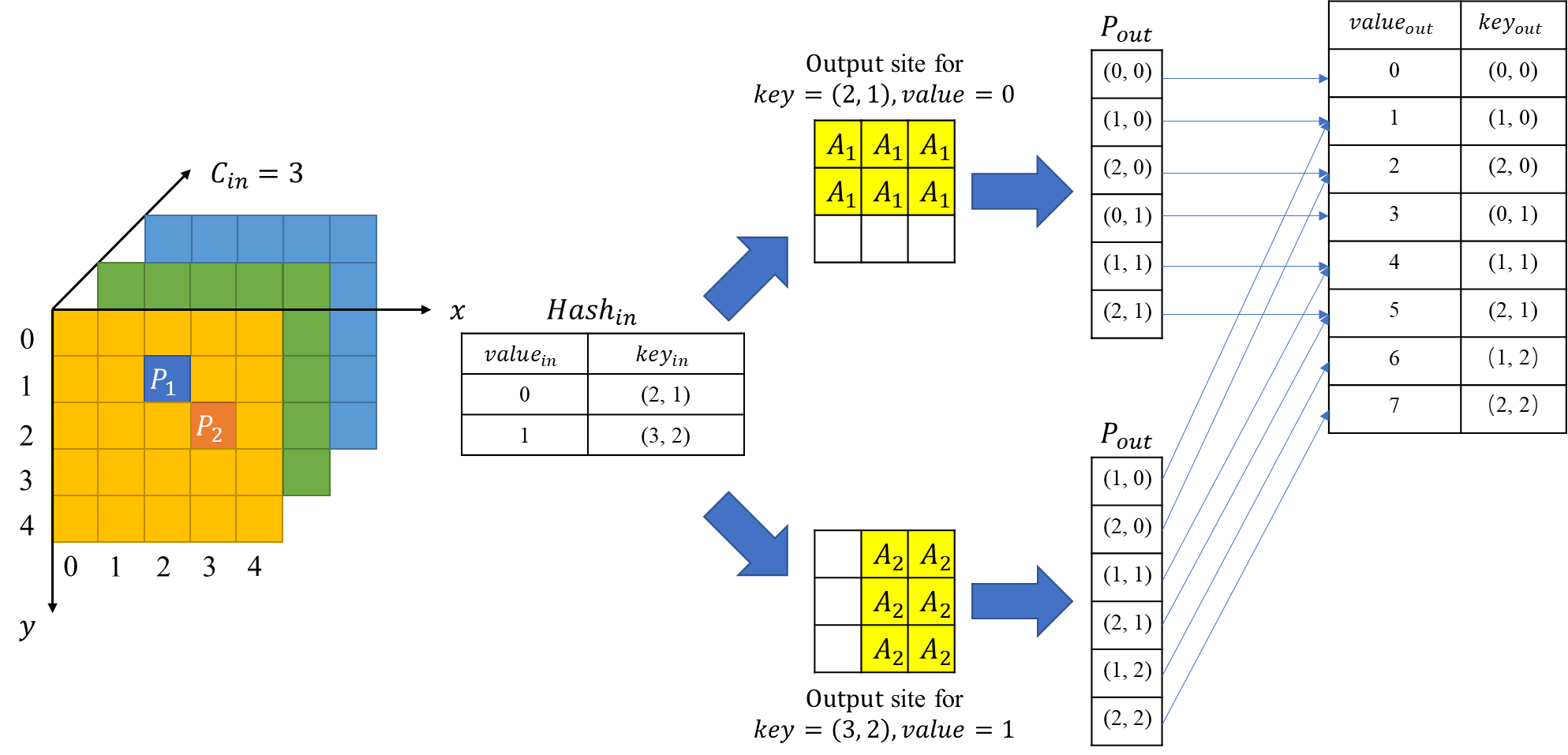
首先,建立输入哈希表 ,表中 表示输入像素的坐标, 表示序号(序号和坐标也可以颠倒),每一行表示一个 activate input site。那么,对于 输入来说,在 中则有 ,。
对于输出张量,与 相关的像素点有 6 个 位置,将这 6 个点的坐标记为 。通过 建立 , 表示输出张良的坐标, 表示序号,这样就建立了 的前 6 行。然后处理 ,输出张量中与 相关的(包含 )也有 6 个像素点,建立 的 ,会发现 与 有重复的部分,不管重复的部分,将非重复的部分写入 中,序号随之对应赋值。
3.2 建立 RuleBook
RuleBook 本质是一个表,哈希表将输入、输出张量坐标映射到序号,而 RuleBook 将输入、输出的哈希表中的序号建立起联系,以基本实现稀疏卷积,因此建立 RuleBook 是实现系数卷积的关键。如图-5 则是 RuleBook 的示例:
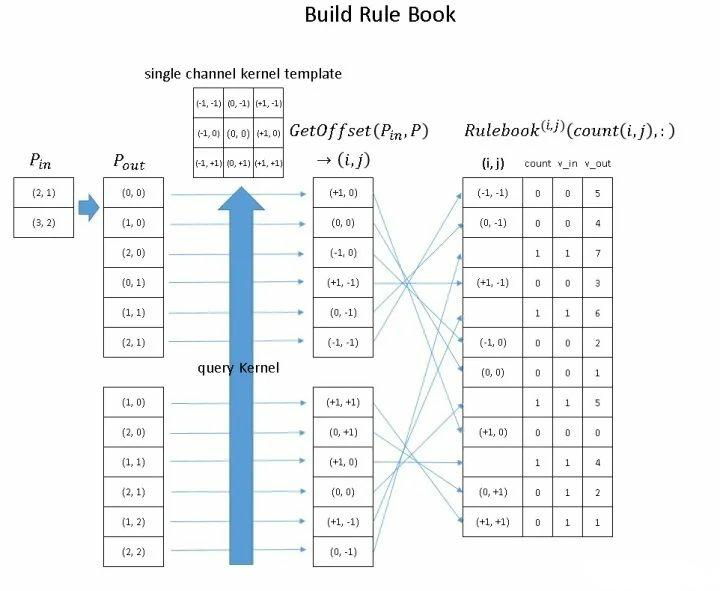
3.2.1 从 到
如图-6 所示, 的输入图像经过 的卷积核得到 的 output。以 output 中 位置为例,该点由 input 左上角的 窗口卷积得到,在这个窗口中只有 位置非零,其余均为零。那么,在这个窗口的卷积只需通过 对应的卷积权重及 点的值即可计算得到。 点对应的卷积权重位置为 ,将这个位置放入 中。
注意到, 点对应的卷积权重位置 实际上是这个权重位置在卷积核中相对于卷积核中心点的偏移。
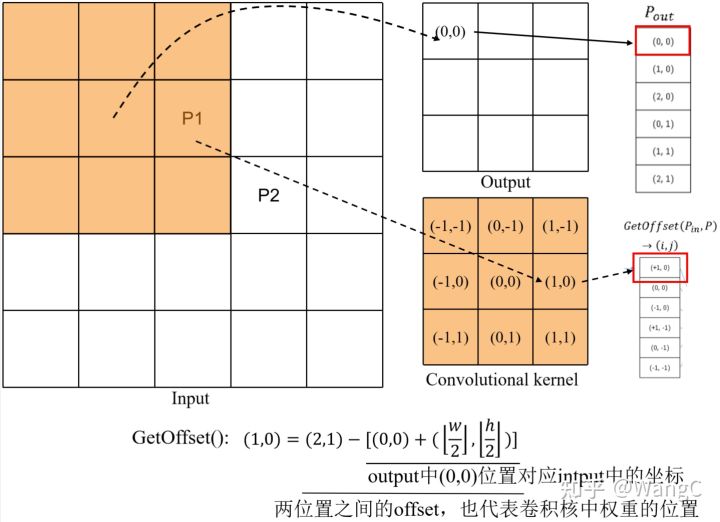
通过推导上述过程,可以得到 的计算公式,仍然以 点为例,公式为:
- 为 在 input 中的坐标;
- 为正处理的 output 某个值的坐标;
- 为 output 的大小;
- 为填入 的值。
公式中需要注意满足条件 。 的目的就是用于找出 output 中某位置需要用卷积核中的哪个权重来进行计算。
3.2.2 从 到
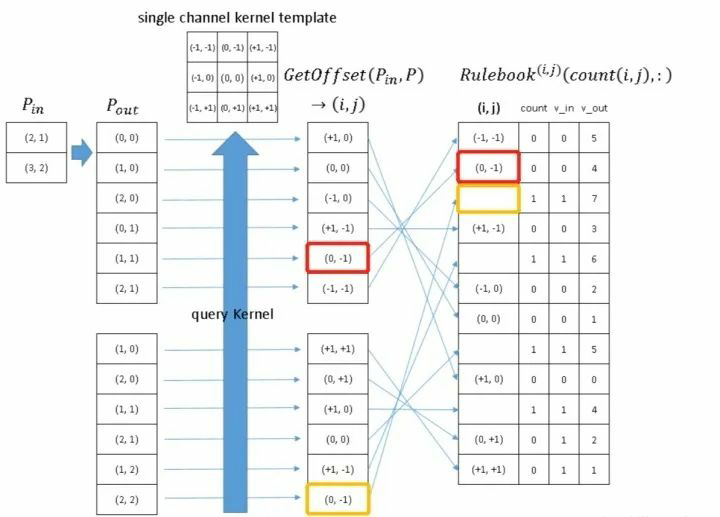
上一步完成了记录卷积核权重的位置,这一步则是记录对应的输入像素值以及计算完后存放的位置。如图-7,RuleBook 中红色框为前一步所记录的卷积核权重位置,橙色方框为输入像素值的输入序号 ,绿色方框为卷积结果对应的输出序号 。
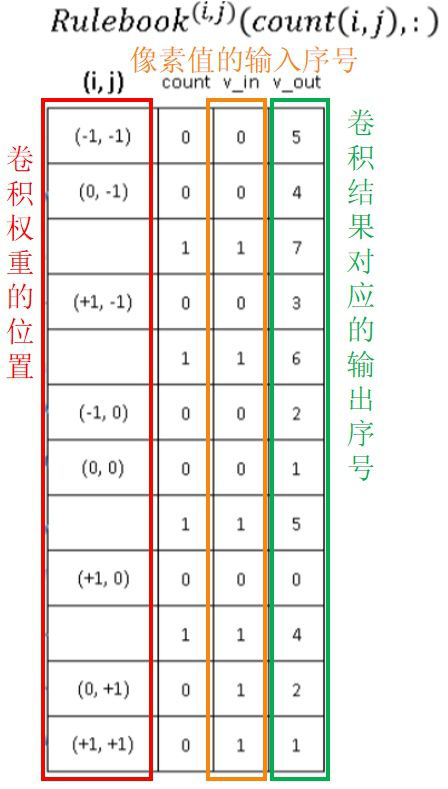
而对于 RuleBook 中的 列,其关系如图-8,会发现经由 和 得到的 中存在相同的卷积权重位置,例如 ,因此需要通过 列来进行计数,并利用对应行来表明此时重复位置对应的 和 。
3.2.3 计算过程
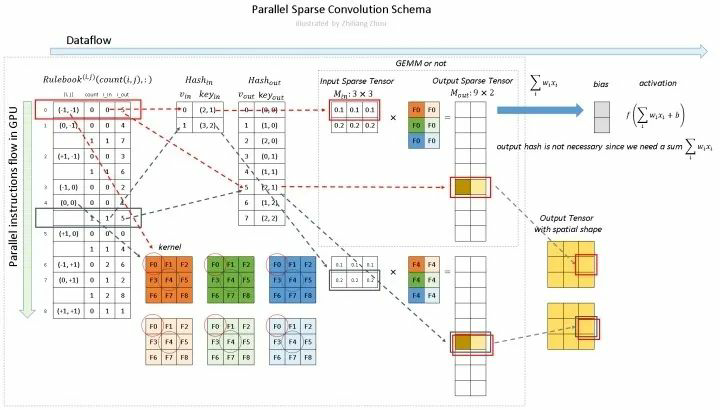
稀疏卷积的实现通过 RuleBook 来完成,可以通过 GPU 并行完成,因此计算效率较高。如图-9,以红色框中的计算为例,计算过程如下:
- 通过 找到卷积核权重 ;
- 根据输入像素序号 ,查找到对应的 ,从而可以查找到对应 的输入张量 ;
- 将 和深色和浅色两个卷积核进行计算,得到深黄色和浅黄色两个输出,同时由 值可以得到输出的填放位置 ;
- 需要注意,在图-9 的例子中,红色和蓝色两个方框的输出其 均为 5,即输出结果需要填放在同一位置 ,则将两个输出累加后再填入输出的 位置。
注意:上述计算过程跳过了 Output Sparse Tensor 部分,尺寸为 (output 的尺寸为 ,且 output 的通道数为 ),该部分为计算结果到最终 output 的一个中间张量,用于暂存计算结果,计算结束后,通过 即可将 Output Sparse Tensor 变化为最终的 output。