TSDF & Marching Cube

TSDF（基于截断的带符号距离函数）算法，是一种在 3D 重建中计算 iso-surface 的方法。在拥有大内存的显卡并行计算的情况下，可以做到实时重建的效果。

MC 是 W.Lorensen 等人于 1987 年提出来的一种体素级重建方法。MC 算法也被称为“等值面提取”（Iso-surface Extraction）算法。

本文是关于 TSDF 和 Marching Cube 相关网络资料的理论整理。

TSDF & Marching Cube

1 TSDF（Truncated Signed Distance Function）

1.1 简介

TSDF（基于截断的带符号距离函数）算法，是一种在 3D 重建中计算 iso-surface 的方法。在拥有大内存的显卡并行计算的情况下，可以做到实时重建的效果。

1.2 算法思路

用一个大空间（volume），这个空间可以完全包括要建立的 3D 模型，volume 由许多 voxel 构成：

图-1 Volume

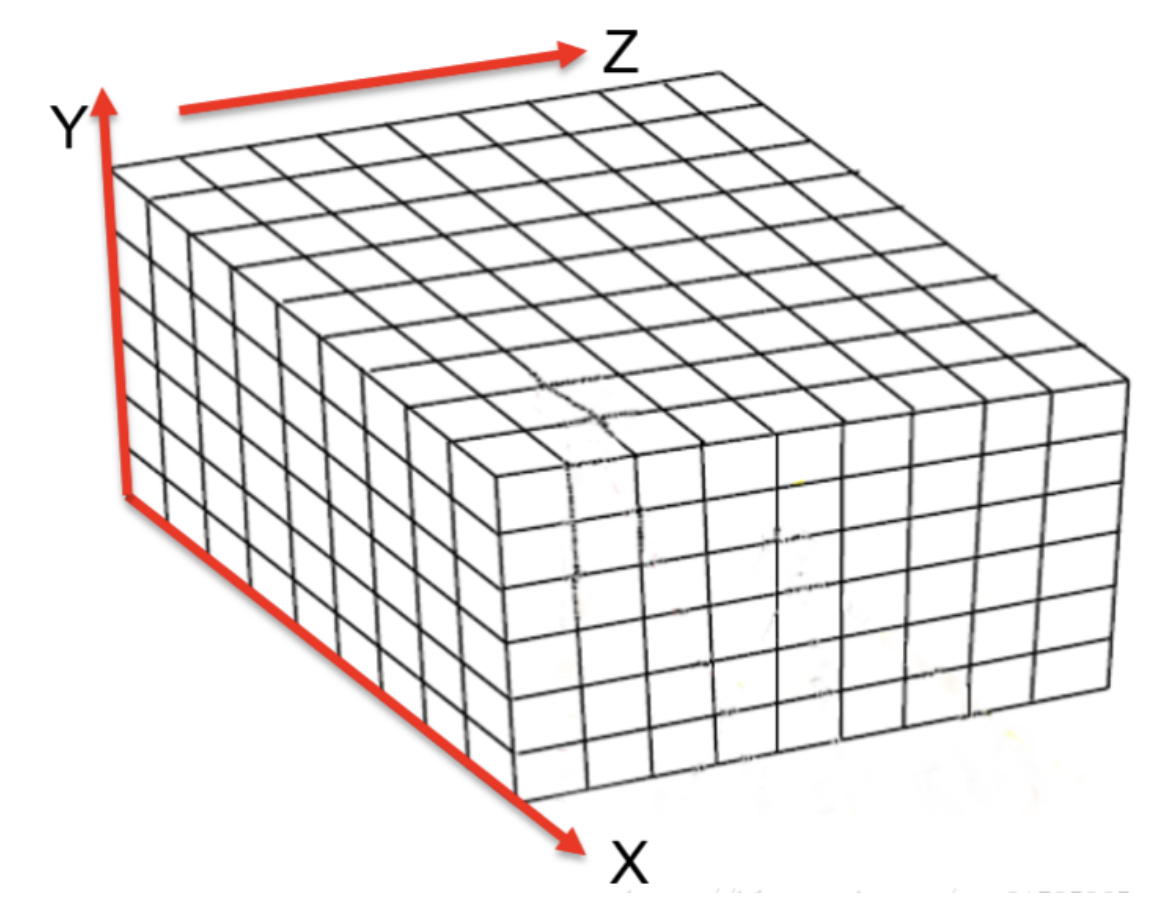
对每个 voxel（记为 $V$）对应空间中的一个点，这个点用两个量来评价：

1. 该 voxel 到最近的 surface（一开始不知道，设为没有）的距离，记为 $T(V)$，即带符号距离；
2. 体素更新时的权重，记为 $W(V)$。

图-2 带符号距离

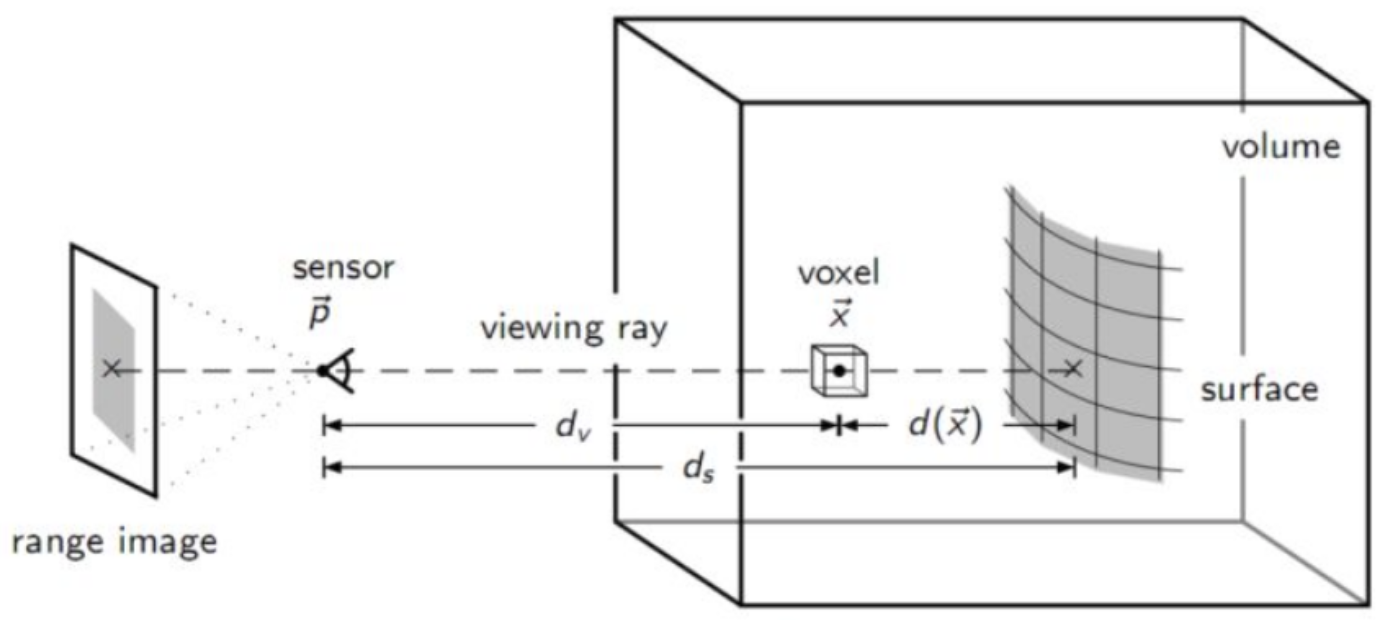
假设真实的平面到相机的深度为 $d_s$，相机采集到的深度为 $d_v$，那么符号距离就是

$d(V) = d_s - d_v$

当 $d(x) > 0$，说明体素在真实面的前面，否则在真实面后面。每次相机采集的数据都认为是最大可能的真实面，也有可能在数据的前后，但是概率要小。这个前后距离可以进行一定限制，如果距离特别远，那么概率会很小，就可以忽略。

1.3 算法步骤

1. 准备：

   • 建立 volume，能够包围要重建的物体；
   • 划分 voxel，其大小取决于 voxel 数目和 volume 的划分；
   • 对于每个 voxel，转化其为世界坐标系下的 3D 位置点 $p$。

2. 遍历所有 voxel，计算 TSDF 值和权重：

   • 由深度数据的相机位姿矩阵，求世界坐标系下点 $p$ 在相机坐标系下的映射点 $v$，并由内参矩阵反投影 $v$ 求深度图像中对应的像素点 $x$，$x$ 的深度值记为 $value(x)$，点 $v$ 到相机坐标原点点距离为 $distance(v)$；

   • $p$ 的 SDF 值为 $sdf(p) = value(x) - distance(v)$，设截断距离为 $u$，则有

     $tsdf(p) = \max (-1, \min(1, {sdf(P) \over u}))$

   • 计算权重：

     $w(p) = {\cos \theta \over distance(v)}$

     其中 $\theta$ 为投影光线与 surface 法向量的夹角。

3. 当前帧与全局融合结果进行融合。

   如果当前帧是第一帧，则第一帧为融合结果；否则需要当前帧与之前的融合结果进行再融合。以 $TSDF(p)$ 为融合 TSDF 值，$W(p)$ 为融合权重，$tsdf(p)$ 为当前帧的 TSDF 值，$w(p)$ 为当前帧的权重值，则更新公式如下：

   $\begin{aligned} TSDF_t (p) &= {W_{t-1} (p) TSDF_{t-1} (p) + w_t (p) tsdf_t (p) \over W_{t-1} (p) + w_t (p)} \\ W_t (p) &= W_{t-1} (p) + w_t (p) \end{aligned}$

每添加一帧深度数据，就执行一遍 2，3 步，直到最后输出结果，给 Marching Cube 计算三角面。

1.4 参考

• https://blog.csdn.net/zfjBIT/article/details/104648505
• https://jijianshu.com/p/fc53c02e9c76
• https://www.guyuehome.com/15664
• https://blog.csdn.net/u011426016/article/details/103239696（源码解析）

2 Marching Cubes Algorithm

2.1 等值面（iso-surface）

等值面是空间中的一个曲面，规定空间中每一个点都有一个属性值，属性值相等的连续空间组成的曲面，称之为等值面。

在采集深度点云时，由于传感器自身精度以及配准的误差在一个地方会采集到很多点，可以认为是对空间连续点的采样，而且点的位置会有很大的波动。通过一些其他方法可以得出这些点与真正的面的差值。那么真正的面在哪？

假如一个点在面的前方，标记为 $+1$，一个点在真实面的后方，标记为 $-1$，可以认为这个真正的面就在这两个点的中间。

还可以这么认为，空间内真正的面会产生一个场，场内有无数个等值面，这个值暂且称之为空间场值，空间场值在面的前方为正值，后方为负值。离真实面越近，空间场值的绝对值越小，真实面的空间场值为 $0$。目的就是在对这个场进行采样后，找到空间内真正的面。

2.2 Marching Cube（MC）算法简介

MC 是 W.Lorensen 等人于 1987 年提出来的一种体素级重建方法。MC 算法也被称为“等值面提取”（Iso-surface Extraction）算法。

2.3 算法思路

Marching Cube 首先将空间分成众多的六面体 cube，类似将空间分成很多的小块。然后找到等值面经过的 cube，如下图：

图-3 cube 示意

求出该 cube 的边与 0 等值面（0 等值面就是空间场值为 0 的等值面）的交点，将这些交点按照一定的拓扑连接关系连接起来，作为 0 等值面在该 cube 中的近似表示。注意是近似表示，采用三角形。

2.3.1 如何找到等值面经过的六面体网格

前面提到，有很多的已知采样点，并且知道这些点在空间中的空间场值，现在我们将空间分为很多个小格子，每个小格子都有 8 个顶点，通过计算 8 个顶点周围（范围与 cube 的大小相关）的采样点，近似计算出 8 个顶点的空间场值（加权平均等方法）。可以对 cube 做以下分类：

• 8 个顶点都没有空间场值，0 等值面不经过或者经过但是没有采样，没有办法进行近似，所以不处理。
• 8 个顶点都有或部分有空间场值，当空间场值都是正值或者都是负值时，说明 0 等值面不在 cube 内。
• 当 cube 的顶点的空间场值有正有负时，则说明有 0 等直面穿过 cube。则需要从众多 cube 内，筛选出这样的 cube。

2.3.2 怎么求 cube 边与 0 等值面的交点

因为 cube 有 8 个顶点，8 个顶点的状态就有 $2^8 = 256$ 种，但是由于 cube 具有对称性，通过对称性，可以简化这些状态至 15 种状态：

图-4 cube 的 15 种状态

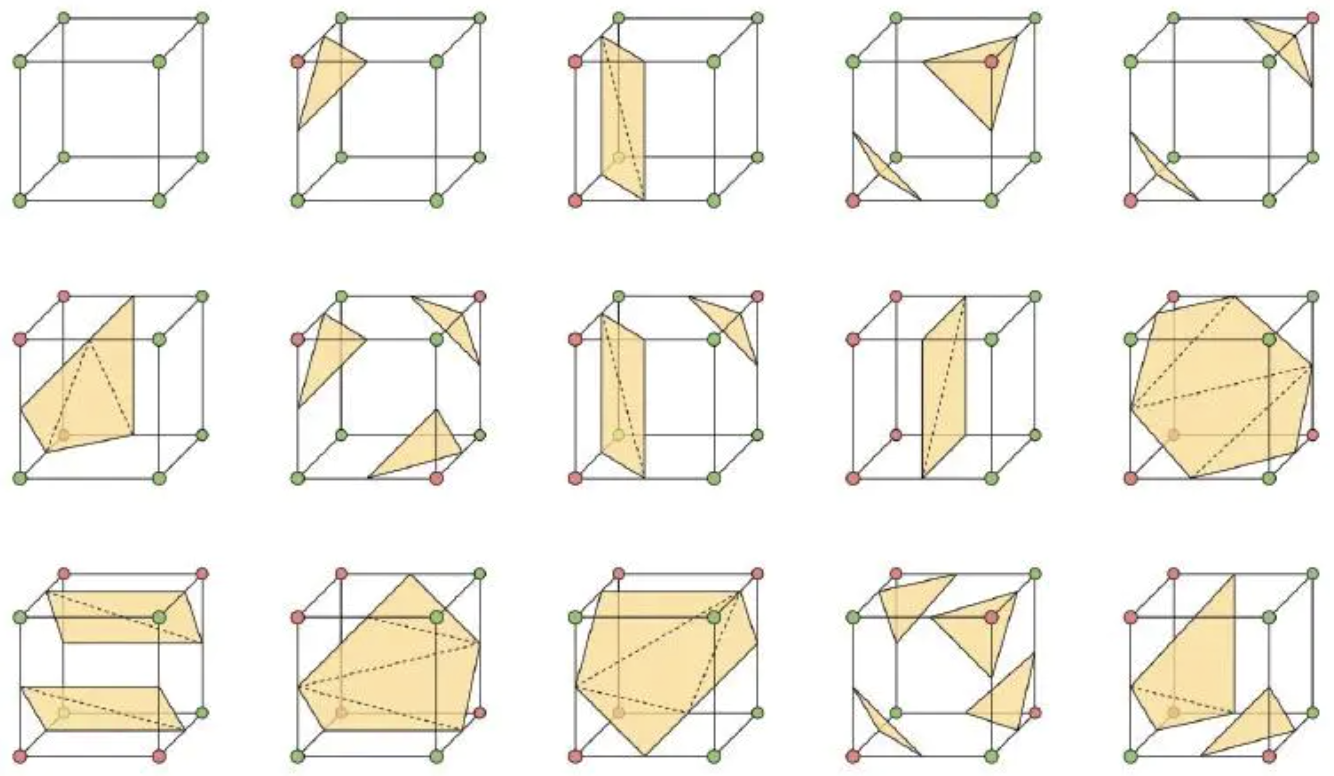
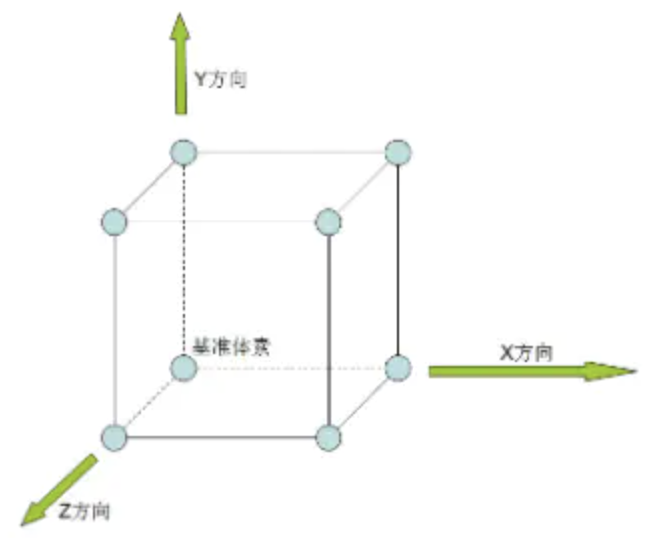
现在需要精算出来这个交点的具体的位置，举一个例子，先给 cube 的所有的顶点和边标记：

图-5 Marching Cube举例-1

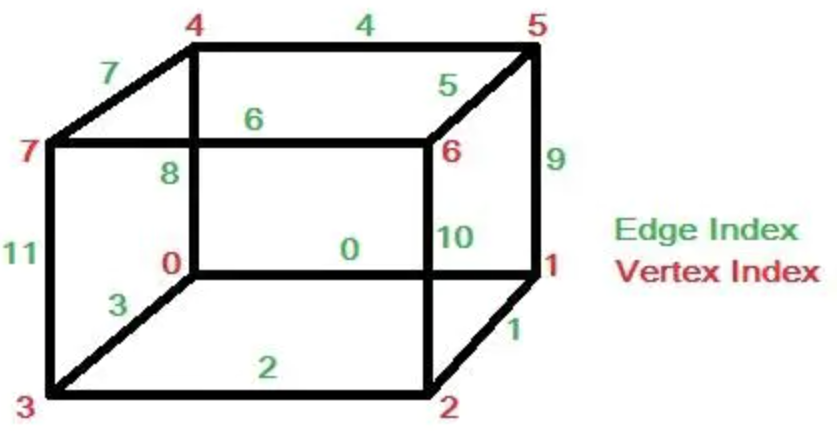
假如体素下方的顶点 3 的值小于等值面值，其他顶点上的值都大于等值面值，那么可以生成一个与体素边 2，3，11 相交的三角面片，而三角面片顶点的具体位置则需要根据等值面值和边顶点 3-2，3-0，3-7 的值线性插值计算得到。

图-6 Marching Cube举例-2

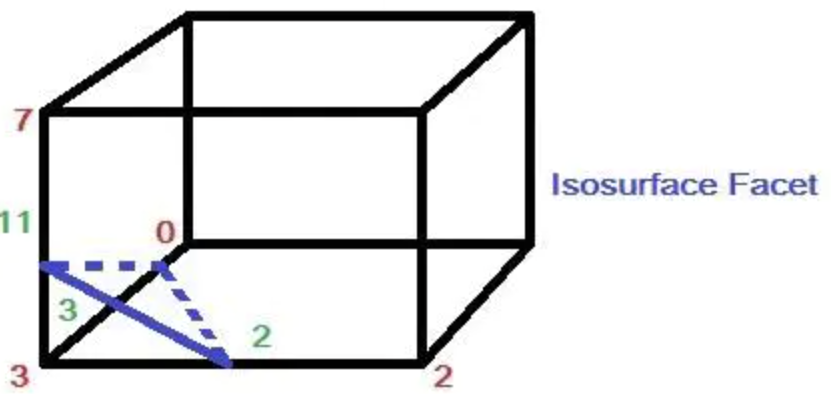
将交点坐标用 $P$ 表示，$P_1$、$P_2$ 代表边上两个端点的坐标，$V_1$、$V_2$ 代表这两个端点上的值，$V$ 代表等值面值，那么交点坐标的计算公式如下（线性插值，也可以是其他方法）：

$P = P_1 + {V - V_1 \over V_2 - V_1} (P_2 - P_1)$

那么现在对所有的含有等值面的 cube 计算出了其与等值面的交点。最后一步，就是将这些交点连接成三角形。

2.3.3 这些交点按照怎么的拓扑连接关系连接，是怎么操作的？

连接三角形的拓扑结构，也在前面 15 中情况中，都画了出来，只要按照上图的表中已经记录好的连接关系，就可以将三角形连接出来。

2.4 算法流程

1. 将原始数据经过预处理之后，读入特定的数组或者八叉树中。

2. 从 volume 中提取一个 cube，成为当前 cube 同时获取该 cube 的所有信息，例如 8 个顶点的值，坐标位置等。

3. 将当前 cube 的 8 个顶点的函数值与给定等值面值 C 进行比较,得到该 cube 的状态表。

4. 根据当前 cube 的状态表索引，找出与等值面相交的 cube 棱边，并采用线性插值的方法计算出各个交点的位置坐标。

5. 利用中心差分法，求出当前 cube 的 8 个顶点的法向量，采用线性插值的方法，得到三角面各个顶点的法向量。

6. 根据各个三角面顶点的坐标、顶点法向量进行三角面的连接。

2.5 参考

• https://www.jianshu.com/p/5a6ade7b77b6
• https://zhuanlan.zhihu.com/p/48022195
• https://zhuanlan.zhihu.com/p/45292978（连接 TSDF 和 Marching Cube）