Upsampling and Subsampled

关于上采样和下采样的理论整理。

上采样和下采样

---

1 上采样

放大图像（上采样（upsampling）或图像插值（interpolating））的主要目的是放大原图像，从而可以显示在更高分辨率的显示设备上。对图像的缩放操作并不能带来更多关于该图像的信息，因此图像的质量将不可避免地受到影响。然而，有的缩放方法能够增加图像的信息，从而使得缩放后的图像质量超过原图质量。

1.1 线性插值

1.1.1 最近邻插值算法

当图片放大时，缺少的像素通过直接使用与之最近原有颜色生成，在待求像素的四邻像素中，将距离待求像素最近的邻灰度赋给待求像素。设待求像素的坐标为 $(i+u,j+v)$，$i,j$ 为正整数，$u,v$ 为大于 0 小于 1 的小数，则待求像素灰度的值 $f(i+u,j+v)$ 的计算方式如下图所示：

图-1 最近邻插值

如果 $(i+u,j+v)$ 落在 A 区域内，即 $u<0.5,v<0.5$，则将 a 点的像素值赋给待求像素，其他三种情况同理。最邻近法计算量较小，但可能会造成插值生成的图像灰度上的不连续，在灰度变化的地方可能出现明显的锯齿状。

1.1.2 双线性插值算法

核心思想是在两个方向分别进行一次线性插值。

1. 先确定变量

   • 四个像素点：$Q_{11},Q_{12},Q_{21},Q_{22}$
   • 像素点坐标：$(x_1,y_1),(x_1,y_2),(x_2,y_1),(x_2,y_2)$
   • 像素值：$f(Q_{11}),f(Q_{12}),f(Q_{21}),f(Q_{22})$
   • 横向插值插入的两个点为 $R_1,R_2$，坐标为 $(x,y_1),(x,y_2)$
   • 纵向插值插入的一个点为 $P$，坐标为 $(x,y)$
   
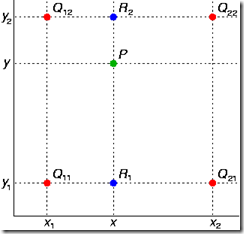
   图-2 双线性插值

2. 插值的目的

   图像扩展，由已知的像素点的值来计算出来原本不存在的像素点。

3. 插值的方法

   • 先横向插，再纵向插
   • 先纵向插，再横向插

4. 计算过程

   • 计算横向插值，由 $Q_{22}$ 和 $Q_{12}$ 计算 $R_2$ 的过程：

     $\frac{f(Q_{22})-f(Q_{12})}{x_2-x_1} \approx \frac{f(Q_{22})-f(R_2)}{x_2-x}$

     交叉相乘并化简，得到：

     $f(R_2)\approx \frac{x_2-x}{x_2-x_1}f(Q_{12})+\frac{x-x_1}{x_2-x_1}f(Q_{22})$

   • 同理，由 $Q_{11}$ 和 $Q_{21}$ 计算 $R_1$：

     $f(R_1)\approx \frac{x_2-x}{x_2-x_1}f(Q_{11})+\frac{x-x_1}{x_2-x_1}f(Q_{21})$

   • 结合 $R_1$ 和 $R_2$ 在 $y$ 方向插值得到 $P$：

     $\frac{f(R_2)-f(R_1)}{y_2-y_1}\approx \frac{f(R_2)-f(P)}{y_2-y}$

     化简得：

     $f(P)\approx \frac{y_2-y}{y_2-y_1}f(R_1)+\frac{y-y_1}{y_2-y_1}f(R_2)$

     将 $f(R_1)$ 和 $f(R_2)$ 带入 $f(P)$ 得到：

     $\begin{aligned} f(P) &\approx \frac{f(Q_{11})}{(x_2-x_1)(y_2-y_1)}(x_2-x)(y_2-y)\\ &+\frac{f(Q_{21})}{(x_2-x_1)(y_2-y_1)}(x-x_1)(y_2-y)\\ &+\frac{f(Q_{12})}{(x_2-x_1)(y_2-y_1)}(x_2-x)(y-y_1)\\ &+\frac{f(Q_{22})}{(x_2-x_1)(y_2-y_1)}(x-x_1)(y-y_1) \end{aligned}$

1.1.3 双三次插值算法

双三次插值算法计算复杂、速度较慢。其并不是通过线性插值，而是通过邻近的 $4\times4\ (=16)$ 个像素做加权。假设原图 A 大小为 $m\times n$，缩放 $K$ 倍后图 B 大小为 $M\times N$，即 $K=M/m$。A 中每个像素点都是已知的，要求出 B 中像素点 $B(X,Y)$ 的值，需先找到 $B(X,Y)$ 在 A 中对应的像素 $A(x,y)$，再根据源图像 A 距离像素 $A(x,y)$ 最近的 16 个像素点作为计算 $A(X,Y)$ 的参数，利用 BiCubic 基函数求出 16 个像素点的权重，再做加权叠加得到 $B(X,Y)$ 的值。

根据比例关系 $x/X=m/M=1/K$，可以得到 $B(X,Y)$ 在 A 中的对应坐标：

$A(x,y)=A(X\cdot \frac{m}{M},Y\cdot \frac{n}{N})=A(\frac{X}{K},\frac{Y}{K})$

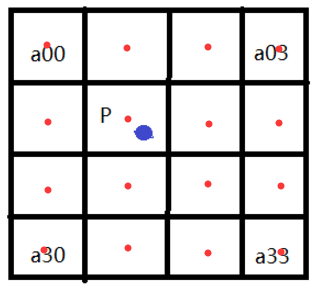
图-3 双三次插值

由于计算出的 $A(x,y)$ 中会出现小数部分，假设 $B(X,Y)$ 在 A 中的对应点记为 $P$（即前面的 $A(x,y)$），则将 $P$ 的坐标记为 $P=(x+u,y+v)$，注意其中 $x,y$ 表示整数部分（蓝点格中红点的像素坐标），$u,v$ 表示小数部分（蓝点到蓝点格中红点的距离）。由此可以得到 $P$ 附近的 16 个像素，将这些像素记为 $a_{ij}\ (i,j=0,1,2,3)$。

构造 BiCubic 函数：

W(x)= \begin{cases} (a+2) \abs{x}^3 + (a+3) \abs{x}^2 + 1,\ &\mathrm{for}\ \abs{x}\le1 \\ a \abs{x}^3 - 5a\abs{x}^2 + 8a\abs{x} - 4a, &\mathrm{for}\ 1<\abs{x}<2 \\ 0, &\mathrm{otherwise} \end{cases}\\ 其中\ a\ 为超参数\mathrm{（可取\ 0.5）}

BiCubic 基函数是一维的，而像素坐标是二维的，因此将像素点的行与列分开计算：BiCubic 中参数 $x$ 表示像素点到 $P$ 的距离，例如 $a_{00}$ 到 $P$ 的距离为 $(1+u,1+v)$，因此 $a_{00}$ 横坐标的权重为 $row_0=W(1+u)$，纵坐标的权重为 $col_0=W(1+v)$，$a_{00}$ 对 $B(X,Y)$ 的贡献为 $a_{00} \times row_0 \times col_0$。从而，$B(X,Y)$ 的像素值为：

$B(X,Y)=\sum_{i=0}^3 \sum_{j=0}^3 a_{ij} \times row_i \times col_j \\ row_0=W(1+u),\ row_1=W(u),\ row_2=W(1-u),\ row_3=W(2-u) \\ col_0=W(1+v),\ col_1=W(v),\ col_2=W(1-v),\ col_3=W(2-v)$

C++ 代码：

#include "opencv2/imgproc/imgproc.hpp"
#include "opencv2/highgui/highgui.hpp"
#include <iostream>
#include <cmath>
#include <fstream>
using namespace cv;
using namespace std;
#define PI 3.14159265
float BiCubicPoly(float x);
void MyScaleBiCubicInter(Mat& src, Mat& dst, float TransMat[3][3]);

int main(int argc, char** argv) {
  // load image
  char* imageName = "images/Lenna_256.png";
  Mat image;
  image = imread(imageName,1);
 
  if (!image.data) {
	  cout << "No image data" << endl;
	  return -1;
  }
  // show image
  namedWindow("image", CV_WINDOW_AUTOSIZE);
  imshow("image", image);  
  Mat dst;
  float transMat[3][3] = {{2.0, 0, 0}, {0, 2.0, 0}, {0, 0, 1}};
 
  MyScaleBiCubicInter(image, dst, transMat);
  namedWindow("out_image", CV_WINDOW_AUTOSIZE);
  imshow("out_image", dst);
  imwrite("Lenna_scale_biCubic2.jpg", dst);
  waitKey(0);
  return 0;
}

float BiCubicPoly(float x) {
	float abs_x = abs(x);
	float a = -0.5;
	if ( abs_x <= 1.0 ) {
		return (a+2)*pow(abs_x,3) - (a+3)*pow(abs_x,2) + 1;
	} else if( abs_x < 2.0 ) {
		return a*pow(abs_x,3) - 5*a*pow(abs_x,2) + 8*a*abs_x - 4*a;
	}
	else
		return 0.0;
}
 
void MyScaleBiCubicInter(Mat& src, Mat& dst, float TransMat[3][3]) {
	CV_Assert(src.data);
	CV_Assert(src.depth() != sizeof(uchar));
	
	// calculate margin point of dst image
	float left =  0;
	float right =  0;
	float top =  0;
	float down =  0;
 
	float x = src.cols * 1.0f;
	float y = 0.0f;
	float u1 = x * TransMat[0][0] + y * TransMat[0][1];
	float v1 = x * TransMat[1][0] + y * TransMat[1][1];
	x = src.cols * 1.0f;
	y = src.rows * 1.0f;
	float u2 = x * TransMat[0][0] + y * TransMat[0][1];
	float v2 = x * TransMat[1][0] + y * TransMat[1][1];
	x = 0.0f;
	y = src.rows * 1.0f;
	float u3 = x * TransMat[0][0] + y * TransMat[0][1];
	float v3 = x * TransMat[1][0] + y * TransMat[1][1];
 
	left =  min( min( min(0.0f,u1), u2 ), u3);
	right =  max( max( max(0.0f,u1), u2 ), u3);
	top =  min( min( min(0.0f,v1), v2 ), v3);
	down =  max( max( max(0.0f,v1), v2 ), v3);
 
	// create dst image
	dst.create(int(abs(right-left)), int(abs(down-top)), src.type());	
 
	CV_Assert(dst.channels() == src.channels());
	int channels = dst.channels();
 
	int i,j;
	uchar* p;
	uchar* q0;
	uchar* q1;
	uchar* q2;
	uchar* q3;
	for (i = 0; i < dst.rows; ++i) {
		p = dst.ptr<uchar>(i);
		for (j = 0; j < dst.cols; ++j) {
			// 
			x = (j+left)/TransMat[0][0]; 
			y = (i+top)/TransMat[1][1];
 
			int x0 = int(x) - 1;
			int y0 = int(y) - 1;
			int x1 = int(x);
			int y1 = int(y);
			int x2 = int(x) + 1;
			int y2 = int(y) + 1;
			int x3 = int(x) + 2;
			int y3 = int(y) + 2;
 
			if ((x0 >= 0) && (x3 < src.cols) && (y0 >= 0) && (y3 < src.rows)) {
				q0 = src.ptr<uchar>(y0);
				q1 = src.ptr<uchar>(y1);
				q2 = src.ptr<uchar>(y2);
				q3 = src.ptr<uchar>(y3);
				
				float dist_x0 = BiCubicPoly(x-x0);
				float dist_x1 = BiCubicPoly(x-x1);
				float dist_x2 = BiCubicPoly(x-x2);
				float dist_x3 = BiCubicPoly(x-x3);
				float dist_y0 = BiCubicPoly(y-y0);
				float dist_y1 = BiCubicPoly(y-y1);
				float dist_y2 = BiCubicPoly(y-y2);
				float dist_y3 = BiCubicPoly(y-y3);
 
				float dist_x0y0 = dist_x0 * dist_y0;
				float dist_x0y1 = dist_x0 * dist_y1;
				float dist_x0y2 = dist_x0 * dist_y2;
				float dist_x0y3 = dist_x0 * dist_y3;
				float dist_x1y0 = dist_x1 * dist_y0;
				float dist_x1y1 = dist_x1 * dist_y1;
				float dist_x1y2 = dist_x1 * dist_y2;
				float dist_x1y3 = dist_x1 * dist_y3;
				float dist_x2y0 = dist_x2 * dist_y0;
				float dist_x2y1 = dist_x2 * dist_y1;
				float dist_x2y2 = dist_x2 * dist_y2;
				float dist_x2y3 = dist_x2 * dist_y3;
				float dist_x3y0 = dist_x3 * dist_y0;
				float dist_x3y1 = dist_x3 * dist_y1;
				float dist_x3y2 = dist_x3 * dist_y2;
				float dist_x3y3 = dist_x3 * dist_y3;
				
				switch (channels) {
					case 1:
						{
							break;
						}
					case 3:
						{
							p[3*j] =    (uchar)(q0[3*x0] * dist_x0y0 +
												q1[3*x0] * dist_x0y1 +
												q2[3*x0] * dist_x0y2 +
												q3[3*x0] * dist_x0y3 +
												q0[3*x1] * dist_x1y0 +
												q1[3*x1] * dist_x1y1 +
												q2[3*x1] * dist_x1y2 +
												q3[3*x1] * dist_x1y3 +
												q0[3*x2] * dist_x2y0 +
												q1[3*x2] * dist_x2y1 +
												q2[3*x2] * dist_x2y2 +
												q3[3*x2] * dist_x2y3 +
												q0[3*x3] * dist_x3y0 +
												q1[3*x3] * dist_x3y1 +
												q2[3*x3] * dist_x3y2 +
												q3[3*x3] * dist_x3y3 ) ;
 
							p[3*j+1] =  (uchar)(q0[3*x0+1] * dist_x0y0 +
												q1[3*x0+1] * dist_x0y1 +
												q2[3*x0+1] * dist_x0y2 +
												q3[3*x0+1] * dist_x0y3 +
												q0[3*x1+1] * dist_x1y0 +
												q1[3*x1+1] * dist_x1y1 +
												q2[3*x1+1] * dist_x1y2 +
												q3[3*x1+1] * dist_x1y3 +
												q0[3*x2+1] * dist_x2y0 +
												q1[3*x2+1] * dist_x2y1 +
												q2[3*x2+1] * dist_x2y2 +
												q3[3*x2+1] * dist_x2y3 +
												q0[3*x3+1] * dist_x3y0 +
												q1[3*x3+1] * dist_x3y1 +
												q2[3*x3+1] * dist_x3y2 +
												q3[3*x3+1] * dist_x3y3 ) ;
 
							p[3*j+2] =  (uchar)(q0[3*x0+2] * dist_x0y0 +
												q1[3*x0+2] * dist_x0y1 +
												q2[3*x0+2] * dist_x0y2 +
												q3[3*x0+2] * dist_x0y3 +
												q0[3*x1+2] * dist_x1y0 +
												q1[3*x1+2] * dist_x1y1 +
												q2[3*x1+2] * dist_x1y2 +
												q3[3*x1+2] * dist_x1y3 +
												q0[3*x2+2] * dist_x2y0 +
												q1[3*x2+2] * dist_x2y1 +
												q2[3*x2+2] * dist_x2y2 +
												q3[3*x2+2] * dist_x2y3 +
												q0[3*x3+2] * dist_x3y0 +
												q1[3*x3+2] * dist_x3y1 +
												q2[3*x3+2] * dist_x3y2 +
												q3[3*x3+2] * dist_x3y3 ) ;
 
							float thre = 198.0f;
							if ((abs(p[3*j]-q1[3*x1]) > thre) || (abs(p[3*j+1]-q1[3*x1+1]) > thre) ||
								(abs(p[3*j+2]-q1[3*x1+2]) > thre)) {
								p[3*j] = q1[3*x1];
								p[3*j+1] = q1[3*x1+1];
								p[3*j+2] = q1[3*x1+2];
							}					
							break;
						}
				}
			}
		}
	}
}

1.2 深度学习

1.2.1 转置卷积（反卷积）

1.2.1.1 正向卷积

假设输入图像 input 的尺寸为 $4\times 4$，元素矩阵为：

$input= \left[ \begin{matrix} x_{1} &x_{2} &x_{3} &x_{4} \\ x_{5} &x_{6} &x_{7} &x_{8} \\ x_{9} &x_{10} &x_{11} &x_{12} \\ x_{13} &x_{14} &x_{15} &x_{16} \end{matrix} \right]$

卷积核 kernel 的尺寸为 $3\times3$，元素矩阵为：

$kernel= \left[ \begin{matrix} w_{0,0} &w_{0,1} &w_{0,2} \\ w_{1,0} &w_{1,1} &w_{1,2} \\ w_{2,0} &w_{2,1} &w_{2,2} \end{matrix} \right]$

设定步长 $stride=1$，填充 $padding=0$，即 $i=4,k=3,s=1,p=0$，按照卷积计算公式，根据 $o=\lfloor\frac{i+2p-k}{s}\rfloor+1$ 得到输出图像尺寸为 $2\times2$。

把 $input$ 展开为一个列向量 $X$：

$X= \left[ \begin{matrix} x_{1} &x_{2} &x_{3} &x_{4} &x_{5} &x_{6} &x_{7} &x_{8} &x_{9} &x_{10} &x_{11} &x_{12} &x_{13} &x_{14} &x_{15} &x_{16} \end{matrix} \right] ^T$

输出图像展开为列向量 $Y$：

$Y= \left[ \begin{matrix} y_{1} &y_{2} &y_{3} &y_{4} \end{matrix} \right] ^T$

对于输入 $X$ 和输出 $Y$，可以用矩阵运算描述为：

$Y=CX$

通过推导，可以得到稀疏矩阵 $C$：

$C= \left[ \begin{matrix} w_{0,0} &w_{0,1} &w_{0,2} &0 &w_{1,0} &w_{1,1} &w_{1,2} &0 &w_{2,0} &w_{2,1} &w_{2,2} &0 &0 &0 &0 &0 \\ 0 &w_{0,0} &w_{0,1} &w_{0,2} &0 &w_{1,0} &w_{1,1} &w_{1,2} &0 &w_{2,0} &w_{2,1} &w_{2,2} &0 &0 &0 &0 \\ 0 &0 &0 &0 &w_{0,0} &w_{0,1} &w_{0,2} &0 &w_{1,0} &w_{1,1} &w_{1,2} &0 &w_{2,0} &w_{2,1} &w_{2,2} &0 \\ 0 &0 &0 &0 &0 &w_{0,0} &w_{0,1} &w_{0,2} &0 &w_{1,0} &w_{1,1} &w_{1,2} &0 &w_{2,0} &w_{2,1} &w_{2,2} \end{matrix} \right]$

反卷积就是要对这个矩阵运算过程进行逆运算，通过 $C$ 和 $Y$ 求 $X$，通过各个矩阵的尺寸大小，可以得到逆运算过程为：

$X=C^TY$

如果代入数字计算会发现，反卷积的操作只是恢复了矩阵 $X$ 的尺寸大小，并不能恢复 $X$ 的每个元素值，只能保证矩阵大小一致。

1.2.1.2 反卷积

记：

$\begin{aligned} o &= output\ size \\ s &= stride \\ i &= input\ size \\ p &= padding \\ k &= kernel\ size \end{aligned}$

卷积的尺寸关系为：

$o=\lfloor\frac{i+2p-k}{s}\rfloor+1$

反卷积的尺寸关系为：

• 若 $(o+xp-k)\mod s=0$：

  $o' = s(i'-1)+k-2p$

• 否则：

  $o' = s(i'-1)+a+k-2p$

实际上卷积和反卷积只是两个有关联的操作，但并不是互为逆运算，仅仅是在形状上存在互逆的关系。

1.2.1.3 反卷积的应用

在 ResNet、GoogleNet 中，最后一层卷积输出的若干特征图尺寸为 $7\times7$，若想通过上采样还原为原始图像的 $224\times224$，则带入公式：

$o=s(i-1)+k-2p,\ \mathrm{where}\ o=224,i=7$

此处取 $(o+2p-k)\mod s=0$，因此可得：

$6s+k-2p=0$

经过实验，可以得到合适的一组取值：

$s=32,\ p=16,\ k=64$

1.2.2 其他基于深度学习的算法

• PixelShuffle
• DUpsampling
• Meta-Upscale
• CAPAFE

1.3 其他上采样算法

• Inverse Distance to a Power（反距离加权插值法）
• Kriging（克里金插值法）
• Minimum Curvature（最小曲率)
• Modified Shepard’s Method（改进谢别德法）
• Natural Neighbor（自然邻点插值法）
• Polynomial Regression（多元回归法）
• Radial Basis Function（径向基函数法）
• Triangulation with Linear Interpolation（线性插值三角网法）
• Moving Average（移动平均法）
• Local Polynomial（局部多项式法）

2 下采样

缩小图像（下采样（subsampled）或降采样（downsampled））的主要目的为：

1. 使得图像符合显示区域的大小
2. 生成对应图像的缩略图

2.1 下采样的实现

• 方法一：for 循环隔行隔列循环遍历每一个像素点

  % 读入图像进行下采样
  clear all;
  close all;
  clc;
  img = imread('...');
  % n为下采样倍数
  n = 2;
  img = rgb2gray(img);
  [h w] = size(img);
  L = 1;
  R = 1;
  % 对图像进行下采样
  img_down = zeros(256,256);
  
  % 方法一循环遍历每一个像素点，j为行，i为列
  for j = 1:n:h
      for i = 1:n:w
          img_down(L, R) = img(j, i);
          R = R+1;
      end
      L = L+1;
      R = 1;
  end

• 方法二：矩阵隔行隔列赋值

  % 方法二矩阵隔行隔列赋值
  img_down = img(1:n:512, 1:n:512);
  imshowpair(img,(uint8(img_down)), 'montage');

  方法二比方法一在计算上会有更高的效率。

2.2 DCT 域采样算法

% 根据 Dugad 方法实现

I = imread('...');
I = rgb2gray(I);
figure(1);
imshow(I);
[width, height] = size(I);
block_size_x = 8;
block_size_y = 8;
x_block_num = width / block_size_x;
y_block_num = height / block_size_y;


z_dst = zeros(width / 2,height / 2);

pfun1 = @dct2;

I_freq = blkproc(I, [8 8], pfun1);

for i = 1: x_block_num
    for j = 1 : y_block_num
        P = I_freq((i-1) * 8 + 1: (i-1) * 8 + 4, (j-1) * 8 + 1: (j-1) * 8 + 4);
        P = P/2.0;
        z_dst((i-1) * 4 + 1: (i-1) * 4 + 4, (j-1) * 4 + 1: (j-1) * 4 + 4) = P;  
    end
 end

pfun2 = @idct2;

J = blkproc(z_dst, [4 4], pfun2);
J = uint8(round(J));
figure(2);
imshow(J);

参考

• https://blog.csdn.net/qq_34919792/article/details/102697817
• https://blog.csdn.net/stf1065716904/article/details/78450997
• https://blog.csdn.net/u013185349/article/details/84529982
• https://blog.csdn.net/gaotihong/article/details/79164172
• https://blog.csdn.net/weixin_42468475/article/details/121948821
• https://blog.csdn.net/Aoman_Hao/article/details/105020112